文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2015)04-0139-05
0 引言
交通系統(tǒng)是城市經(jīng)濟(jì)活動的命脈,也是衡量一個城市文明程度的重要標(biāo)志,同時對城市的經(jīng)濟(jì)發(fā)展和居民生活水平的提高起著極為重要的作用。城市道路交通的擁擠嚴(yán)重影響著居民生活,并造成社會生產(chǎn)力的極大浪費(fèi)。如何有效地緩解交通擁擠,提高交通系統(tǒng)效率,成為世界各國亟待解決的問題。在城市交通網(wǎng)中交通干線承擔(dān)了城市交通的主要負(fù)荷,因此,在不增加道路的前提下,對干線交通燈的智能協(xié)調(diào)控制成為緩解交通壓力的主要手段,也是目前各國學(xué)者研究的重點(diǎn)。如Little等建立了最大綠波帶寬的MAXBAND模型,提出了干線雙向綠波協(xié)調(diào)控制配時策略[1-2];盧凱等利用分析時距的方法,給出了進(jìn)口道單獨(dú)放行條件下的干線雙向綠波協(xié)調(diào)控制數(shù)解算法[3];徐世洪等人基于交通流的動態(tài)模型,提出了一種雙向綠波的干線相鄰路口相位差優(yōu)化控制方法,并應(yīng)用自適應(yīng)遺傳算法進(jìn)行改進(jìn)求解,實(shí)現(xiàn)了交通干線分級遞階協(xié)調(diào)控制[4]。本文依據(jù)干線協(xié)調(diào)控制原理,提出一種基于粒子群算法交通干線控制策略。以車輛行駛過程中延誤時間最小為優(yōu)化目標(biāo)[5],建立交通干線雙向綠波控制延誤模型,并通過該控制策略進(jìn)行優(yōu)化控制。最終通過實(shí)驗結(jié)果對比驗證了該控制策略的有效性。
1 干線總延誤模型的建立
城市干線交通信號的控制參數(shù)有:各交叉口的信號周期、綠信比以及相位差。干線交通信號的協(xié)調(diào)控制就是將干線上若干相鄰交叉路口的信號進(jìn)行協(xié)調(diào)配時,使進(jìn)入交通干線的車隊不遇或少遇紅燈,以達(dá)到減少延誤的目的。
1.1 相位的確定
相位是指在周期時間內(nèi)按需求人為設(shè)定的某個方向上的交通流(或幾個方向上的交通流的組合),同時得到通行權(quán)的時間帶。
干線系統(tǒng)的特點(diǎn)是干線方向車流量遠(yuǎn)遠(yuǎn)大于非干線方向車流量,且車流量以直行車流為主。但在實(shí)際中,即使左轉(zhuǎn)的車流量不大,如果不加以單獨(dú)控制,也會對直行車流產(chǎn)生較大干擾。因此,相位劃分如圖1所示。

1.2 模型的基本假設(shè)
由于交通系統(tǒng)的隨機(jī)性、模糊性和不確定性,延誤模型的建立基于以下基本假設(shè):
(1)相位轉(zhuǎn)換中的黃燈時間通常為2 s,將其歸入相位轉(zhuǎn)換的紅燈和綠燈時長內(nèi),相位轉(zhuǎn)換無時滯;
(2)保持每個信號周期的相位數(shù)和相位放行順序固定不變;
(3)干線控制系統(tǒng)內(nèi)部的交通流為非飽和流;
(4)車輛到達(dá)交叉口看作是點(diǎn)到達(dá);
(5)系統(tǒng)內(nèi)非協(xié)調(diào)相位方向上的車流采用隨機(jī)到達(dá)方式處理,根據(jù)Webster延誤模型計算[6];
(6)系統(tǒng)內(nèi)干線方向上由于交叉口相互間距不宜過大,交通流受上游交叉口信號影響而不再隨機(jī)。
1.3 模型的建立
在干線協(xié)調(diào)控制系統(tǒng)中,設(shè)主干線方向上的相位為協(xié)調(diào)相位,其余方向上的相位設(shè)為非協(xié)調(diào)相位,故車輛延誤分為協(xié)調(diào)相位的延誤和非協(xié)調(diào)相位的延誤兩部分。
若車隊駛向交叉口未受阻,即在綠燈期間可以完全通過,則時間延誤為0。若行駛車隊受阻,則受阻情況分為:車隊在到達(dá)交叉口時第一輛車就遇到紅燈,導(dǎo)致整個車隊全部受阻;在信號變?yōu)榧t燈時車隊已部分通過交叉口,導(dǎo)致車隊局部受阻。
(1)協(xié)調(diào)相位車隊全部受阻延誤模型
干線系統(tǒng)中車輛行駛方向分為上行方向和下行方向,上行車隊從交叉口i到i+1途經(jīng)路長為li,i+1,上行方向的平均車速為vup,車隊第一輛車遇到紅燈的等待時間為tw,up,交叉口i到i+1的相位差是?椎i+1,i。則分析可得:

車隊通過交叉口i+1的通行能力為ui+1,紅燈時長為tred,綠燈時長為tgreen,交叉口疏散累積車輛需tgo,up,在變?yōu)榫G燈之后到達(dá)的車輛不受阻地通過交叉口i+1,則:
qi+1,up(tw,up+tgo,up)=tgo,up·ui+1(2)
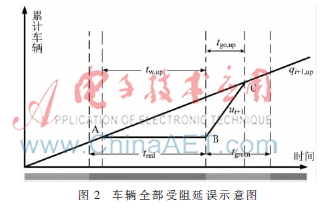
如圖2所示,△ABC的面積即為協(xié)調(diào)相位中上行方向車隊全部受阻的延誤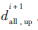 。即:
。即:

在式(3)中,當(dāng)![V2([}D][9N[ZZ9R4M}LHHWR.jpg V2([}D][9N[ZZ9R4M}LHHWR.jpg](http://files.chinaaet.com/images/2015/07/23/6357327762262300009950372.jpg) 時車輛全部受阻。相鄰兩交叉口i與i+1之間的相位差之和為周期C,即i+1,i+i,i+1=C。同理可知,下行方向的車流量全部受阻時協(xié)調(diào)相位延誤為:
時車輛全部受阻。相鄰兩交叉口i與i+1之間的相位差之和為周期C,即i+1,i+i,i+1=C。同理可知,下行方向的車流量全部受阻時協(xié)調(diào)相位延誤為:
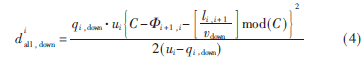
(2)協(xié)調(diào)相位車隊局部受阻延誤模型
當(dāng)mod(C)<i+1,i時,在車隊行駛至交叉口i+1時,一部分車輛無阻礙通過,而余下車輛受阻。受阻車輛等待時間為紅燈時長tred,綠信比為?姿。在受阻過程中,未趕上綠燈的受阻車輛有qi+1,up·tred輛,當(dāng)下一周期綠燈信號到來時需要經(jīng)過t,受阻車輛全部通過交叉口。由此可得:

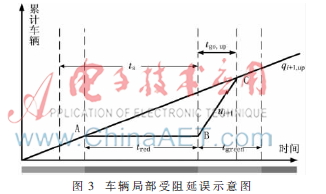
如圖3所示,S△ABC即為協(xié)調(diào)相位方向上車隊上行方向局部受阻的延誤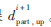 。即:
。即:
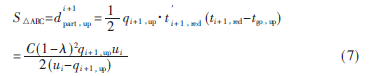
同理可知,下行方向車流量局部受阻時協(xié)調(diào)相位的延誤為:
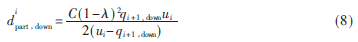
綜上所述,引入變量 ?琢i設(shè)定兩種情況,上行車隊在交叉口處協(xié)調(diào)相位的延誤表達(dá)為:

在式(9)中,如果車輛全部受阻,則取 i=1;如果車輛局部受阻,則取 i=0。
同理,引入變量?茁i設(shè)定下行車隊兩種情況在交叉口處協(xié)調(diào)相位的延誤為:

在式(10)中,如果車輛全部受阻,則取?茁i=1;如果車輛局部受阻,則取i=0。
(3)非協(xié)調(diào)相位車隊延誤
在干線系統(tǒng)中,飽和率小于1,并且非協(xié)調(diào)相位車流隨機(jī)到達(dá),所以可以根據(jù) Webster 延誤模型計算每一輛車的平均延誤:

式中,qi是相位i平均車輛到達(dá)率,單位為輛/時(pcu/h); i為相位i的飽和度。
式(11)中第一部分是均勻車輛所產(chǎn)生的延誤,第二部分是隨機(jī)車輛所產(chǎn)生的延誤,將兩部分求和減去校正部分(通常情況下,校正部分可以忽略),因此,系統(tǒng)中的非協(xié)調(diào)相位的延誤模型為:

式中, qik表示第i個交叉口第k相位的車流量,dik表示第i個交叉口第k相位的車輛平均延誤。
綜上所述,干線系統(tǒng)的總延誤為:

在式(13)中,引入加權(quán)因子?滓,當(dāng)?滓=1時,只考慮協(xié)調(diào)相位的延誤;只考慮非協(xié)調(diào)相位的延誤;當(dāng)(0,1)時,則為同時考慮協(xié)調(diào)相位和非協(xié)調(diào)相位的總延誤。
2 改進(jìn)的粒子群算法干線協(xié)調(diào)優(yōu)化
城市交通信號控制系統(tǒng)是一個典型的多輸入多輸出的復(fù)雜系統(tǒng),必須盡可能將干線協(xié)調(diào)控制參數(shù)同時優(yōu)化。而且,相比其他優(yōu)化方法而言,粒子群算法的速度快,效率高,更適用于干線交通延誤模型優(yōu)化求解。
2.1 基本的粒子群算法
1995年,Eberhart 博士和Kennedy 博士受到飛鳥集群活動的規(guī)律性的啟發(fā),針對鳥群捕食行為的研究提出粒子群算法(PSO)[7]。
PSO優(yōu)化算法的速度公式(14)和位置公式(15)持續(xù)更新如下所示:

式中, 為粒子的速度;w為慣性權(quán)重,通常取值在0.1~0.9之間;
為粒子的速度;w為慣性權(quán)重,通常取值在0.1~0.9之間; 為當(dāng)前粒子的位置;r是介于(0,1)之間的隨機(jī)數(shù);c1,c2為加速常數(shù)。
為當(dāng)前粒子的位置;r是介于(0,1)之間的隨機(jī)數(shù);c1,c2為加速常數(shù)。
2.2 改進(jìn)的粒子群算法
傳統(tǒng)PSO算法收斂速度較其他進(jìn)化算法快,但容易陷入局部極小點(diǎn)。因此,文獻(xiàn)[8]提出一種新的粒子群優(yōu)化算法——?dú)v史最優(yōu)共享的粒子群優(yōu)化算法(VSHBPSO)。VSHBPSO的核心思想:原粒子與一切具有優(yōu)良基因的粒子交互,不斷趨向優(yōu)良,同時粒子的更新還向之前實(shí)驗中搜索的全局歷史最優(yōu)位置學(xué)習(xí)。
基于歷史最優(yōu)共享PSO算法更新位置公式為:
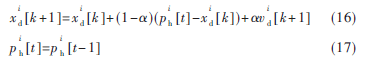
改進(jìn)的PSO算法采用十局運(yùn)行機(jī)制:每一次實(shí)驗結(jié)束所得全局最優(yōu)解應(yīng)用在下一次運(yùn)算過程中,以此類推,取最終得到的最優(yōu)解。
2.3 算法實(shí)現(xiàn)步驟
根據(jù)以上分析,改進(jìn)的歷史最優(yōu)共享的粒子群算法的實(shí)現(xiàn)步驟為:
(1)設(shè)置算法的參數(shù)和最大迭代次數(shù),初始化種群X(k)使每個粒子m產(chǎn)生初始速度組成V(k)。
(2)計算種群在搜索空間中每一維的適應(yīng)值。
(3)將粒子當(dāng)前適應(yīng)值與自身的歷史最優(yōu)值和種群歷史最優(yōu)值分別進(jìn)行比較,如果p的值不如當(dāng)前值,則置當(dāng)前值為空間內(nèi)自身的歷史最優(yōu)解;如果p的值不如當(dāng)前值,則置當(dāng)前值為空間內(nèi)種群的歷史最優(yōu)解。
(4)按照速度更新式(14)和位置更新式(16)、(17)對粒子的速度和位置進(jìn)行更新,并形成新的種群X(k+1)。
(5)查看是否符合算法結(jié)束條件,如果符合則算法結(jié)束,求得最優(yōu)解;否則,迭代數(shù)加1,即t=t+1,并跳轉(zhuǎn)至步驟(2)。
3 仿真實(shí)驗研究
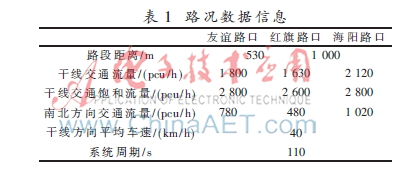
為驗證所建立的模型的有效性,利用秦皇島市河北大街中段車流量較大的3個交叉口(友誼路路口、紅旗路路口和海陽路路口)作為仿真實(shí)驗對象。
3.1 實(shí)驗路段數(shù)據(jù)統(tǒng)計

統(tǒng)計實(shí)驗路段各交叉口一天內(nèi)的車流量并繪制曲線圖,如圖4所示為友誼路口的車流飽和度。
在圖4中可以看出,一天中的車流量飽和度均呈現(xiàn)為小于0.9的非飽和狀態(tài),理論上適用于雙向綠波協(xié)調(diào)控制。而早晨上班時段和下午下班時段屬于高峰期,白天時段車流量屬于平峰期,晚上23點(diǎn)以后至次日清晨車流量較低。
實(shí)驗路段的路況信息如表1所示。
3.2 參數(shù)設(shè)定
優(yōu)化目標(biāo)函數(shù)可以描述為使式(18)中總延誤D獲得最小值的最優(yōu)控制方案:

選取3個交叉口中最大的周期作為系統(tǒng)周期。定義粒子種群 ,設(shè)定種群規(guī)模為n=50的5維粒子群,學(xué)習(xí)因子c1=c2=2,慣性權(quán)重w為0.9~0.4線性下降,最大迭代次數(shù)為100。
,設(shè)定種群規(guī)模為n=50的5維粒子群,學(xué)習(xí)因子c1=c2=2,慣性權(quán)重w為0.9~0.4線性下降,最大迭代次數(shù)為100。
3.3 結(jié)果分析
以路段的平峰時期流量為例進(jìn)行分析。
(1)當(dāng)協(xié)調(diào)相位車流量遠(yuǎn)遠(yuǎn)大于非協(xié)調(diào)相位時,即只考慮協(xié)調(diào)相位的主干線雙向綠波控制,實(shí)驗結(jié)果如表2所示。
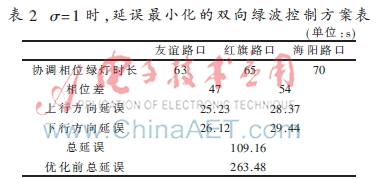
由實(shí)驗結(jié)果可知,在相同路段條件下,采用延誤最小控制方案可以大大減小延誤時間,有效提升通行效率。
(2)當(dāng)協(xié)調(diào)相位和非協(xié)調(diào)相位交通流量均考慮時,協(xié)調(diào)相位延誤的權(quán)值占總延誤權(quán)值的 3/4,支路延誤權(quán)值占總延誤權(quán)值的 1/4,實(shí)驗結(jié)果如表3所示,時距圖如圖5所示。
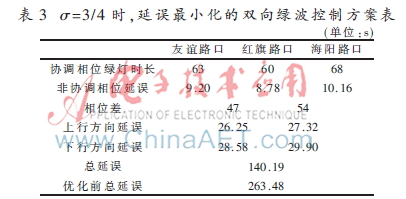

非協(xié)調(diào)相位上的車流在綠燈時間內(nèi)可以通過交叉口,因此考慮非協(xié)調(diào)相位延誤通行效果明顯優(yōu)于傳統(tǒng)定時控制方案。
用此方案進(jìn)行10個周期的仿真實(shí)驗,并與傳統(tǒng)定時控制方案中的延誤對比,如圖6所示。

由此可見,優(yōu)化后的最小延誤控制方案能夠減小約41.3%的時間延誤,有效地提高了城市交通干線的通行效率。
4 結(jié)論
本文在常態(tài)交通情況下建立了干線總延誤模型,并以總延誤最小為優(yōu)化目標(biāo),協(xié)調(diào)綠信比和相位差來實(shí)現(xiàn)交通干線雙向綠波控制。在所建立的模型中考慮非協(xié)調(diào)相位對主干線車流的影響,并引入加權(quán)系數(shù)更合理地展現(xiàn)實(shí)際路況;實(shí)驗部分對城市交通干線進(jìn)行實(shí)地調(diào)查,獲得更符合實(shí)際交通情況的干線數(shù)據(jù);通過將實(shí)際數(shù)據(jù)代入模型進(jìn)行仿真實(shí)驗,驗證了此種控制策略的有效性,對改善城市交通擁堵情況具有積極的現(xiàn)實(shí)意義。
參考文獻(xiàn)
[1] LITTLE J D C.The synchronization of traffic signals by mixed-integer linear programming[J].Operations Research,1966,14(4):568-594.
[2] LITTLE J D C,KELSON M D,GARTNER N H.MAXBAND:a versatile program for setting signals on arteries and trian-gular networks[R].Cambridge: Massachusetts Institute of Technology,1981,12(3):134-141.
[3] 盧凱,徐建閩,李軼舜.進(jìn)口單獨(dú)放行方式下的干道雙向綠波協(xié)調(diào)控制數(shù)解算法[J].中國公路學(xué)報,2010,23(3):95-101.
[4] 徐世洪,李志敏,戴高,等.基于自適應(yīng)遺傳算法的相位差優(yōu)化模型研究[J].交通信息與安全,2011,29(2):13-18.
[5] 沈國江,許衛(wèi)明.交通干線動態(tài)雙向綠波帶控制技術(shù)研究[J].浙江大學(xué)學(xué)報,2008,42(9):1625-1630.
[6] 趙雨旸,馮雨芹,楊忠良.信號交叉口Webster法延誤計算修正模型[J].黑龍江工程學(xué)院學(xué)報:自然科學(xué)版,2010,24(2):8-11.
[7] EBERHART R,KENNEDY J.A new optimizer using parti-cle swarm theory[C].IEEE Proceedings of the 6th Interna-tional Sympo-sium on Micro Machine and Human Science.Piscataway:IEEE Service Center,1995:39-43.
[8] 林蔚天.改進(jìn)的粒子群優(yōu)化算法研究[D].上海:華東理工大學(xué),2012.

