文獻標識碼: A
文章編號: 0258-7998(2015)03-0105-02
0 引言
衛(wèi)星任務設計過程中,如何實現(xiàn)對地面的特定位置和區(qū)域的有效覆蓋是一個關鍵因素。隨著衛(wèi)星通信技術的發(fā)展,衛(wèi)星點波束區(qū)域覆蓋計算方法研究也取得了一定進展[1-3]。當衛(wèi)星工作在正視模式下,波束中心與地面的交點與星下點重合,因此覆蓋邊界是衛(wèi)星波束圓錐與地面的交線[2-3]。當有效載荷工作在側(cè)擺狀態(tài)時,需要對上述模型進行修正。一種模型是假設衛(wèi)星側(cè)視時在地面的投影是一個橢圓,橢圓長短軸和波束寬度以及波束中心星下偏移角?濁有關[4]。但因為地球表面為弧形,實際覆蓋邊緣不是規(guī)則的橢圓曲線,波束中心也并不是位于橢圓中心,因此這種假設誤差較大。
本文中提出一種改進方法,通過衛(wèi)星的側(cè)視角度確定圓錐面,利用站心坐標系中波束的旋轉(zhuǎn)角確定唯一的圓錐母線作為波束中心線,進而得到衛(wèi)星波束中心與地球的交點,最終確定衛(wèi)星覆蓋范圍。
1 側(cè)擺載荷的波束與地面目標的關系
如圖1所示,地球衛(wèi)星位于S點,星下點位于G點, 衛(wèi)星的點波束中心與地球表面相交于E點,其經(jīng)度、緯度坐標分別表示為(Ls,Bs),(Lg,Bg),(Le,Be)。
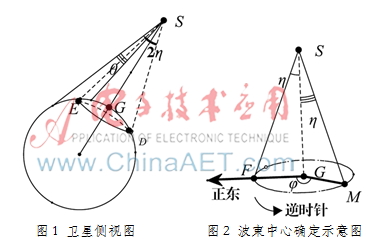
為了確定波束中心SE的方向,建立以星下點為原點的站心坐標系,正東方向(即與X軸平行的方向)所在平面SGF為參考平面,定義波束中心所在平面SGM(E為直線SM上一點)沿逆時針方向偏移MGF的角度為波束中心的旋轉(zhuǎn)角度?漬,波束中心線SM(或者SE)偏離SG的角度為?濁,F(xiàn)、M為以點G為圓心,Re為半徑圓上的點,如圖2所示。其中:

則點F的站心坐標可表示為:
xgf=Re
ygf=0
zgf=0(2)
利用地固坐標系和站心坐標系的轉(zhuǎn)換關系[6],可得地固坐標為(xef,yef,zef):
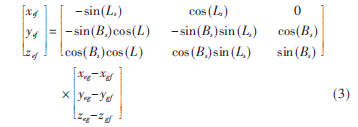
由衛(wèi)星的經(jīng)緯度可以得到星下點G的地固坐標(xeg,yeg,zeg)為:
xeg=Ncos(Bs)cos(Ls)
yeg=Ncos(Bs)sin(Ls)
zeg=Nsin(Bs)(4)
其中N表示零高程地球面半徑。
此時可得到地固坐標系下星下點正東方向的向量GF:
GF=(xef-xeg,yef-yeg,zef-zeg)(5)
并將其作為衛(wèi)星波束中心的偏移角度的參照。
2 載荷側(cè)擺條件下覆蓋范圍求解算法
2.1 波束中心向量SM確定
如果點M在以點G為原點的站心坐標系內(nèi)的坐標表示為(xgm,ygm,zgm),則:
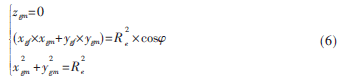
為了用角度得到唯一確定的M點,結(jié)合向量GF和GM外積n=GF×GM判別:即當?漬∈(0°,180°),n與站心坐標系的z軸同向,當?漬∈(180°,360°)時,與z軸反向,從而剔除與GF沿順時針方向夾角為?漬的點M。得到確定的M點站心坐標后,將其轉(zhuǎn)換成地固坐標(xem,yem,zem)。
2.2 確定波束中心點E
由點衛(wèi)星經(jīng)緯度,高度可以得到衛(wèi)星在地固坐標系中坐標(xs,ys,zs),進而可得母線SM的參數(shù)方程:
x=xs+m(xem-xs)
y=ys+m(yem-ys)
z=zs+m(zem-zs)(7)
若把地球表示成一個平均半徑為r0的標準球體,在地固坐標系中,點E的坐標表示為(xe,ye,ze),則:

將式(7)帶入式(8)可得:
a2 m2+2a1 m+a0=0(9)
其中:
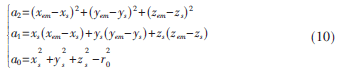
可解得:

為保證式(11)是實數(shù)解,要求星下偏移角?濁要小于地球半徑角?籽。其中:

為了保證波束中心點和衛(wèi)星是在地球的同一側(cè),所以上式中取m的較小值,最終可以得出波束中心點的坐標。將此計算結(jié)果轉(zhuǎn)換為大地坐標系,即可得到衛(wèi)星波束中心在地球表面的位置E(Le,Be,0)。
2.3 覆蓋區(qū)域邊緣點求解
在側(cè)擺條件下,覆蓋范圍的邊緣為不規(guī)則圖形,按照上述求解點波束中心的方法,基于求解出的點波束中心,可以完成對邊緣點的求解,最后完成對覆蓋區(qū)域的計算。
3 仿真分析

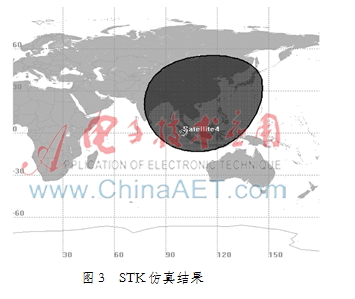

表1中列出了仿真的詳細參數(shù)。圖3是STK軟件覆蓋區(qū)域的仿真結(jié)果[9-10],圖4是該算法通過MATLAB實現(xiàn)的區(qū)域覆蓋仿真。圖3與圖4對比,說明該算法是有效的。
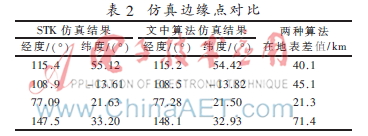
表2為分別選取上、下、左、右四個邊界點進行的對比。數(shù)據(jù)對比表明,本文中提出的算法誤差較小,在地表距離差值在72 km范圍內(nèi)。
4 結(jié)論
本文提出的波束中心確定算法,利用衛(wèi)星旋轉(zhuǎn)角度和斜視角度,通過簡單的幾何關系,最終確定衛(wèi)星波束中心和地球的交點,從而確定衛(wèi)星覆蓋區(qū)域。這種算法簡單,計算速度快、準確度高。因為波束形狀的不同和波束中心點確定無關,所以此算法不僅僅適用于求解點波束的波束中心點,也適用于多種形狀波束的波束中心點計算。
參考文獻
[1] 徐慨,鮑凱,何愛林.衛(wèi)星通信點波束覆蓋算法研究[J].艦船電子對抗,2013,36(2):66-68.
[2] 李德治,宴朝陣,呂波.衛(wèi)星點波束覆蓋區(qū)域算法研究[J].載人航天,2009,15(4).
[3] 樊鵬山,熊偉,李智.載荷側(cè)擺情況下衛(wèi)星覆蓋區(qū)域計算方法研究[C].2009系統(tǒng)仿真技術及其應用學術會議論文集,2009.
[4] 袁孝康.星載合成孔徑雷達導論[M].北京:國防工業(yè)出版社,2003:42-44 .
[5] 白萌,李大林,陳夢云.衛(wèi)星對地覆蓋區(qū)域的融合算法研究[C].第二十三屆全國空間探測學術交流會論文摘要集,2010.
[6] 郭福成,樊昀,周一宇,等.空間電子偵察定位原理[M].北京:國防工業(yè)出版社,2012:33-40.
[7] 翁慧慧.遙感衛(wèi)星對地覆蓋分析與仿真[D].鄭州:信息工程大學,2006.
[8] 劉偉,孟新,胡鈦.衛(wèi)星對地覆蓋的若干問題討論[C].中國空間科學學會空間探測專業(yè)委員會第十八次學術會議論文集(下冊),2005:370-372.
[9] 丁溯泉.STK在航天任務仿真分析中的應用[M].北京:國 防工業(yè)出版社,2011.
[10] 楊穎,王琦.STK在計算機仿真中的應用[M].北京:國防工業(yè)出版社,2005.

