文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào): 0258-7998(2015)05-0145-04
0 引言
近年來(lái),隨著互聯(lián)網(wǎng)和Web技術(shù)的不斷革新,影響最大化問(wèn)題作為社會(huì)網(wǎng)絡(luò)分析領(lǐng)域的重要問(wèn)題得到了快速發(fā)展,并已引起越來(lái)越多的學(xué)者關(guān)注。Li等[1]研究了基于位置感知的影響力最大化問(wèn)題,通過(guò)用戶影響力的上界選擇種子節(jié)點(diǎn)并消除不重要的節(jié)點(diǎn),減少了初始種子節(jié)點(diǎn)的選擇范圍。Kim等[2]基于IC模型將獨(dú)立影響路徑作為影響評(píng)估單元,但是算法未考慮不同節(jié)點(diǎn)影響力的相關(guān)性。Zhao等[3]提出基于網(wǎng)絡(luò)社區(qū)結(jié)構(gòu)的節(jié)點(diǎn)影響力度量策略,但是算法未考慮節(jié)點(diǎn)度在信息傳播中的重要性。Jung等[4]提出了基于IC擴(kuò)展模型的IRIE算法。Guo等[5]提出基于個(gè)性化的影響力最大化算法,對(duì)給定目標(biāo)用戶,尋找對(duì)該目標(biāo)用戶影響力最大的節(jié)點(diǎn)。Cao等[6]提出動(dòng)態(tài)規(guī)劃算法(OASNET)解決影響力最大化,但此算法沒(méi)有考慮社區(qū)間的連通性。Tian等[7]提出結(jié)合啟發(fā)算法和貪心算法的影響力最大化算法HPG,但算法在啟發(fā)階段僅以節(jié)點(diǎn)的度計(jì)算潛在影響力,沒(méi)有充分考慮節(jié)點(diǎn)的其他屬性。與上述研究不同,本文將社區(qū)間的邊界節(jié)點(diǎn)作為初始種子節(jié)點(diǎn)集的候選集,以減少社區(qū)內(nèi)大量非邊界點(diǎn)的計(jì)算時(shí)間,提高運(yùn)行效率。同時(shí),傳統(tǒng)以節(jié)點(diǎn)度的倒數(shù)衡量節(jié)點(diǎn)間影響力忽略了鄰居節(jié)點(diǎn)對(duì)節(jié)點(diǎn)影響的差異,基于此本文綜合考慮邊界節(jié)點(diǎn)的度、所連社區(qū)數(shù)、所連社區(qū)規(guī)模均值3個(gè)因素衡量節(jié)點(diǎn)對(duì)鄰居的影響力傳播的重要性,以更準(zhǔn)確衡量節(jié)點(diǎn)影響力。
1 基于社區(qū)度的邊界節(jié)點(diǎn)影響力最大化算法
本文提出的基于社區(qū)度的邊界節(jié)點(diǎn)影響力最大化算法(CDEA)建立在具有社區(qū)結(jié)構(gòu)的社會(huì)網(wǎng)絡(luò)基礎(chǔ)上,利用HPG算法框架實(shí)施。CDEA算法將社區(qū)連接邊的兩端節(jié)點(diǎn)作為邊界節(jié)點(diǎn),從邊界節(jié)點(diǎn)集中選擇初始傳播種子節(jié)點(diǎn),通過(guò)LT模型在社會(huì)網(wǎng)絡(luò)中傳播,使初始種子節(jié)點(diǎn)產(chǎn)生的影響范圍最大。CDEA算法從邊界節(jié)點(diǎn)集中選擇初始種子節(jié)點(diǎn)是由于在具有社區(qū)結(jié)構(gòu)的社會(huì)網(wǎng)絡(luò)中,跨社區(qū)的信息最大化傳播往往更有現(xiàn)實(shí)意義,而邊界節(jié)點(diǎn)是社區(qū)間信息交流的大使,跨社區(qū)的信息傳播必然會(huì)經(jīng)過(guò)社區(qū)邊界節(jié)點(diǎn),因此可以先不考慮社區(qū)內(nèi)大量的非邊界節(jié)點(diǎn),只考慮少量的邊界節(jié)點(diǎn),可極大降低算法運(yùn)行時(shí)間。同時(shí)CDEA算法用邊界節(jié)點(diǎn)的度和與邊界節(jié)點(diǎn)直接相連的社區(qū)數(shù)以及社區(qū)規(guī)模均值綜合衡量節(jié)點(diǎn)的潛在影響力,提高計(jì)算節(jié)點(diǎn)在貪心階段被快速激活的可能性。
1.1 節(jié)點(diǎn)社區(qū)度
節(jié)點(diǎn)社區(qū)度是指邊界節(jié)點(diǎn)的度、與邊界節(jié)點(diǎn)直接連接的社區(qū)數(shù)、直接相連的社區(qū)規(guī)模均值三者疊加。社區(qū)度既考慮節(jié)點(diǎn)度,也結(jié)合節(jié)點(diǎn)在社會(huì)網(wǎng)絡(luò)中的位置和連通性,可以較好地評(píng)估節(jié)點(diǎn)對(duì)影響力傳播的重要性。

定義1 (社區(qū)度)社區(qū)度主要用于衡量邊界節(jié)點(diǎn)在影響力傳播中的重要性。社區(qū)度是節(jié)點(diǎn)在社區(qū)中鄰居數(shù)、與節(jié)點(diǎn)直接相連的社區(qū)數(shù)以及所連社區(qū)規(guī)模均值的疊加和。節(jié)點(diǎn)在社區(qū)中的鄰居數(shù)越多,表明節(jié)點(diǎn)在社區(qū)中越重要,對(duì)其他節(jié)點(diǎn)產(chǎn)生影響的可能更大。節(jié)點(diǎn)直接相連的社區(qū)數(shù)越多,說(shuō)明節(jié)點(diǎn)與其他社區(qū)產(chǎn)生交流的機(jī)會(huì)越大,對(duì)信息的廣泛傳播具有重要意義。而所連社區(qū)規(guī)模的大小將直接影響信息能否通過(guò)所連社區(qū)繼續(xù)向下一個(gè)社區(qū)擴(kuò)散,所連社區(qū)規(guī)模越大,則此社區(qū)在整個(gè)社會(huì)網(wǎng)絡(luò)中對(duì)信息的快速傳播作用越大。因此采用三者的疊加和可以突出節(jié)點(diǎn)在信息傳播中的重要性。社區(qū)度CDeg(u)定義如下:

社區(qū)規(guī)模均值可縮小,因?yàn)猷従由鐓^(qū)數(shù)少而鄰居社區(qū)節(jié)點(diǎn)數(shù)多或鄰居社區(qū)多而鄰居社區(qū)節(jié)點(diǎn)數(shù)少所造成的差異能更好地平衡社區(qū)數(shù)和每個(gè)社區(qū)規(guī)模間的關(guān)系,因此綜合考慮與節(jié)點(diǎn)直接相連的鄰居社區(qū)以及相應(yīng)社區(qū)規(guī)模均值,可更準(zhǔn)確描述社區(qū)度,提高節(jié)點(diǎn)獲取潛在影響力節(jié)點(diǎn)的精度。
1.2 節(jié)點(diǎn)影響概率
本文綜合邊的權(quán)重和節(jié)點(diǎn)間的交流頻度計(jì)算節(jié)點(diǎn)間的影響概率,更有效地度量節(jié)點(diǎn)間相互影響的概率。影響概率即為節(jié)點(diǎn)激活鄰居的可能性,當(dāng)節(jié)點(diǎn)的所有已激活鄰居對(duì)其影響概率和大于等于特定的閾值θ,則節(jié)點(diǎn)被激活。本文定義節(jié)點(diǎn)u對(duì)鄰居節(jié)點(diǎn)v的影響概率為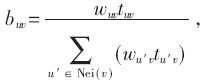 其中tuv為社會(huì)網(wǎng)絡(luò)G中節(jié)點(diǎn)u和v信息交流頻度,wuv為節(jié)點(diǎn)u到v的邊權(quán)重值,Nei(v)表示節(jié)點(diǎn)v的鄰居節(jié)點(diǎn)集。
其中tuv為社會(huì)網(wǎng)絡(luò)G中節(jié)點(diǎn)u和v信息交流頻度,wuv為節(jié)點(diǎn)u到v的邊權(quán)重值,Nei(v)表示節(jié)點(diǎn)v的鄰居節(jié)點(diǎn)集。
1.3 CDEA算法框架
社區(qū)度描述了邊界節(jié)點(diǎn)在整個(gè)網(wǎng)絡(luò)中的拓?fù)浣Y(jié)構(gòu)和重要性,與傳統(tǒng)單一采用節(jié)點(diǎn)度描述節(jié)點(diǎn)與鄰居的關(guān)聯(lián)度相比,可更好地衡量節(jié)點(diǎn)潛在影響力。本文對(duì)HPG算法改進(jìn),基于社區(qū)度提出新的混合算法CDEA。CDEA算法分為啟發(fā)階段和貪心階段。
基于LT傳播模型的影響累積特性在啟發(fā)階段對(duì)邊界節(jié)點(diǎn)啟發(fā)式尋找最有影響力的k′個(gè)節(jié)點(diǎn)作為種子節(jié)點(diǎn)。這些節(jié)點(diǎn)不是局部影響力最大的節(jié)點(diǎn),但是其潛在影響力在后續(xù)信息傳播激活過(guò)程中將會(huì)被充分挖掘,最終獲得比KK算法更大的影響范圍。令inf(u)為節(jié)點(diǎn)u對(duì)所有未被激活鄰居節(jié)點(diǎn)的影響力之和,則:

這里CDeg(u)表示節(jié)點(diǎn)u的社區(qū)度,Nei(u)表示節(jié)點(diǎn)u的鄰居節(jié)點(diǎn)集合,A(u)表示節(jié)點(diǎn)u的鄰居中未被激活的節(jié)點(diǎn)集。PI綜合考慮了節(jié)點(diǎn)的社區(qū)度和對(duì)鄰居中未激活節(jié)點(diǎn)的影響范圍。啟發(fā)階段從未激活的節(jié)點(diǎn)中選擇潛在影響力最大的節(jié)點(diǎn),并將其加入初始集合,直到出現(xiàn)k1個(gè)已經(jīng)被激活的節(jié)點(diǎn)。貪心階段基于LT信息傳播模型,應(yīng)用KK算法不斷計(jì)算邊際影響收益,在局部最優(yōu)的情況下獲取k-k1個(gè)最有影響力的節(jié)點(diǎn)。
CDEA算法具體步驟如下:
輸入:社會(huì)網(wǎng)絡(luò)G=(V,E,W)={C1,C2,C3,…,CM},閾值θ,啟發(fā)因子c,初始集合大小k。
輸出:大小為k的目標(biāo)節(jié)點(diǎn)集S,最終激活節(jié)點(diǎn)數(shù)k0,啟發(fā)階段激活節(jié)點(diǎn)數(shù)k1,貪心階段激活節(jié)點(diǎn)數(shù)k2。

1.4 CDEA算法復(fù)雜度分析
啟發(fā)階段,由于靜態(tài)社會(huì)網(wǎng)絡(luò)中式(2)中節(jié)點(diǎn)社區(qū)度是固定的,并且只需要計(jì)算社區(qū)間的邊界節(jié)點(diǎn)的社區(qū)度,而非整個(gè)網(wǎng)絡(luò)中所有節(jié)點(diǎn),且inf(u)是基于前一個(gè)初始種子節(jié)點(diǎn)并更新整個(gè)網(wǎng)絡(luò)后確定,基本不耗時(shí)間,因此時(shí)間復(fù)雜度為O(C)。同時(shí)啟發(fā)階段不但獲取了大量具有潛在影響力的節(jié)點(diǎn),而且也激活了大量節(jié)點(diǎn)。貪心階段,由于有大量節(jié)點(diǎn)已被激活,未激活節(jié)點(diǎn)比初始狀態(tài)下需要激活節(jié)點(diǎn)數(shù)減少了大部分,即可看作KK算法運(yùn)行在小規(guī)模數(shù)據(jù)集,因此算法復(fù)雜度比KK小。
KK、HPG以及CDEA算法不同階段的時(shí)間復(fù)雜度如表1所示。其中Q1、Q2分別表示啟發(fā)階段CDEA算法和HPG算法每個(gè)種子節(jié)點(diǎn)的平均激活節(jié)點(diǎn)數(shù)。T1、T2、T3分別表示貪心階段CDEA算法、HPG算法、KK算法每個(gè)種子的平均激活范圍。N、M、M′分別表示社會(huì)網(wǎng)絡(luò)G的節(jié)點(diǎn)數(shù)、邊數(shù)、社區(qū)邊界節(jié)點(diǎn)數(shù)。M′<<M<<N,因此可推斷CDEA算法比LPG算法、KK算法時(shí)間復(fù)雜度低很多。

2 實(shí)驗(yàn)
本文實(shí)驗(yàn)中線性閾值模型中的每個(gè)節(jié)點(diǎn)閾值?茲取固定值0.5,啟發(fā)因子c用于平衡不同階段的步數(shù),其中啟發(fā)階段為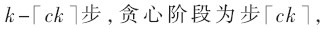 當(dāng)c=1時(shí)表明此時(shí)為純KK貪心算法。實(shí)驗(yàn)使用的數(shù)據(jù)集來(lái)自公開(kāi)數(shù)據(jù)[8],社區(qū)密度是每個(gè)社區(qū)平均所含節(jié)點(diǎn)數(shù)。數(shù)據(jù)集統(tǒng)計(jì)信息如表2所示。
當(dāng)c=1時(shí)表明此時(shí)為純KK貪心算法。實(shí)驗(yàn)使用的數(shù)據(jù)集來(lái)自公開(kāi)數(shù)據(jù)[8],社區(qū)密度是每個(gè)社區(qū)平均所含節(jié)點(diǎn)數(shù)。數(shù)據(jù)集統(tǒng)計(jì)信息如表2所示。

第一個(gè)數(shù)據(jù)集是計(jì)算機(jī)類英文文獻(xiàn)數(shù)據(jù)中的論文作者合作網(wǎng)絡(luò),邊代表兩個(gè)作者共同發(fā)表過(guò)論文,邊上的權(quán)重值表示作者間的合作次數(shù)。第二個(gè)數(shù)據(jù)集是視頻分享網(wǎng)站Youtube中的用戶視頻分享網(wǎng),邊代表用戶間為彼此分享過(guò)視頻,邊上的權(quán)重值代表用戶共享視頻的次數(shù)。第三個(gè)數(shù)據(jù)集是Google公司推出的免費(fèi)在線社交網(wǎng)站Orkut的朋友關(guān)系網(wǎng),邊代表用戶間是朋友關(guān)系,邊上權(quán)重值表示用戶交流次數(shù)。
為了充分說(shuō)明本文提出的基于社區(qū)度影響力最大化算法,實(shí)驗(yàn)在3個(gè)數(shù)據(jù)集上,從不同k值下的影響范圍和算法運(yùn)行時(shí)間兩方面將本文提出的CDEA算法與KK算法、HPG算法進(jìn)行對(duì)比,驗(yàn)證算法在大規(guī)模社會(huì)網(wǎng)絡(luò)下的準(zhǔn)確性和高效性。
2.1 影響范圍對(duì)比
首先考察Youtube數(shù)據(jù)集中CDEA算法在不同啟發(fā)因子c下影響范圍的變化,實(shí)驗(yàn)結(jié)果如圖1所示。由圖可知,除c=0外,其他c值影響范圍基本都比c=1大,且c=0.5時(shí)影響范圍最大。由于c=1時(shí),CDEA算法只有貪心階段沒(méi)有啟發(fā)階段,因此影響范圍比其他c值的影響范圍小。c=0表明此時(shí)CDEA算法只有啟發(fā)階段沒(méi)有貪心階段,所有初始節(jié)點(diǎn)都是靜態(tài)選擇PI最大的節(jié)點(diǎn),沒(méi)有傳播過(guò)程參與,因此影響范圍最小。實(shí)驗(yàn)結(jié)果表明c=0.5時(shí)CDEA算法影響范圍最大,因此下面的實(shí)驗(yàn)中設(shè)c=0.5。

其次考察3個(gè)數(shù)據(jù)集上CDEA算法影響范圍的變化,實(shí)驗(yàn)結(jié)果如圖2所示。由圖可知相同k值下,Youtube數(shù)據(jù)集上CDEA算法的影響范圍最大,Orkut數(shù)據(jù)集中影響范圍最小,這說(shuō)明本文提出的算法更適用于社區(qū)密度比較大的社會(huì)網(wǎng)絡(luò)。隨著初始種子節(jié)點(diǎn)k逐漸變大,CDEA算法在3個(gè)數(shù)據(jù)集上影響范圍隨之?dāng)U大,且當(dāng)k在[80,160]之間時(shí)影響范圍的變化速率比較大,k值超過(guò)160后影響范圍變化速率逐漸減小,這是因?yàn)殡S著k的增大,新增加的種子節(jié)點(diǎn)能激活的節(jié)點(diǎn)不斷減少,其影響范圍也在降低。

最后考察Youtube數(shù)據(jù)集中KK算法、HPG算法、CDEA算法在不同k值下影響范圍的變化,實(shí)驗(yàn)結(jié)果如圖3所示。由圖可知,KK算法的影響范圍呈線性,HPG和CDEA算法呈曲線上升,且CDEA算法在k值大于120時(shí)比HPG算法影響范圍大,這是因?yàn)镃DEA算法綜合考慮了節(jié)點(diǎn)度、社區(qū)度以及社區(qū)規(guī)模均值3個(gè)因素,使影響傳播的范圍在大規(guī)模社會(huì)網(wǎng)絡(luò)中更廣。

2.2 運(yùn)行時(shí)間對(duì)比
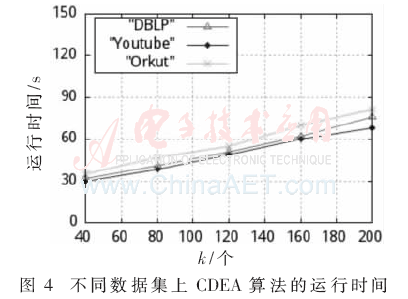
首先對(duì)比3個(gè)數(shù)據(jù)集上CDEA算法尋找k個(gè)種子節(jié)點(diǎn)需要的運(yùn)行時(shí)間,實(shí)驗(yàn)結(jié)果如圖4所示。由圖可知,算法在Youtube數(shù)據(jù)集上運(yùn)行時(shí)間最小,在Orkut數(shù)據(jù)集上運(yùn)行時(shí)間最大,這是由于CDEA算法充分利用了節(jié)點(diǎn)的社區(qū)度屬性,而Youtube數(shù)據(jù)集社區(qū)密度大,因此運(yùn)行時(shí)間相對(duì)比較小。當(dāng)k值不斷變大時(shí),CDEA算法在不同數(shù)據(jù)集中運(yùn)行時(shí)間的增長(zhǎng)率比較小,因?yàn)樵撍惴ǔ浞挚紤]了社會(huì)網(wǎng)絡(luò)中社區(qū)的邊界節(jié)點(diǎn),更適合大規(guī)模社會(huì)網(wǎng)絡(luò)。
最后在Youtube數(shù)據(jù)集中比較CDEA、HPG、KK算法的運(yùn)行時(shí)間。實(shí)驗(yàn)結(jié)果如圖5所示。由圖可知,隨著k值的不斷增長(zhǎng),KK算法的運(yùn)行時(shí)間不斷變長(zhǎng),而CDEA和HPG算法的運(yùn)行時(shí)間相對(duì)比較穩(wěn)定,呈線性增長(zhǎng),且當(dāng)k不斷變大時(shí),CDEA算法的運(yùn)行時(shí)間低于HPG算法。這是因?yàn)镃DEA算法充分考慮了社區(qū)邊界節(jié)點(diǎn),尤其是在大規(guī)模社會(huì)網(wǎng)絡(luò)中,極大地減少了尋找初始種子節(jié)點(diǎn)的時(shí)間。

3 總結(jié)
本文提出一種基于社區(qū)度的邊界節(jié)點(diǎn)影響力最大化算法CDEA,與其他關(guān)于影響力最大化問(wèn)題研究不同的是:CDEA算法利用社會(huì)網(wǎng)絡(luò)的社區(qū)結(jié)構(gòu),將社區(qū)中的邊界節(jié)點(diǎn)作為最有影響力節(jié)點(diǎn)的候選集,在兩層算法模型框架下,啟發(fā)階段根據(jù)網(wǎng)絡(luò)社區(qū)從邊界節(jié)點(diǎn)中選擇具有潛在影響力的節(jié)點(diǎn)集,貪心階段在啟發(fā)階段基礎(chǔ)上應(yīng)用KK算法計(jì)算。實(shí)驗(yàn)表明,本文提出的算法既有效地降低了時(shí)間復(fù)雜度,又能較好地應(yīng)用于大規(guī)模社會(huì)網(wǎng)絡(luò)。接下來(lái)的工作將對(duì)算法作進(jìn)一步改進(jìn),改善評(píng)估節(jié)點(diǎn)影響力的因素,提高算法的精度。
參考文獻(xiàn)
[1] LI G,CHEN S,F(xiàn)ENG J,et al.Efficient location-aware influence maximization[C].Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data.Snowbird,Utah,2014:1621.
[2] KIM J,KIM S K,YU H.Scalable and parallelizable prcessing of influence maximization for large-scale social networks[C].Proceedings of the 29th IEEE International Conference on Data Engineering.Brisbane,Australia,2013:266-277.
[3] 趙之瀅,于海,朱志良,等.基于網(wǎng)絡(luò)社團(tuán)結(jié)構(gòu)的節(jié)點(diǎn)傳播影響力分析[J].計(jì)算機(jī)學(xué)報(bào),2014,37(4):753-766.
[4] JUNG K,HEO W,CHEN W.IRIE:Scalable and robust influence maximization in social networks[C].Proceedings of the 12th International Conference on Data Mining.Brussels,Belgium,2012:918-923.
[5] GUO J,ZHANG P,ZHOU C,et al.Personalized influence maximization on social networks[C].Proceedings of the 22nd ACM International Conference on Information & Knowledge Management.San Francisco,USA,2013:199-208.
[6] CAO T,WU X,WANG S,et al.OASNET:an optimal allocation approach to influence maximization in modular social networks[C].Proceedings of the 2010 ACM Symposium on Applied Computing.ACM,2010:1088-1094.
[7] 田家堂,王軼彤,馮小軍.一種新型的社會(huì)網(wǎng)絡(luò)影響力最大化算法[J].計(jì)算機(jī)學(xué)報(bào),2011,34(10):1956-1965.
[8] YANG J,LESKOVEC J.Defining and evaluating network communities based on ground-truth[C].Proceedings of the ACM SIGKDD Workshop on Mining Data Semantics.ACM,2012:3.

