摘  要： 針對基本果蠅優(yōu)化算法（FOA）收斂速度慢和尋優(yōu)精度不高的缺點(diǎn),，在位置更新公式中引入加權(quán)因子,，提出了基于線性遞減策略和先增后減策略的兩種加權(quán)果蠅優(yōu)化算法（WFOA），從而增強(qiáng)了種群的多樣性,。通過對6個(gè)測試函數(shù)的仿真實(shí)驗(yàn),，驗(yàn)證了這些策略的可行性，表明這些策略能夠有效地提高算法的收斂速度和搜優(yōu)精度,。經(jīng)過兩種策略的對比,，發(fā)現(xiàn)線性遞減策略具有更快的收斂速度，而先增后減策略具有更強(qiáng)的魯棒性和稍好的尋優(yōu)精度,。

　　關(guān)鍵詞： 加權(quán)因子,；果蠅優(yōu)化算法；線性遞減策略,；先增后減策略

　　果蠅優(yōu)化算法FOA（Fruit Fly Optimization Algorithm）是由臺灣博士潘文超于2011年提出的,，與蟻群算法和粒子群算法類似，是基于動(dòng)物群體覓食行為演化出的一種尋求全局優(yōu)化的新方法[1-3],。它不同于順序執(zhí)行的傳統(tǒng)智能算法,，而是以果蠅群體自組織性和并行性為基礎(chǔ)，構(gòu)造出的一種動(dòng)物自治體模型,。FOA有著算法簡單,、控制參數(shù)少、容易實(shí)現(xiàn),、且具有一定并行性等特點(diǎn),，因此在各領(lǐng)域得到廣泛應(yīng)用[4]。FOA可以優(yōu)化神經(jīng)網(wǎng)絡(luò)參數(shù),，已成功應(yīng)用于企業(yè)經(jīng)營績效評估,、外貿(mào)出口預(yù)測、原油含水率預(yù)測等[3,，5-6],；FOA也可優(yōu)化支持向量機(jī)模型，已成功應(yīng)用于故障診斷,、物流需求量預(yù)測等[7-8],。但由于FOA是較晚提出的一種隨機(jī)搜索算法，其在理論分析和應(yīng)用研究等方面還處于初級階段,，同時(shí)也存在易發(fā)散,、收斂精度不高等缺點(diǎn)。

　　本文針對FOA收斂速度慢,、收斂精度低等缺點(diǎn),，提出了加權(quán)果蠅優(yōu)化算法WFOA（Weighted Fruit Fly Optimization Algorithm），進(jìn)而對幾種不同加權(quán)策略下的果蠅優(yōu)化算法進(jìn)行了對比研究。

1 果蠅優(yōu)化算法及其改進(jìn)

　　1.1 果蠅優(yōu)化算法

　　FOA在計(jì)算方法上類似于遺傳算法,，但不同的是FOA不使用雜交和變異等算子,，而是通過模仿果蠅特殊的嗅覺和視覺特點(diǎn)來進(jìn)行搜索。果蠅的嗅覺器官能很好地搜集飄浮在空氣中的各種氣味,，甚至能嗅到幾十公里以外的食物源,。然后飛近食物位置，使用敏銳的視覺發(fā)現(xiàn)食物與同伴聚集的位置,，并且往該方向飛去[2]。

　　根據(jù)果蠅搜索食物的特性,，將果蠅優(yōu)化算法歸納為以下幾個(gè)必要的步驟[1-3]：

　?。?）給定群體規(guī)模Sizepop，最大迭代次數(shù)Maxgen,，隨機(jī)初始化果蠅群體位置X_axis,，Y_axis；

　?。?）賦予果蠅個(gè)體利用嗅覺搜尋食物的方向與距離：

　　Xi=X_axis+Random ValueYi=Y_axis+Random Value（1）

　?。?）由于無法得知食物位置，因此先估計(jì)與原點(diǎn)的距離Disti,，再計(jì)算味道濃度判定值Si,，此值為距離的倒數(shù)：

　　Si=1/Disti（3）

　　（4）將味道濃度判定值代入味道濃度判定函數(shù)（或稱為適應(yīng)度函數(shù)Fitness Function）,，以求出果蠅個(gè)體的味道濃度Smelli：

　　Smelli=Function（Si）（4）

　?。?）找出該果蠅群體中味道濃度最佳的果蠅（求極小值）：

　　[bestSmell bestindex]=min（Smelli）（5）

　　（6）記錄并保留最佳味道濃度值bestSmell與其X,、Y坐標(biāo),，此時(shí)果蠅群體利用視覺向該位置（Fly2）飛去，形成新的群聚位置：

　　Smellbest=bestSmellX_axis=X（bestindex）Y_axis=Y（bestindex）（6）

　?。?）進(jìn)入迭代尋優(yōu),，重復(fù)執(zhí)行步驟（2）~步驟（5），并判斷最佳味道濃度是否優(yōu)于前一迭代最佳味道濃度,，前提是當(dāng)前迭代次數(shù)小于等于Maxgen,，若是則執(zhí)行步驟（6）。

　　1.2 加權(quán)果蠅優(yōu)化算法（WFOA）

　　在FOA中,，每個(gè)果蠅個(gè)體在n維搜索空間中通過適應(yīng)度函數(shù)來衡量個(gè)體的優(yōu)劣,，當(dāng)種群完成一次迭代后，與群體的歷史最佳位置比較得出新的最佳位置,，進(jìn)而在新最佳位置附近繼續(xù)隨機(jī)尋優(yōu),。由式（1）可以看出，迭代搜索始終在以當(dāng)前最優(yōu)位置為中心，以隨機(jī)飛行方向與距離Random Value為半徑的領(lǐng)域內(nèi)展開,，果蠅群體被限定在過分狹小的搜索范圍內(nèi),，降低了種群的多樣性[9]。受PSO（粒子群算法）的慣性權(quán)重啟發(fā)[10-11],，在迭代位置更新公式中引入加權(quán)因子w,，將式（1）變更如下，其他步驟不變,。

　　Xi=w×X_axis+Random ValueYi=w×Y_axis+Random Value（7）

　　在迭代尋優(yōu)過程中,，希望前期具有較強(qiáng)的“探索”能力，即較強(qiáng)的全局搜索能力,，以得到合適的種子,，而在迭代后期，應(yīng)具有較強(qiáng)的“開發(fā)”能力,，即較強(qiáng)的局部搜索能力,，從而展開精細(xì)的局部搜索。前期具有較大的值,，一方面是對自己“歷史經(jīng)驗(yàn)”的認(rèn)可,，能夠充分利用果蠅個(gè)體本身的歷史記憶；另一方面使得個(gè)體搜索的區(qū)域范圍變大,，讓果蠅個(gè)體在更廣的可行域里進(jìn)行搜索,，整個(gè)群體找到最優(yōu)解的概率就大，相應(yīng)的全局搜索能力就強(qiáng),。隨著迭代進(jìn)行到后期,，需要較小的w值，使其可搜索的范圍相對縮小,，這時(shí)主要根據(jù)隨機(jī)飛行方向與距離Random Value,，在“以往經(jīng)驗(yàn)”尋到的最優(yōu)解附近進(jìn)行小范圍精細(xì)搜索。

　　1.3 加權(quán)因子的幾種調(diào)整策略

　　策略1 線性遞減

　　w1=Wmax-（Wmax-Wmin）/Maxgen×g（8）

　　策略2 先增后減

　　令d=g/Maxgen,，則有：

　　w2=d+1,，        0≤d≤0.4w2=-7/6×d+28/15，0.4≤d≤1（9）

　　其中,，g為當(dāng)前迭代數(shù),，Maxgen為最大迭代數(shù)，Wmax為最大加權(quán)因子,，Wmin為最小加權(quán)因子,。對于策略1，經(jīng)過實(shí)驗(yàn)仿真,，分別確定Wmax,、Wmin為1.4、0.7的最佳權(quán)值范圍，隨著迭代數(shù)的變化,，權(quán)值從1.4線性遞減到0.7,，具體參數(shù)設(shè)置見式（8）。對于策略2,，從第一次迭代開始到第Maxgen的40%代,，權(quán)值從1線性遞增到1.4，而從Maxgen的40%代直至迭代結(jié)束,，權(quán)值從1.4線性遞減到0.7,，具體參數(shù)設(shè)置見式（9），兩種策略隨迭代的權(quán)值變化如圖1所示,。

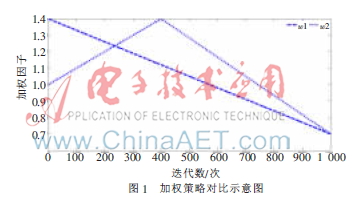
　　由式（8）和圖1可看出,，策略1在進(jìn)化初期具有很強(qiáng)的全局搜索能力。如果在初期能搜索到最好點(diǎn),，可在迭代前期達(dá)到快速收斂,。由式（9）和圖1可看出,，策略2在迭代開始至Maxgen的40%期間,，全局搜索能力逐漸增強(qiáng)，而從Maxgen的40%到結(jié)束期間,，其全局搜索能力逐漸減弱,。由此可知，在沒有陷入局部極值的情況下,，策略1比策略2應(yīng)該具有更快的收斂速度,。

2 實(shí)驗(yàn)仿真及結(jié)果分析

　　2.1 實(shí)驗(yàn)設(shè)計(jì)

　　為了測試w0-FOA、w1-FOA,、w2-FOA算法的尋優(yōu)性能,，本文選用6個(gè)常用于優(yōu)化算法比較的基準(zhǔn)函數(shù)，函數(shù)形式,、搜索區(qū)間,、理論極值和目標(biāo)精度如表1所示[4]。其中w0-FOA是w取固定值1,，即基本FOA算法,。具體參數(shù)設(shè)置為：群體規(guī)模Sizepop=30，最大迭代數(shù)Maxgen=1 000,；隨機(jī)初始化果蠅群體位置為表1中各函數(shù)的搜索區(qū)間,；迭代的果蠅搜尋食物的隨機(jī)飛行方向與距離區(qū)間為[-1，1],。測試軟件平臺為Windows7,、MATLAB 2012b，機(jī)器主頻為2.5 GHz，內(nèi)存為2 GB,。

　　2.2 實(shí)驗(yàn)結(jié)果與分析

　　6個(gè)測試函數(shù)在固定迭代數(shù)為1 000次,，分別采用w0-FOA、w1-FOA和w2-FOA經(jīng)過20次獨(dú)立運(yùn)行后的標(biāo)準(zhǔn)差,、優(yōu)化均值和最好解如表2~表7所示,；6個(gè)測試函數(shù)在表1中指定的目標(biāo)精度下經(jīng)過20次獨(dú)立運(yùn)行后的平均迭代次數(shù)和達(dá)優(yōu)率亦見表2~表7。其中,，平均迭代數(shù)是達(dá)到目標(biāo)精度的迭代數(shù)平均值,，達(dá)優(yōu)率為達(dá)到目標(biāo)精度的運(yùn)行次數(shù)與總實(shí)驗(yàn)次數(shù)之比。圖2是6個(gè)測試函數(shù)適應(yīng)度對數(shù)值進(jìn)化曲線（注：為了方便進(jìn)化曲線的顯示和觀察,，本文對函數(shù)的適應(yīng)度取以10為底的對數(shù)）,。

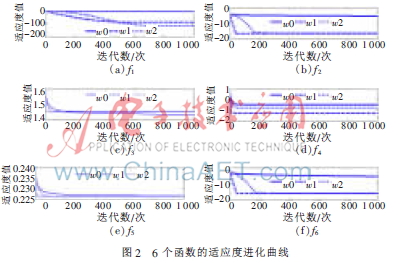
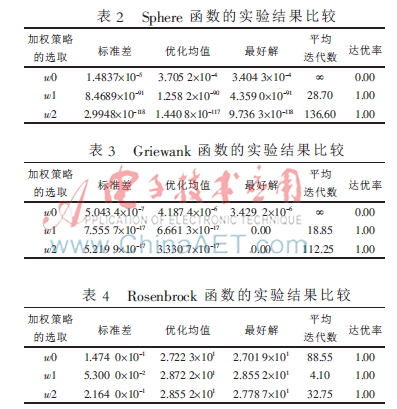
　　從表2、3,、7可以看出,，w0-FOA對f1、f2,、f6未能達(dá)到目標(biāo)精度,，而w1-FOA和w2-FOA都能100%達(dá)到目標(biāo)精度，并且改進(jìn)算法的收斂精度與w0-FOA的收斂精度相差11個(gè)數(shù)量級以上,。從表6可以看出,，雖然3種策略對f5均未達(dá)到指定的目標(biāo)精度，但是w1-FOA和w2-FOA找到的最好解要比w0-FOA找到的優(yōu),。而從表5可以看出,，w1-FOA的均值和魯棒性是其中最好的，w2-FOA和w0-FOA的優(yōu)化均值相差不大,，但是w2-FOA找到的最好解要比w0-FOA找到的最好解優(yōu)11個(gè)數(shù)量級,。其中效果不太好的是f3函數(shù)，因?yàn)榇撕瘮?shù)的全局最優(yōu)點(diǎn)隱藏在一條狹長的通道中,，對外提供很少的信息,，使算法很難辨別搜索方向，WFOA的優(yōu)勢體現(xiàn)不出,。

　　由圖2和表2~表7可看出,，w1-FOA最多只需28.70次迭代就能達(dá)到目標(biāo)精度（除f5），w2-FOA也最多只需136.60次迭代就可達(dá)到目標(biāo)精度（除f5）,，由此可見,，WFOA對收斂速度的影響非常顯著。

　　本文提出的WFOA算法在引入加權(quán)因子的基礎(chǔ)上,，對粒子群算法中的線性遞減策略和先增后減策略公式進(jìn)行了適當(dāng)?shù)膮?shù)調(diào)整,，經(jīng)測試函數(shù)驗(yàn)證發(fā)現(xiàn),，總體上改進(jìn)算法比原算法具有更快的收斂速度和更好的收斂精度，但w1-FOA比w2-FOA具有更快的收斂速度,，而w2-FOA具有更強(qiáng)的魯棒性和稍好的尋優(yōu)精度,。值得注意的是，不同加權(quán)策略對收斂速度的影響非常明顯,，如何正確選擇權(quán)值策略和適當(dāng)參數(shù),，使收斂速度和收斂精度達(dá)到最佳平衡，是接下來需要研究的問題,。

　　參考文獻(xiàn)

　　[1] PAN W T. A new fruit fly optimization algorithm： taking the financial distress model as an example[J]. Knowledge-based Systems,， 2012，26：69-74.

　　[2] 潘文超.果蠅最佳化演算法[M].臺北：滄海書局,，2011.

　　[3] 潘文超.應(yīng)用果蠅優(yōu)化算法優(yōu)化廣義回歸神經(jīng)網(wǎng)絡(luò)進(jìn)行企業(yè)經(jīng)營績效評估[J].太原理工大學(xué)學(xué)報(bào)（社會科學(xué)版）,，2011，29（4）：1-5.

　　[4] 韓俊英,，劉成忠.基于細(xì)菌趨化的果蠅優(yōu)化算法[J].計(jì)算機(jī)應(yīng)用,，2013，33（4）：964-966.

　　[5] 許智慧,，王福林,，孫丹丹，等.基于FOA_RBF神經(jīng)網(wǎng)絡(luò)的外貿(mào)出口預(yù)測[J].數(shù)學(xué)的實(shí)踐與認(rèn)識,，2012,，42（13）：14-19.

　　[6] 劉翠玲,，張路路,，王進(jìn)旗，等.基于FOA—GRNN油井計(jì)量原油含水率的預(yù)測[J].計(jì)算機(jī)仿真,，2012,，29（11）：243-246.

　　[7] 張翔，陳林.基于果蠅優(yōu)化算法的支持向量機(jī)故障診斷[J].電子設(shè)計(jì)工程,，2013,，21（16）：90-93.

　　[8] 李泓澤，郭森,，李春杰.果蠅優(yōu)化最小二乘支持向量機(jī)混合預(yù)測模型[J].經(jīng)濟(jì)數(shù)學(xué),，2012，29（3）：103-106.

　　[9] 潘峰,，李位星,，高琪，等.粒子群優(yōu)化算法與多目標(biāo)優(yōu)化[M].北京：北京理工大學(xué)出版社,，2013.

　　[10] SHI Y,， EBERHART R. Empirical study of particle swarm optimization[C]. International Conference on Evolutionary,，Washington： USA，1999：1945-1950.

　　[11] 崔紅梅,，朱慶保.微粒群算法的參數(shù)選擇及收斂性分析[J].計(jì)算機(jī)工程與應(yīng)用,，2007，43（23）：89-91.