摘  要： 為了解決高階次,、多變量、非線性,、強耦合的直線二級倒立擺的穩(wěn)定控制問題,，設(shè)計了一種參數(shù)自校正模糊PI控制器算法,。結(jié)合線性二次型最優(yōu)調(diào)節(jié)器(LQR)方法,，設(shè)計了融合函數(shù)，降低了模糊控制器的維數(shù),、減少了控制器規(guī)則數(shù),、實現(xiàn)了參數(shù)在線自校正，進而提高了控制器的性能,。借助固高科技倒立擺硬件平臺,，采用MATLAB仿真及實時控制，系統(tǒng)均能在較短時間內(nèi)達到穩(wěn)定,，且控制效果較好,，滿足了穩(wěn)定性和魯棒性要求,。

　　關(guān)鍵詞： 二級倒立擺；參數(shù)自校正,；模糊控制,；融合函數(shù)；LQR

　　倒立擺系統(tǒng)廣泛地應(yīng)用在非線性控制理論和研究方面,。對于不同的倒立擺類型,，控制方法比較多，主要有：雙PID及自適應(yīng)PID控制[1],、LQR及自適應(yīng)LQR[2],、LQG控制[3]、模糊邏輯控制[5-6],、自適應(yīng)滑模模糊控制[7],、模糊聚類[8]、神經(jīng)控制[9],、遺傳算法[10]等,，這些方法均能有效地控制倒立擺系統(tǒng)。但這些控制算法有其優(yōu)缺點,，同樣復(fù)雜的控制算法,，實時控制效果不是很好，增加了實現(xiàn)的難度,。PID控制器能夠有效地處理穩(wěn)定狀態(tài)響應(yīng),，但是，要想精確地調(diào)整PID控制器的增益是相當(dāng)困難的,；LQR算法在線性系統(tǒng)中能夠較好運用,，而在非線性較強的系統(tǒng)中也存在一些不足之處；參考文獻[5-8]在模糊邏輯控制的基礎(chǔ)上采用不同的算法,，能夠有效地控制非線性系統(tǒng),。模型建立好之后，非線性系統(tǒng)總是線性化在平衡點附近,。忽略其他次要部分,，這也會導(dǎo)致大的誤差；遺傳算法控制能夠在全局范圍內(nèi)進行優(yōu)化,，具有更高的效率,，但是也存在不足之處。其交叉和突變作用,，不能夠確保個體具有較好的適應(yīng)度,，給目標(biāo)函數(shù)的選取增加了困難。

　　本文在總結(jié)模糊控制和LQR算法基礎(chǔ)上,，設(shè)計了一種參數(shù)自校正模糊PI控制器,。運用LQR方法,，設(shè)計了融合函數(shù)，對模糊控制器進行降階處理,，實現(xiàn)參數(shù)在線自校正,。通過仿真實驗結(jié)果顯示，這種模糊控制方法能有效控制二級倒立擺系統(tǒng),。

　　1 二級倒立擺物理模型

　　在忽略空氣阻力,、各種接觸摩擦之后，將二級倒立擺系統(tǒng)等效為小車,，勻質(zhì)桿和質(zhì)量塊組成的剛性系統(tǒng)如圖1所示,，物理參數(shù)如表1所示。

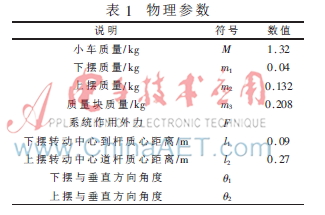
　　通過調(diào)用MATLAB函數(shù)可以判斷,，二級倒立擺系統(tǒng)是能控能觀的,。由于開環(huán)極點為p1，2,，3,，4=0、p5,，6=±6.2074j,，可知系統(tǒng)是不穩(wěn)定的。要使系統(tǒng)穩(wěn)定,，就需要外加控制器,。

　　2 參數(shù)自校正模糊PI控制器的設(shè)計

　　2.1 融合函數(shù)的設(shè)計

　　二級倒立擺系統(tǒng)有小車位移和速度、下擺角度和角速度,、上擺角度和角速度6個變量,，如果將這6個變量作為模糊控制器的輸入，每個輸入變量在論域范圍內(nèi)取7個模糊子集,，則會出現(xiàn)76=117 649條推理規(guī)則,，這會大大影響模糊控制器的性能。由于線性系統(tǒng)具有可融合的特點,，在此將二級倒立擺系統(tǒng)6個變量融合成為綜合誤差E和綜合誤差變化量EC,，作為模糊控制器的輸入，則融合函數(shù)設(shè)計如下[12],。

　　(1)利用現(xiàn)代控制中的LQR方法,，通過仿真試湊法選取使二級倒立擺系統(tǒng)的二次型性能指標(biāo)J=[XTQX+UTRU]dt為最小值的Q、R(Q,、R為適當(dāng)維數(shù)的正定加權(quán)矩陣)，從而可以計算得出狀態(tài)反饋矩陣：

　　2.2 參數(shù)自校正模糊PI控制器的設(shè)計

　　在基本模糊控制器基礎(chǔ)上,，設(shè)計了參數(shù)自校正模糊PI控制器[5-8],。經(jīng)上述融合函數(shù)降維后,，根據(jù)圖2所示的模糊控制二級倒立擺結(jié)構(gòu)圖，選擇合適的量化因子Ke,、Kec和比例因子Ku,。E、EC作為模糊控制器1的輸入量,，U作為輸出控制量,。輸入量和輸出量均采用三角型隸屬度函數(shù)進行模糊化，每個語言變量的論域為{-6,，6},，語言值設(shè)為{PB，PM,，PS,，ZE，NS,，NM,，NB}，分別表示{正大,，正中,，正小，零,，負小,，負中，負大},，以重心法解模糊化[13],。模糊控制器1控制規(guī)則表如表2所示。

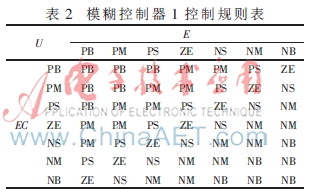
　　為了對模糊控制器1的參數(shù)Ke,、Kec,、Ku進行自校正，引入模糊控制器2,，其調(diào)整方法為：當(dāng)系統(tǒng)的誤差E和誤差的變化EC較大時,，應(yīng)加快系統(tǒng)響應(yīng)速度，此時需要降低量化因子Ke和Kec來降低E和EC輸入量的分辨率,，同時加大比例因子Ku,，使響應(yīng)加快；當(dāng)E和EC較小時,，說明系統(tǒng)已經(jīng)趨于穩(wěn)定,，此時要求提高系統(tǒng)精度，要增大量化因子Ke和Kec來提高對輸入變化的分辨率,，同時減小比例因子,，以減小超調(diào)量,。此處Ke、Kec增加的倍數(shù)與比例因子Ku的減小倍數(shù)相同,。

　　選擇輸入量和輸出量均為三角型隸屬度函數(shù)進行模糊化,，取Ke、Kec的論域為{-6,，6},，在論域范圍內(nèi)把E、EC劃分為{NB,，NS,，NM，ZE,，PS,，PM，PB}7個模糊子集,，取定義Ku的論域為{0.125,，0.25，0.5,，1,，2，4,，8},，模糊子集定義為{AH，AM,，AL,，KO，CL,，CM,，CH},，分別表示{高放,，中放,，低放,，不變，低縮,，中縮,，高縮},，以重心法解模糊化,。模糊控制器2控制規(guī)則表如表3所示,。

　　其中，參數(shù)調(diào)整方法為：(1)以原始的Ke、Kec對E,、EC進行量化得到E′,、EC′,；(2)將E′,、EC′作為模糊控制器2的輸入量，輸出控制量為調(diào)整倍數(shù)M

　　對整定得出的控制量u與系統(tǒng)輸入量作差,，作為PI控制器的輸入,，再將PI控制器的輸出作為二級倒立擺狀態(tài)模型的輸入，即可以對二級倒立擺系統(tǒng)進行仿真研究,。

　　3 仿真結(jié)果分析

　　在Simulink環(huán)境中建立的二級倒立擺的參數(shù)自校正模糊PI和模糊控制器的仿真結(jié)構(gòu)圖如圖3所示,。

　　根據(jù)式(1)，取Q=diag(1000,，500,，500，0,，0,，0)，R=1,，采用LQR方法得到狀態(tài)反饋矩陣K為：

　　K=[31.622 8  113.123 5  -227.437 8

　　28.301 8  1.071 5  -38.755 3]

　　代入式(3),，得融合函數(shù)為：

　　取系統(tǒng)的初始值為零，設(shè)置仿真時間為5 s,，仿真步長為5 ms,，通過多次調(diào)整參數(shù)，得到兩種控制器仿真曲線圖如圖4所示,。由圖4可知,，小車最終距離初始位置10 cm左右處保持平衡，下擺擺角偏離平衡位置最大值為0.05 rad,，上擺擺角偏離平衡位置最大值為0.003 rad,，系統(tǒng)能在2.5 s左右時間內(nèi)達到并維持平衡，由此可見控制效果比較理想,。比較兩者的仿真結(jié)果可知,，基于融合函數(shù)的參數(shù)自校正模糊PI控制器不僅能使小車維持平衡，而且系統(tǒng)的響應(yīng)速度也較快,，可以用來對二級倒立擺實物系統(tǒng)實時控制,。

　　在基本模糊控制器結(jié)構(gòu)上，設(shè)計了一種參數(shù)自校正模糊PI控制器,，通過融合函數(shù)對模糊控制器的輸入進行降維,，避免了控制規(guī)則過多而影響控制性能的缺點，同時又對模糊控制器的量化因子和比例因子進行在線校正調(diào)整，達到了自校正目的,。為了測試倒立擺系統(tǒng)魯棒性,，選用了外部測試方法(即施加外力與系統(tǒng))，系統(tǒng)能夠很快校正偏差,，回到平衡位置,。仿真結(jié)果和圖5實時控制曲線表明，這種控制器能有效地控制二級倒立擺系統(tǒng),，具有良好的穩(wěn)態(tài)性能,，響應(yīng)速度較快，魯棒性較好,。

　　參考文獻

　　[1] GEORGE J,，KRISHNA B，GEORGE V I,，et al.Design of adaptive pid controller based on maximum modulus theoremfor inverted pendutum on a cart[J].Sensors & Transducers,，2012，145(10)：163-171.

　　[2] Zhang Jiaolong,，Zhang Wei.LQR self-adjusting based controlfor the planar double inverted pendulum[J].Physics Procedia,，2012(24)：1669-1676.

　　[3] EIDE R，EGELID P M,，STAMSO A,，et al.LQG control for balancing an inverted pendulum mobile robot[J].Intelligent Control and Automation，2011,，2(2)：160-166.

　　[4] Yi Jianqiang,，YUBAZAKI N，HIROTA K.A new fuzzy controller for stabilization of parallel-type double inverted pendulum system[J].Fuzzy Sets and Systems,，2002,，126(1)：105-119.

　　[5] KIZIR S，BINGUL Z,，OYSU C.Fuzzy control of a real timeinverted pendulum system[J].Journal of Intelligent & Fuzzy Systems,，2010(21)：123-133.

　　[6] Huang Chenghao，Wang Wenjuan,，Chiu Chihhui.Design andimplementation of fuzzy control on a two-wheel inverted pendulum[J].IEEE Transaction on Industrial Electronics,，2011，58(7)：2988-3001.

　　[7] Duan Xuechao,，Qiu Yuanying,，Duan Baoyan.Adaptive slidingmode fuzzy control of planar inverted pendulum[J].Control and Decision，2007,，22(7)：774-777.

　　[8] SIVARAMAN E,，ARULSELVI S.Modeling of an inverted pendulum based on fuzzy clustering techniques[J].Expert Systems with Applications,，2011，38(11)：13942-13949.

　　[9] HASSANZADEH I,，MOBAYEN S.PSO-based controller design for rotary inverted pendulum system[J].Journal of Applied Science,，2008，8(16)：2907-2912.

　　[10] Ping Zhaowu,，Huang Jie.Approximate output of spherical inverted pendulum by neural network control[J].Neurocomputing,，2012，85(5)：38-44.

　　[11] 宋君烈,，肖軍,，徐心和.倒立擺系統(tǒng)的Lagrange方程建模與模糊控制[J].東北大學(xué)學(xué)報(自然科學(xué)版),，2002,，23(4)：333-337.

　　[12] 邢景虎，陳其工,，江明.二級倒立擺基于融合函數(shù)的模糊控制[J].合肥工業(yè)大學(xué)學(xué)報(自然科學(xué)版),，2011，34(8)：1155-1158.

　　[13] 蔡自興.智能控制(第二版)[M].北京：電子工業(yè)出版社,，2004.