文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào): 0258-7998(2014)09-0098-03
中壓配電網(wǎng)載波通信是指利用10 kV配電網(wǎng)現(xiàn)有的物理網(wǎng)絡(luò)進(jìn)行數(shù)據(jù)通信和信息傳遞的技術(shù)。配電網(wǎng)在我國(guó)的建設(shè)已經(jīng)相當(dāng)完善,利用配電網(wǎng)實(shí)現(xiàn)通信,不需要重新布線,成本低廉,因此受到人們的廣泛關(guān)注[1]。該技術(shù)主要被應(yīng)用于中壓配電網(wǎng)的自動(dòng)化數(shù)據(jù)傳輸、電負(fù)荷控制、電網(wǎng)運(yùn)行監(jiān)測(cè)和集中抄表等領(lǐng)域。但中壓電力線信道的通信環(huán)境惡劣,尤其是噪聲干擾比其他通信信道嚴(yán)重。而在噪聲干擾中,隨機(jī)脈沖噪聲是影響電力線通信的主要因素,同時(shí)它也是分析與建模中最難的,目前建模方法研究較少。脈沖噪聲的隨機(jī)性主要體現(xiàn)在其脈沖寬度和脈沖間隔時(shí)間的不確定性,這兩個(gè)參數(shù)需要使用隨機(jī)變量模型來模擬實(shí)現(xiàn)。
本文在測(cè)量和分析中壓電力線信道噪聲的基礎(chǔ)上,通過隱馬爾科夫鏈建立了脈沖寬度和脈沖間隔時(shí)間的概率統(tǒng)計(jì)模型,并進(jìn)行了相應(yīng)的計(jì)算和仿真。得到隨機(jī)脈沖噪聲的各個(gè)參數(shù)后,仿真得到了符合統(tǒng)計(jì)模型的隨機(jī)脈沖噪聲,為中壓電力線通信的進(jìn)一步研究提供了理論支持。
1 中壓電力線信道噪聲分析
中壓電力線信道噪聲并不是簡(jiǎn)單的加性高斯白噪聲,主要分為人為和非人為噪聲。人為噪聲來自電器、機(jī)電和電力線本身;非人為噪聲由自然現(xiàn)象引起,如雷電。根據(jù)參考文獻(xiàn)[2],中壓電力線信道噪聲主要分為隨機(jī)脈沖噪聲、窄帶噪聲和背景噪聲3類。實(shí)測(cè)發(fā)現(xiàn)信道中同時(shí)存在影響較小的異步于工頻的周期脈沖噪聲和同步于工頻的周期脈沖噪聲。
1.1 有色背景噪聲[3]
有色背景噪聲具有相對(duì)低的功率譜密度,它主要由各種低功率的噪聲源產(chǎn)生。經(jīng)測(cè)量和研究發(fā)現(xiàn),背景噪聲來源主要是交直流兩用電機(jī)。
1.2 窄帶噪聲
窄帶噪聲多為正弦調(diào)幅信號(hào),主要由電力線的中短波廣播引起。
1.3 隨機(jī)脈沖噪聲
隨機(jī)脈沖噪聲主要是由電器的開關(guān)、恒溫設(shè)備的啟動(dòng)及一些其他的開關(guān)現(xiàn)象造成的,其到達(dá)時(shí)間是隨機(jī)的,噪聲功率譜密度有時(shí)會(huì)比背景噪聲高出50 dB。
1.4 異步于工頻的周期脈沖噪聲
異步于工頻的周期脈沖噪聲主要由電視機(jī)或電腦顯示器干擾所造成,噪聲波形為按指數(shù)規(guī)律衰減的正弦波的疊加。這里要考慮噪聲的周期性,它的重復(fù)頻率與電視機(jī)或電腦顯示器的掃描頻率同步。
1.5 同步于工頻的周期脈沖噪聲
同步于工頻的周期性脈沖噪聲由可控硅整流器件造成,脈沖持續(xù)時(shí)間很短,脈沖寬度由可控硅整流器的導(dǎo)通與關(guān)斷時(shí)間決定,其脈沖的重復(fù)頻率為工頻或工頻的整數(shù)倍。
2 脈沖噪聲分析及其建模
隨機(jī)脈沖噪聲通常是由高壓開關(guān)的操作、系統(tǒng)內(nèi)開關(guān)瞬時(shí)的開斷、較大的負(fù)荷變化等引起,主要表現(xiàn)為能量很大的脈沖干擾或脈沖干擾群,它以無(wú)規(guī)律的間隔時(shí)間出現(xiàn)在整個(gè)電網(wǎng)中,持續(xù)時(shí)間短,其噪聲功率譜密度有時(shí)會(huì)比背景噪聲高出50 dB。該噪聲具有很大的不可預(yù)測(cè)性,是電力線信道噪聲中最復(fù)雜的一種。
脈沖噪聲對(duì)通信數(shù)據(jù)的影響主要由脈沖的幅度、脈沖寬度和脈沖間隔時(shí)間決定,其波形形式為按指數(shù)規(guī)律衰減的正弦波的疊加[4-6],如式(1)所示。

其中各個(gè)參數(shù)含義如下:
A為脈沖幅度,通過測(cè)量用統(tǒng)計(jì)的方法可得到其變化范圍,并且隨脈沖寬度的增加而減小。
τ為時(shí)間常數(shù),與脈沖寬度相對(duì)應(yīng),可由脈沖寬度的1/5來近似得到。
f為衰減正弦波的頻率,與參考文獻(xiàn)[7]類似,該頻率在500 kHz~30 MHz范圍內(nèi),并且符合Weibull分布,可根據(jù)分布函數(shù)產(chǎn)生。
φ在0~2π區(qū)間內(nèi)隨機(jī)產(chǎn)生。
3 脈沖噪聲的仿真
隨機(jī)脈沖噪聲具有隨機(jī)性,因此需用隨機(jī)變量來描述,本文使用隱馬爾科夫鏈(Hidden Markov Chain)模型對(duì)脈沖寬度和脈沖間隔時(shí)間進(jìn)行仿真。
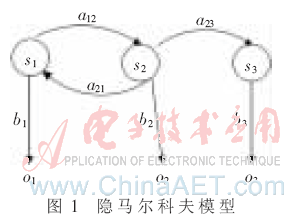
3.1 隱馬爾科夫模型簡(jiǎn)介
隱馬爾科夫模型是用來描述一個(gè)含有隱含未知參數(shù)的馬爾可夫過程。在該模型中,狀態(tài)不是直接可見的,但受狀態(tài)影響的某些變量則是可見的,每一個(gè)狀態(tài)在可能輸出的符號(hào)上都有一概率分布。
隱馬爾可夫模型定義為一個(gè)五元組<S,O,A,B,π>,其中
S={s1,s2,…,sN}:所有可能狀態(tài)所組成的集合。
O={o1,o2,…,oM}:觀察值的序列。
A為狀態(tài)轉(zhuǎn)移分布(也被稱為矩陣P),即S中各元素兩兩之間轉(zhuǎn)移的概率分布。
B為每種狀態(tài)輸出的概率分布。
π為初始狀態(tài)分布,用來確定系統(tǒng)的初始狀態(tài)。
圖1即為一個(gè)隱馬爾科夫模型的例子。
3.2 脈沖寬度和脈沖間隔時(shí)間的仿真
設(shè)系統(tǒng)有N個(gè)狀態(tài),那么矩陣P就是N×N的狀態(tài)轉(zhuǎn)移矩陣,矩陣B就是N×M的輸出概率矩陣。而對(duì)脈沖噪聲的脈寬和脈沖間隔來說,輸出狀態(tài)為有脈沖和無(wú)脈沖兩個(gè)狀態(tài),因此矩陣B就是N×2的輸出矩陣。
為了方便對(duì)脈沖寬度和脈沖間隔時(shí)間仿真,將系統(tǒng)N個(gè)狀態(tài)分為兩組A(1,2,…,w)和B(w+1,w+2,…,N),A中w個(gè)狀態(tài)表示有脈沖事件,B中N-w個(gè)狀態(tài)表示無(wú)脈沖事件。由于每組內(nèi)各狀態(tài)間不能相互轉(zhuǎn)移,因此仿真模型如圖2所示。
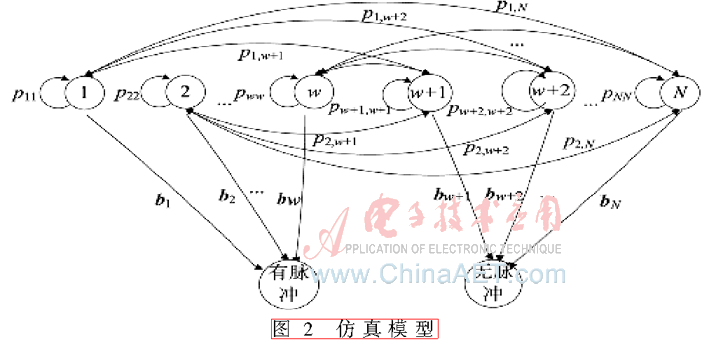
仿真模型中各個(gè)矩陣如下:
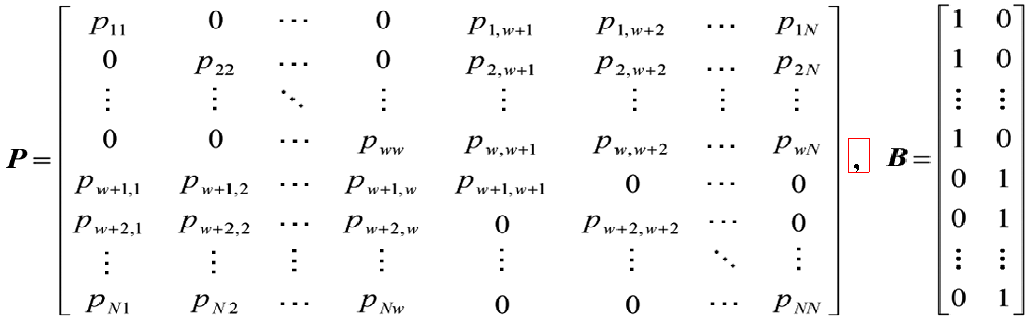
為了便于求解矩陣P中的未知數(shù),設(shè)從無(wú)脈沖狀態(tài)到狀態(tài)1,2,…,w的轉(zhuǎn)移概率為q1,q2,…,qw;設(shè)從有脈沖狀態(tài)到狀態(tài)w+1,w+2,…,N的轉(zhuǎn)移概率為qw+1,qw+2,…,qN。則有如下關(guān)系:
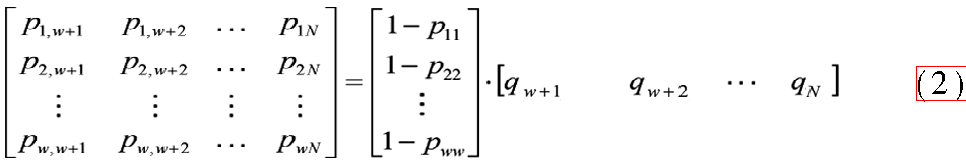
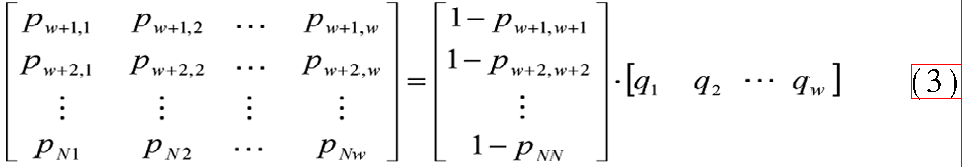
因此只要求出p11,p22,…,pNN和q1,q2,…,qN,便可以得到P矩陣中所有元素值。
定義累計(jì)概率函數(shù)為cpf(x),則有:cpf(x)=P(X>x)。
記cpfw為脈沖寬度大于某寬度的概率,使用離散時(shí)間應(yīng)表示為:
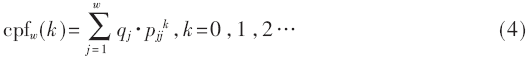
記cpft為脈沖間隔時(shí)間大于某時(shí)間值的概率,使用離散時(shí)間應(yīng)表示為:
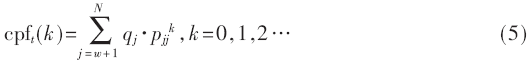
根據(jù)測(cè)量所得脈沖寬度和脈沖間隔時(shí)間的概率分布曲線圖,通過曲線擬合技術(shù)最終可確定矩陣P中所有元素值。
4 仿真結(jié)果
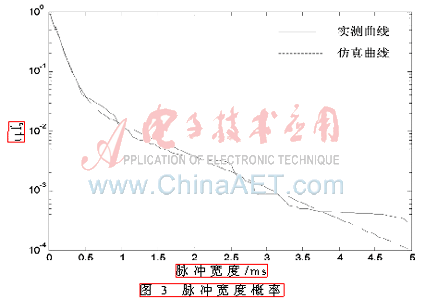
通過對(duì)脈沖寬度和脈沖間隔時(shí)間的連續(xù)測(cè)量與統(tǒng)計(jì),得到兩者的概率統(tǒng)計(jì)曲線如圖3和圖4中實(shí)線所示。
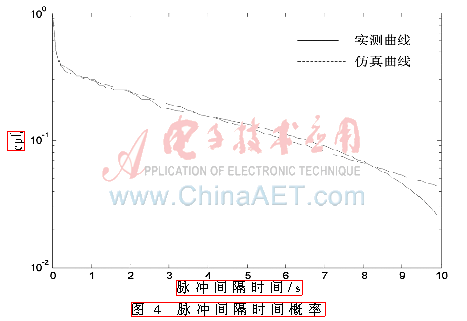
本文假設(shè)仿真模型中總狀態(tài)數(shù)為4,有脈沖和無(wú)脈沖狀態(tài)數(shù)各為2個(gè)(即w=2)。根據(jù)累計(jì)概率計(jì)算公式和統(tǒng)計(jì)概率曲線,通過曲線擬合技術(shù),得到模型的參數(shù)如下:

所得模型仿真曲線如圖3、圖4中虛線所示。由仿真結(jié)果可以看到,仿真曲線可以較好地模擬測(cè)量曲線。
由隱馬爾科夫模型得到脈沖寬度和脈沖間隔時(shí)間的概率分布函數(shù)后,即可產(chǎn)生符合各自概率分布函數(shù)的數(shù)據(jù)。最終將所得到的所有參數(shù)代入式(1)所示的隨機(jī)脈沖噪聲的波形表達(dá)式中,仿真得到的隨機(jī)脈沖噪聲如圖5所示。
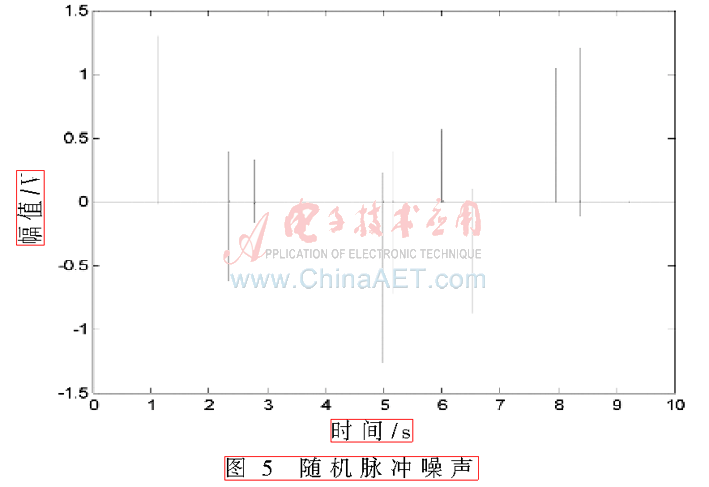
通過此脈沖噪聲的仿真圖像可以看出,脈沖噪聲參數(shù)基本符合所建模型。因此,所建立的隱馬爾科夫模型是可行的。
隨機(jī)脈沖噪聲干擾是影響電力線正常通信的最主要因素,由于其具有隨機(jī)性和時(shí)變性,它的突然出現(xiàn)會(huì)使電力線信道產(chǎn)生突發(fā)錯(cuò)誤。本文通過測(cè)量和分析中壓電力線信道噪聲,得到隨機(jī)脈沖噪聲的脈沖寬度和脈沖間隔時(shí)間的概率分布曲線;基于隱馬爾科夫鏈建立了統(tǒng)計(jì)模型,通過曲線擬合技術(shù)得到模型的參數(shù)值;最終仿真實(shí)現(xiàn)了符合統(tǒng)計(jì)特性的隨機(jī)脈沖噪聲,為中壓電力線通信的進(jìn)一步研究提供了理論基礎(chǔ)。
參考文獻(xiàn)
[1] 謝志遠(yuǎn),楊星,貢振崗,等.中壓配電網(wǎng)載波通信調(diào)制解調(diào)技術(shù)研究[J].電子技術(shù)應(yīng)用,2013,39(2):93-95.
[2] RAMSELER S,ARZBERGER M,HAUSER A.MV and LV powerline communications: new proposed IEC standards[C].Piscataway,NJ,USA:ABB Corp.Res.,Baden,Switzerland,1999.
[3] 邢志民,侯思祖.基于正交頻分復(fù)用的中壓帶寬電力線通信技術(shù)的研究與應(yīng)用[D].保定:華北電力大學(xué),2006.
[4] DEGARDIN V,LIENARD M,ZEDDAM A,et al.Classification and characterization of impulsive noise on indoor power line used for data communications[J].IEEE Transactions on Consumer Electronics,2002,48(4):913-918.
[5] CHAN M H L,DONALDSON R W.Amplitude,width and interarrival distributions for noise impulses on intrabuilding power line communication networks[J].IEEE Transactions on Electromagnetic Compatibility,1989,31(3):320-323.
[6] PANAYIOTIS G G,PANAGIOTIS T,CHRIS K.Alpha-stable modeling of noise and robust time-delay estimation in the presence of impulsive noise[J].IEEE Transactions on Multimedia,1999,1(3):291-301.
[7] 吳旭.低壓電力線載波通信噪聲環(huán)境的仿真研究[D].哈爾濱:哈爾濱理工大學(xué),2007.

