Kalman濾波理論在20世紀(jì)60年代一經(jīng)提出，便得到了軍事,、控制,、通信等領(lǐng)域的極廣泛的應(yīng)用,。它可以實(shí)現(xiàn)隨機(jī)干擾下的線性動(dòng)態(tài)系統(tǒng)的最優(yōu)估計(jì),，目前Kalman濾波器的實(shí)現(xiàn)方式主要有兩種，一是在PC機(jī)上實(shí)現(xiàn),，可以同時(shí)滿足計(jì)算精度和實(shí)時(shí)性的要求,，但是PC機(jī)體積大，質(zhì)量重,，成本高,；二是通過DSP等芯片來實(shí)現(xiàn)，用這種方式實(shí)現(xiàn)的Kalman濾波器雖然體積小,，質(zhì)量輕,，但是因其指令順序執(zhí)行的CPU架構(gòu)，在系統(tǒng)復(fù)雜時(shí)無法滿足系統(tǒng)的實(shí)時(shí)性要求,。隨著控制系統(tǒng)的復(fù)雜性的提高,，系統(tǒng)的階次變大，如組合導(dǎo)航系統(tǒng)的濾波,，其濾波的階次一般都要18階,，如果對系統(tǒng)進(jìn)一步細(xì)化建模或增加其復(fù)雜性,，其濾波階次可以達(dá)到幾十階,。因此,，Kalman濾波器在工程應(yīng)用中的實(shí)現(xiàn)遇到了系統(tǒng)體積、重量,、成本和系統(tǒng)精度,、速度等性能不能兼顧的問題。隨著現(xiàn)代電子技術(shù)的發(fā)展,，FPGA具有系統(tǒng)結(jié)構(gòu)和邏輯單元靈活,、集成度高以及適用范圍寬等特點(diǎn),，可以很好地解決這個(gè)難題,。因?yàn)镕PGA采用的是硬件并行算法，能很好的解決速度和實(shí)時(shí)性的問題,，并且其具有靈活的可配置特性和優(yōu)良的抗干擾能力,，使得FPGA構(gòu)成的數(shù)字信號處理系統(tǒng)非常易于修改、測試及硬件升級,。隨著FPGA技術(shù)的不斷成熟,，其內(nèi)嵌資源不斷豐富，硬核乘法器和塊RAM的數(shù)目不斷增長,，使得FPGA實(shí)現(xiàn)復(fù)雜的數(shù)字信號處理算法變得更為簡單和快速,。因此，本文對FPGA技術(shù)和Kalman濾波算法進(jìn)行結(jié)合研究,，探索Kalman濾波算法在FPGA中的實(shí)現(xiàn)方式并進(jìn)行性能驗(yàn)證,，以對基于FPGA的Kalman濾波算法的工程實(shí)現(xiàn)提供參考。

1 Kalman濾波算法理論

Kalman濾波是在時(shí)域內(nèi)以信號的一,、二階統(tǒng)計(jì)特性已知為前提,、以均方誤差極小為判據(jù)，能自動(dòng)跟蹤信號統(tǒng)計(jì)性質(zhì)的非平穩(wěn)變化,，具有遞歸性質(zhì)的一種算法,。它處理的對象是隨機(jī)系統(tǒng)，并能正確估計(jì)出有用信號,。設(shè)離散系統(tǒng)差分方程如下：



則Kalman濾波方程組如下：

狀態(tài)一步預(yù)測方程：



從式(1)～(6)可知,，若利用傳統(tǒng)的處理器實(shí)現(xiàn)Kalman濾波算法，由于其指令執(zhí)行的順序性,，至少需要分為5步來實(shí)現(xiàn),，其中每一步還都需要進(jìn)行至少1次的加法和乘法等運(yùn)算，每次運(yùn)算都要順序執(zhí)行,，其執(zhí)行速度和效率很低,；如果利用FPGA來進(jìn)行Kalman濾波，根據(jù)其各步的邏輯關(guān)系,，可以分為3步來實(shí)現(xiàn),，即第一步計(jì)算狀態(tài)一步預(yù)測值和一步預(yù)測均方誤差Pk+1／k,，第二步計(jì)算濾波增益Kk+1，第三步計(jì)算狀態(tài)最優(yōu)估值和估計(jì)均方誤差Pk+1／k+1,。由此可知,，利用FPGA技術(shù)可以實(shí)現(xiàn)Kalman濾波的并行計(jì)算，壓縮計(jì)算時(shí)間,，提高解算速度,。因此，對FPGA的Kalman濾波進(jìn)行研究開發(fā),，可實(shí)現(xiàn)基于FPGA的快速Kalman濾波解算,，滿足在對實(shí)時(shí)性要求更高的環(huán)境中使用。

2 在FPGA中實(shí)現(xiàn)Kalman濾波算法研究

由于FPGA實(shí)現(xiàn)Kalman濾波解算速度非?？?，若利用FPGA的串行口依次輸入觀測值，由于數(shù)據(jù)串行輸入的特點(diǎn),，會(huì)使FPGA的解算部分等待數(shù)據(jù)接收完畢才能執(zhí)行濾波解算,，導(dǎo)致整體的解算時(shí)間過長。為檢驗(yàn)FPGA實(shí)現(xiàn)Kalman濾波器的計(jì)算性能,，本文預(yù)先將觀測值輸入并保存于FPGA內(nèi)的ROM中,，以使FPGA可以連續(xù)地進(jìn)行濾波解算，實(shí)現(xiàn)方案原理如圖1所示,。



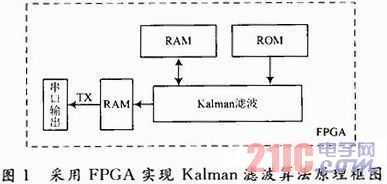
圖1中,，Kalman濾波解算在FPGA內(nèi)完成，RAM和ROM使用FPGA內(nèi)嵌的硬件RAM存儲器,，其中RAM暫存每步的中間結(jié)果,，ROM存放濾波中的固定系數(shù)，如觀測矩陣,、噪聲系數(shù)陣等,。Kalman濾波的解算過程主要利用內(nèi)嵌的硬核乘法器等資源來完成。因解算速度較快,，解算結(jié)果暫存于一個(gè)稍大的存儲器內(nèi),，同時(shí)通過串行口輸出到PC機(jī)上保存用于分析。該方案的關(guān)鍵問題是在FPGA中實(shí)現(xiàn)Kalman濾波算法,。

FPGA實(shí)現(xiàn)Kalman濾波器,，其實(shí)質(zhì)就是控制數(shù)據(jù)的轉(zhuǎn)移和存儲并實(shí)現(xiàn)矩陣的相乘、加,、減,、求逆等運(yùn)算。其中,，數(shù)據(jù)的轉(zhuǎn)移控制需要有限狀態(tài)機(jī)(FSM)來完成,，同時(shí)FPGA設(shè)計(jì)中,，不可避免的會(huì)遇到資源與速度的問題。因此,，需要對上述各關(guān)鍵技術(shù)進(jìn)行研究和實(shí)現(xiàn),。

2．1 矩陣相乘在FPGA中的實(shí)現(xiàn)

Kalman濾波計(jì)算中最基本的步驟就是矩陣相乘。對于其中最常見的D=A×B×C型的矩陣相乘,，有兩種實(shí)現(xiàn)方式：方式一,，分步相乘；方式二,，直接相乘,。事先將矩陣A，B,，C分別存入ROM1,，ROM2,，ROM3中,，方式一中，首先進(jìn)行兩個(gè)矩陣的相乘,，多路選擇開關(guān)MUX選通ROM1和ROM2,，依次讀取其中的數(shù)據(jù)進(jìn)行乘加，完成前面兩個(gè)矩陣的相乘,，結(jié)果存入ROMTEMP中,；然后，MUX選通ROMTEMP和ROM3,，利用前面同樣的資源,，完成三個(gè)矩陣的連乘。方式二中,，ROM1,，ROM2，ROM3同時(shí)輸出數(shù)據(jù),，MUX根據(jù)解算需要配置乘法器和加法器的輸入,，所有的過程同時(shí)進(jìn)行。從上面的執(zhí)行過程可知,，方式一的執(zhí)行需要占用更多的時(shí)間,，而方式二的執(zhí)行會(huì)占用更多的資源。對于上述N階的3個(gè)矩陣相乘,，其占用資源和所需時(shí)間如表1所示,。



由表1可知，對于維數(shù)越大的矩陣相乘,，需要的浮點(diǎn)加法器越多,。由于浮點(diǎn)加法器的生成利用FPGA內(nèi)的基本邏輯單元——可配置邏輯塊(CLB),，所以其占用的CLB等資源也越多。這種現(xiàn)象在上述方式二中尤為突出,。本文中研究擬先實(shí)現(xiàn)二階Kalman濾波器,，階次較低，資源相對充足,，為檢驗(yàn)FPGA實(shí)現(xiàn)Kalman濾波器的快速性,，選用第二種方式進(jìn)行矩陣相乘，以得到最快的解算速度,。

2．2 有限狀態(tài)機(jī)的運(yùn)用

有限狀態(tài)機(jī)是一種用來進(jìn)行對象行為建模的工具,，其作用主要是描述對象在它的生命周期內(nèi)所經(jīng)歷的狀態(tài)序列，以及如何響應(yīng)來自外界的各種事件,。Kalman濾波中,，由于解算過程中的邏輯關(guān)系，需要分步進(jìn)行,，所以需要用有限狀態(tài)機(jī)來控制各步的轉(zhuǎn)移,。根據(jù)各步間的邏輯關(guān)系，可以將其大致分為4個(gè)狀態(tài)：S0,，S1,，S2和S3狀態(tài)。其中,，S0為初始化狀態(tài),，之后進(jìn)入S1狀態(tài)，計(jì)算和Pk+1／k,，然后進(jìn)入S2狀態(tài),，計(jì)算Kk+1，最后計(jì)算解算結(jié)果和Pk+1／k+1,。計(jì)算Kk+1時(shí),，也需要將其分步實(shí)現(xiàn)。若將各步的解算歸于同一個(gè)狀態(tài)機(jī)內(nèi),，則顯得邏輯復(fù)雜,。為使得各步的邏輯更加清晰，并且增加狀態(tài)機(jī)的穩(wěn)定性和安全性,，使用交互狀態(tài)機(jī),，如圖2所示。



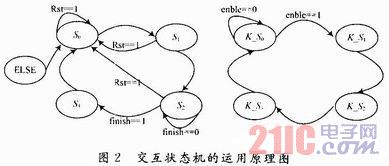
圖2中,，狀態(tài)機(jī)的交互過程中,，沒置標(biāo)志信號enble和finish分別用于啟動(dòng)和終止計(jì)算K值的狀態(tài)，初始化時(shí)其值均為0,。當(dāng)計(jì)算完第一步進(jìn)入S2時(shí),，enble置為1,，啟動(dòng)計(jì)算K值的狀態(tài)；當(dāng)K值計(jì)算完成時(shí),，finish置為1,，進(jìn)入S3，enble和finish置為初值0,，為下次狀態(tài)交互做準(zhǔn)備,。進(jìn)入原狀態(tài)機(jī)繼續(xù)進(jìn)行下面的計(jì)算。

書寫狀態(tài)機(jī)時(shí),，采用三段式寫法,，一個(gè)模塊采用同步時(shí)序描述狀態(tài)轉(zhuǎn)移，另一個(gè)模塊采用組合邏輯判斷轉(zhuǎn)移條件并進(jìn)行狀態(tài)轉(zhuǎn)移,，第三個(gè)模塊實(shí)現(xiàn)同步輸出,。三段式描述方法的狀態(tài)機(jī)，做到了同步寄存器輸出,，消除了組合邏輯輸出的不穩(wěn)定和毛刺現(xiàn)象,，而且更利于時(shí)序路徑分組，綜合與布局布線效果更佳,。

2．3 資源分時(shí)復(fù)用

FPGA設(shè)計(jì)中,，資源與速度是個(gè)矛盾體,。FPGA中的資源是有限的,，所以必須考慮資源的節(jié)省問題。由于Kalman濾波可以分3步進(jìn)行,，所以每一步可以利用其它步中相同的資源,。此種方法可以在不降低總體速度的情況下，減少資源利用量,；而對于階次較高的Kalman濾波,，此方法可以最大限度的增加并行性，提高速度,。該設(shè)計(jì)中用到大量的乘法器,、加法器以及CLB等資源，計(jì)算第一步時(shí)用到的資源會(huì)在第二步和第三步中用到,，即同一資源被用到3次,。以其中用到的某乘法器的分時(shí)復(fù)用為例，其輸入端口在不同的時(shí)刻可以有不同的賦值,，實(shí)現(xiàn)語句如下：



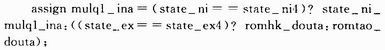
3 性能對比及分析

為驗(yàn)證本文研究利用FPGA實(shí)現(xiàn)Kalman濾波算法的性能,，采用二階Kalman濾波器進(jìn)行實(shí)際性能對比測試。建立數(shù)學(xué)模型如下：選取狀態(tài)轉(zhuǎn)移矩陣,，無控制量,，即控制陣Uk=0,，噪聲系數(shù)矩陣，Wk是系統(tǒng)動(dòng)態(tài)噪聲,，是均值為0,、方差陣為的白噪聲隨機(jī)序列。

對于該濾波器分別利用三種方式實(shí)現(xiàn)：采用Matlab在PC機(jī)上實(shí)現(xiàn),、利用DSP實(shí)現(xiàn)和利用FPGA實(shí)現(xiàn),。其中，PC機(jī)為DELL Dimension4700臺式機(jī),，安裝Matlab 7．0軟件,；DSP選用雙精度浮點(diǎn)型TMS320C6713型號的芯片；FPGA型號為XC2VP30,，主頻100 MHz,，內(nèi)嵌多達(dá)136個(gè)硬核乘法器和2 MB硬件RAM。為得到更準(zhǔn)確合理的結(jié)果,，分別截取第1～3次,、11～13次、21～23次的計(jì)算結(jié)果來對比,。因?yàn)樵赑C機(jī)上利用Matlab實(shí)現(xiàn)的Kalman濾波器通過軟件設(shè)置可以達(dá)到很高的計(jì)算精度,，所以將其得到的結(jié)果作為標(biāo)準(zhǔn)值(真值)，分別用FPGA實(shí)現(xiàn)和DSP實(shí)現(xiàn)的結(jié)果與其進(jìn)行對比分析,。選取估計(jì)均方誤差陣Pk+1／k+1的第一個(gè)元素來進(jìn)行對比分析各實(shí)現(xiàn)方式的性能,，其解算結(jié)果對比如表2和表3所示。



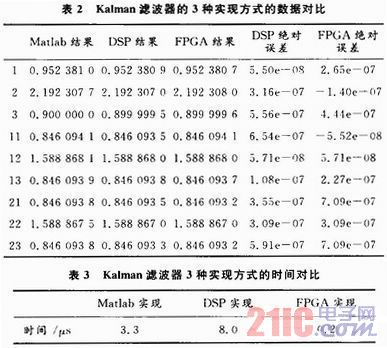
由表2可知,，利用FPGA實(shí)現(xiàn)的濾波結(jié)果,，其精度與用Matlab實(shí)現(xiàn)的精度相差無幾，且略高于利用DSP實(shí)現(xiàn)的單精度的結(jié)果,。由表3可知,，在解算時(shí)間方面，利用FPGA實(shí)現(xiàn)方式的快速性遠(yuǎn)遠(yuǎn)高于利用其他兩種方式,。而且,，對于階次越高的Kalman濾波器的實(shí)現(xiàn)，傳統(tǒng)處理器所需的時(shí)間越長,，利用FPGA實(shí)現(xiàn)方式的時(shí)間的優(yōu)越性越顯著,。

4 結(jié)語

針對Kalman濾波的傳統(tǒng)實(shí)現(xiàn)方法的不足，本文提出利用具有可并行計(jì)算特點(diǎn)的FPGA來實(shí)現(xiàn)Kalman濾波的方案,，并對FPGA實(shí)現(xiàn)Kalman濾波的三種方式進(jìn)行了研究,，確定了利用IP核作為主要計(jì)算元件的實(shí)現(xiàn)方式。對Kalman濾波實(shí)現(xiàn)過程中的關(guān)鍵問題進(jìn)行了研究和實(shí)現(xiàn)。通過對PC機(jī),、DSP和FPGA三種實(shí)現(xiàn)方式的結(jié)果對比,，驗(yàn)證了利用FGPA實(shí)現(xiàn)的Kalman濾波器具有較高的精度和極高的實(shí)時(shí)性。