摘 要： 分析了變步長(zhǎng)LMS算法自適應(yīng)濾波器基本原理,，使用MATLAB對(duì)其進(jìn)行仿真,，并應(yīng)用SZ-EPP5402評(píng)估板進(jìn)行了DSP實(shí)現(xiàn)，結(jié)果表明,，變步長(zhǎng)LMS算法能夠克服固定步長(zhǎng)LMS算法的矛盾,，具有較快收斂速度與較小穩(wěn)態(tài)誤差。
??? 關(guān)鍵詞： LMS算法,；自適應(yīng)濾波器,；DSP
?
?? 在數(shù)字信號(hào)處理中，濾波技術(shù)占有極其重要的地位,。自適應(yīng)濾波器是利用前一時(shí)刻已獲得的濾波器參數(shù),，自動(dòng)地調(diào)節(jié)、更新現(xiàn)時(shí)刻的濾波器參數(shù),，以適應(yīng)信號(hào)和噪聲未知的統(tǒng)計(jì)特性,，從而實(shí)現(xiàn)最優(yōu)濾波[1]。當(dāng)在未知統(tǒng)計(jì)特性的環(huán)境下處理觀測(cè)信號(hào)時(shí),，利用自適應(yīng)濾波器可以獲得令人滿(mǎn)意的效果,，其性能遠(yuǎn)超過(guò)通用方法所設(shè)計(jì)的固定參數(shù)濾波器。在通信,、雷達(dá),、聲納、控制工程及生物醫(yī)學(xué)等領(lǐng)域應(yīng)用廣泛,。
選擇DSP完成自適應(yīng)濾波器的設(shè)計(jì),，具有穩(wěn)定性好、精確度高,、不受環(huán)境影響,、靈活性好等優(yōu)點(diǎn)。固定步長(zhǎng)LMS算法濾波器在收斂速度與穩(wěn)態(tài)誤差之間存在矛盾,，加快收斂速度的同時(shí)也會(huì)增大穩(wěn)態(tài)誤差,。本文使用變步長(zhǎng)LMS算法對(duì)其進(jìn)行改進(jìn)，在TMS320C5402DSP芯片上實(shí)現(xiàn)了基于固定步長(zhǎng)與變步長(zhǎng)LMS算法的自適應(yīng)濾波器,，結(jié)果表明,，變步長(zhǎng)LMS算法自適應(yīng)濾波器性能得到明顯改善,，在加大其收斂速度的同時(shí)也很好地減小了穩(wěn)態(tài)誤差。
1? 自適應(yīng)濾波器基本結(jié)構(gòu)和LMS算法???
1.1? 自適應(yīng)濾波器基本結(jié)構(gòu)
自適應(yīng)濾波器由2個(gè)分離的部分組成[2]：(1)濾波器,，為完成期望的處理功能而設(shè)計(jì),；(2)自適應(yīng)算法，調(diào)節(jié)濾波器系數(shù),，以改進(jìn)性能,。自適應(yīng)橫向型濾波器的結(jié)構(gòu)如圖1所示。圖1中x(n)為輸入信號(hào),，通過(guò)權(quán)系數(shù)可調(diào)的數(shù)字濾波器產(chǎn)生輸出信號(hào)y(n),，將y(n)與期望信號(hào)d(n)進(jìn)行比較，得到誤差信號(hào)e(n),。e(n)和x(n)通過(guò)自適應(yīng)算法對(duì)濾波器參數(shù)進(jìn)行調(diào)整,，按照某種算法準(zhǔn)則判斷誤差信號(hào)e(n)是否達(dá)到最小。重復(fù)以上過(guò)程,，濾波器逐漸掌握了輸入信號(hào)與噪聲規(guī)律,，以此為依據(jù)調(diào)節(jié)自身參數(shù)，達(dá)到最佳濾波效果,。令W(n)為圖1中濾波器系數(shù)矢量,，即W(n)=[W0(n)，W1(n),，…,，WN(n)]，則自適應(yīng)濾波器的輸出為：
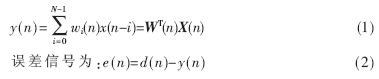
1.2? LMS算法
最常用的判斷e(n)的準(zhǔn)則為最小均方算法,，即LMS算法,。算法的目標(biāo)是通過(guò)調(diào)整系數(shù)，使輸出誤差序列e(n)=d(n)-y(n)的均方值最小化,，并且根據(jù)這個(gè)判據(jù)來(lái)修改權(quán)系數(shù)[3],。其中誤差序列的均方值又叫“均方誤差”MSE(Mean Square Error)，即：
目標(biāo)函數(shù)ε是W的二次函數(shù),，形成一個(gè)碗狀拋物面(性能曲面),，此曲面有唯一最低點(diǎn)即為碗底最小點(diǎn)，自適應(yīng)濾波系數(shù)的起始值位于曲面的某一點(diǎn),，經(jīng)過(guò)自適應(yīng)調(diào)節(jié),，濾波系數(shù)變化，向碗底最小點(diǎn)移動(dòng),，最終到達(dá)最小點(diǎn)[4]。系數(shù)變化按照梯度負(fù)方向移動(dòng)達(dá)到最小點(diǎn)的速度最快,，令▽(n)表示n時(shí)刻的N×1維梯度矢量,，N是濾波器系數(shù)個(gè)數(shù),，自適應(yīng)濾波器系數(shù)矢量的變化與梯度的關(guān)系為：
???
將式(7)代入式(6)得到：
初始收斂速度與穩(wěn)態(tài)誤差是衡量自適應(yīng)濾波算法優(yōu)劣的2個(gè)重要技術(shù)指標(biāo)[5]。減小步長(zhǎng)μ可減小自適應(yīng)算法的穩(wěn)態(tài)誤差,，但卻減慢了算法初始收斂速度,；增大步長(zhǎng)μ可加快算法收斂速度，但卻增大了穩(wěn)態(tài)誤差,。因此,，固定步長(zhǎng)LMS算法在加快算法初始收斂速度與減小穩(wěn)態(tài)誤差之間存在矛盾。
2?變步長(zhǎng)LMS算法
??? 為了克服固定步長(zhǎng)LMS算法收斂速度與穩(wěn)態(tài)誤差之間的矛盾,，提出變步長(zhǎng)LMS自適應(yīng)算法,。即在初始階段選用較大步長(zhǎng)，使算法有較快初始收斂速度,，隨著收斂加深之后采用較小步長(zhǎng)來(lái)減小穩(wěn)態(tài)誤差,。本文中變步長(zhǎng)μ公式為：
在變步長(zhǎng)LMS算法中，由于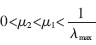
,，在此范圍內(nèi),，變步長(zhǎng)LMS算法得以收斂，而由于μ(n)是變化的,，在初始階段選用較大步長(zhǎng)μ1,，使得變步長(zhǎng)LMS算法比固定步長(zhǎng)LMS算法具有更快的收斂速度。當(dāng)算法逐漸進(jìn)入收斂穩(wěn)定時(shí),，選用較小步長(zhǎng)μ2,，使穩(wěn)態(tài)誤差隨步長(zhǎng)減小而減小，因此,，變步長(zhǎng)LMS算法具有比固定步長(zhǎng)LMS算法更小的穩(wěn)態(tài)誤差,。
3?自適應(yīng)濾波器的MATLAB仿真
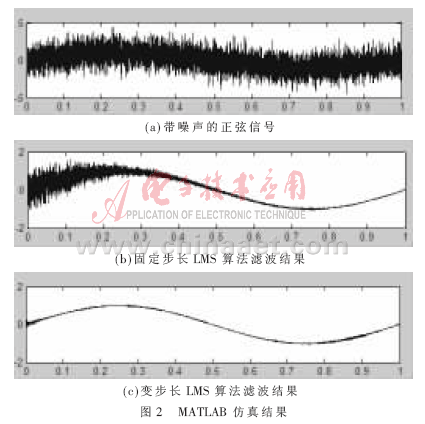
??? 實(shí)驗(yàn)中，設(shè)計(jì)一個(gè)簡(jiǎn)單二階加權(quán)自適應(yīng)橫向?yàn)V波器,，用單頻正弦信號(hào)與一個(gè)隨機(jī)噪聲進(jìn)行疊加作為系統(tǒng)輸入信號(hào)x(n),，選取1 000個(gè)采樣點(diǎn)，根據(jù)自適應(yīng)濾波器迭代方程設(shè)計(jì)自適應(yīng)濾波器,，對(duì)輸入信號(hào)x(n)進(jìn)行濾波,。固定步長(zhǎng)LMS算法選用步長(zhǎng)μ為0.002 6，變步長(zhǎng)LMS算法在算法初始300個(gè)采樣點(diǎn)時(shí)選取μ1為0.004 2,，在算法初始收斂逐漸加深后,，后面700個(gè)采樣點(diǎn)選取μ2為0.002 1。仿真結(jié)果如圖2所示,。
??? 從圖2(b)中可以看出,，固定步長(zhǎng)LMS算法濾波結(jié)果在開(kāi)始階段收斂速度比較慢，有較大穩(wěn)態(tài)誤差,，算法有待改善,。圖2(c)中變步長(zhǎng)LMS算法濾波結(jié)果比固定步長(zhǎng)LMS算法具有更快初始收斂速度與較小穩(wěn)態(tài)誤差,，濾波效果得到明顯改善，濾波性能優(yōu)于固定步長(zhǎng)LMS算法,。從仿真角度證明了變步長(zhǎng)LMS算法的優(yōu)越性與可行性,。
4?自適應(yīng)濾波器的DSP實(shí)現(xiàn)
為了提高LMS算法的處理速度且減小系統(tǒng)硬件規(guī)模，采用TI公司的TMS320C5402芯片作為核心芯片實(shí)現(xiàn)該算法,。該處理器采用程序與數(shù)據(jù)分開(kāi)的哈佛體系結(jié)構(gòu),，片上有16 KB存儲(chǔ)器，外部擴(kuò)展32 KB的數(shù)據(jù)存儲(chǔ)器,，64 KB的程序存儲(chǔ)器,；具有高度并行性。用C語(yǔ)言實(shí)現(xiàn)變步長(zhǎng)LMS算法子程序流程如圖3所示,。其中,，N為迭代次數(shù)；order為階數(shù),；μ1,、μ2為步長(zhǎng)；count為當(dāng)前采樣點(diǎn),；NS為采樣點(diǎn)數(shù),。
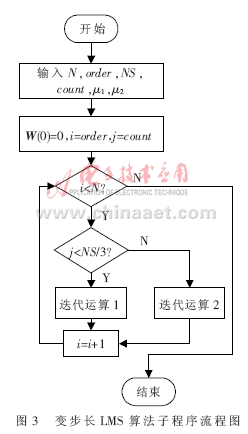
在圖3中，首先輸入濾波器迭代次數(shù)N,，步長(zhǎng)μ1,、μ2，采樣點(diǎn)數(shù)NS的值,，初始化濾波器系數(shù)矢量W(0)為零,，定義2個(gè)指針i、j,，分別指向?yàn)V波器系數(shù)階數(shù)order與當(dāng)前采樣點(diǎn)數(shù)count,，當(dāng)階數(shù)小于迭代次數(shù)N，且采樣點(diǎn)數(shù)小于總采樣點(diǎn)數(shù)的1/3時(shí),，進(jìn)行迭代運(yùn)算1,，此時(shí)步長(zhǎng)為μ1；大于1/3時(shí),，進(jìn)行迭代運(yùn)算2,，步長(zhǎng)為μ2。
??? 設(shè)計(jì)中,，采用1 500 Hz的期望信號(hào)與312 Hz的噪聲信號(hào)疊加作為30個(gè)系數(shù)的自適應(yīng)濾波器的一個(gè)輸入信號(hào),，對(duì)于每一個(gè)時(shí)刻n，計(jì)算自適應(yīng)濾波器的輸出，誤差信號(hào)是輸出信號(hào)與期望信號(hào)的差值,。固定步長(zhǎng)LMS算法與變步長(zhǎng)LMS算法在SZ-EPP5402評(píng)估板上實(shí)現(xiàn)的結(jié)果如圖4所示,。
?? 從圖4(b)中可以看出，在濾波初始階段,，濾波結(jié)果不明顯，輸入的疊加信號(hào)經(jīng)過(guò)自適應(yīng)濾波器后,，在初始階段噪聲沒(méi)有得到明顯抑制,，存在較大穩(wěn)態(tài)誤差，收斂速度比較慢,，收斂速度和穩(wěn)態(tài)誤差都有待改善,。從圖4(c)中可以看出，在濾波初始階段,，穩(wěn)態(tài)誤差已得到明顯改善,，有較小穩(wěn)態(tài)誤差，初始收斂速度也有所加快,，輸入的疊加信號(hào)經(jīng)過(guò)自適應(yīng)濾波器后,，噪聲得到明顯抑制，濾波性能明顯優(yōu)于固定步長(zhǎng)LMS算法,，具有較快收斂速度與較小穩(wěn)態(tài)誤差,，很好地克服了固定步長(zhǎng)存在的矛盾。
初始收斂速度與穩(wěn)態(tài)誤差是衡量自適應(yīng)濾波算法性能優(yōu)劣的2個(gè)重要技術(shù)指標(biāo),。本文通過(guò)對(duì)固定步長(zhǎng)和變步長(zhǎng)LMS算法自適應(yīng)濾波器進(jìn)行MATLAB仿真與DSP實(shí)現(xiàn),，比較二者結(jié)果，證明了變步長(zhǎng)LMS算法能夠保證較快的收斂速度與較小的穩(wěn)態(tài)誤差,，并能有效去除不相關(guān)的獨(dú)立噪聲干擾,，克服固定步長(zhǎng)在增大初始收斂速度與減小穩(wěn)態(tài)誤差之間存在的矛盾，優(yōu)化了自適應(yīng)濾波器的性能,，濾波效果明顯,。
參考文獻(xiàn)
[1] SHIREEN W， TAO L I.A DSP-based active power filter for low voltage distribution systems[J].Electric Power
Systems Research,，2008,，78：1561-1567.
[2] 呂振肅，熊景松.一種改進(jìn)的變步長(zhǎng)LMS自適應(yīng)算法[J].信號(hào)處理,，2008,，24(1)：144-146.
[3] KUKRER O，HOCANIN A.Frequency-response-shaped LMS adaptive filter[J].Digital Signal Processing,，2006,，
16：855-869.
[4] 葉永生，余容桂，吳霄.一種新的自適應(yīng)最小均方算法及其應(yīng)用研究[J].電測(cè)與儀表,，2008,，45(7)：19-22.
[5] 張會(huì)生，閆學(xué)斌,，秦勇,，等.LMS算法自適應(yīng)濾波器的DSP實(shí)現(xiàn)[J].通信技術(shù)，2006(10)：72-73.