摘  要： 提出了一種確定圖片重疊區(qū)域的通用算法,。首先將兩幅圖片重疊部分的頂點存入一個交點數(shù)組,，然后再分別將兩幅圖像的頂點與交點數(shù)組中的點進行比較，若交點數(shù)組中的點完全是其中一幅圖的頂點,，則該圖即為重疊區(qū)域,；否則，必須按照一定的算法來確定重疊區(qū)域,。實驗結(jié)果表明,，該算法在易于編程實現(xiàn)的同時，也能很好地確定出影像間的重疊區(qū)域,，并且適合確定多張影像的重疊區(qū)域,。
關(guān)鍵詞： 重疊區(qū)域；求交,；多邊形,；數(shù)組；圖像

　圖像拼接技術(shù)是將一組存在重疊部分的圖像序列進行空間匹配對準,，經(jīng)重采樣融合后形成一幅包含各圖像序列信息的寬視角場景,、完整、高清晰的新圖像的技術(shù)[1],。該技術(shù)廣泛應(yīng)用在攝影測量學(xué),、虛擬現(xiàn)實技術(shù)、遙感影像處理,、醫(yī)學(xué)圖像分析和計算機圖形學(xué)等領(lǐng)域,。
　一般來說，圖像拼接流程包括圖像預(yù)處理,、圖像配準和圖像合成三個步驟,。在進行多幅圖像的拼接時,，首先應(yīng)確定標(biāo)準像幅，標(biāo)準像幅往往選擇處于研究區(qū)中央的圖像,，以后的拼接工作都以此圖像作為基準進行,；其次確定拼接的順序，即以標(biāo)準像幅為中心,，由中央向四周逐步進行,。值得注意的是，拼接工作的著眼點是全部待拼接的圖像,，而落腳點卻總是兩幅相鄰圖像間的拼接,。遙感圖像拼接工作主要是基于相鄰圖像的重疊區(qū)，無論是色調(diào)調(diào)整還是幾何鑲嵌,，都是將重疊區(qū)域作為基準進行的,。重疊區(qū)域的確定是否準確，直接影響拼接的效果[2],。本文結(jié)合計算機圖形學(xué)的知識,，提出了一種確定自由像片重疊區(qū)域的算法。實驗結(jié)果表明,，該算法適合對多張影像進行重疊區(qū)域的確定,。
1 圖像配準
　圖像配準主要指對參考圖像和待拼接圖像中的匹配進行提取，在提取出的信息中尋找最佳的匹配,，完成圖像間的對齊[1],。
　本文通過仿射變換進行圖像配準，配準后自由像片重疊區(qū)域的確定問題就轉(zhuǎn)化為多邊形重疊區(qū)域的確定問題,，即兩個或多個面求交集的問題,。因攝影過程中像片的自由度較大，重疊部分可能是三邊形,、四邊形,，甚至是八邊形，故確定多邊形的重疊區(qū)域?qū)⑹且粋€較為復(fù)雜的過程,，同時也增加了數(shù)據(jù)處理的難度。下面結(jié)合計算機圖形學(xué)的知識研究有關(guān)該問題的一種通用算法[3],。
2 確定多邊形重疊區(qū)域的理論基礎(chǔ)
　簡單多邊形的一般定義是指不自相交的多邊形,，它可以包含0個或多個空洞。確定兩個任意多邊形交,、并,、差的問題既是計算幾何和計算機圖形學(xué)的基本問題，也是遙感影像處理,、GIS疊加分析的理論基礎(chǔ)[4],。本文討論的是比較簡單的凸多邊形的情況,。
在幾何造型中，通常利用集合運算(交,、并,、差運算)實現(xiàn)復(fù)雜形體的構(gòu)造，而集合運算需要大量的求交運算,。求交時所用到的幾何元素大致可分為三類：點,、線、面,。故在求交算法中,，求交方法分為點點、點線,、點面,、線線、線面,、面面六種,。常用的求交有線與線的求交、線與面的求交和面與面的求交,。多邊形與多邊形,，即面與面之間的求交是最為復(fù)雜的一種。面與面求交的基本方法主要有代數(shù)方法,、幾何方法,、離散方法和跟蹤方法四種[5]。本文主要運用跟蹤方法來實現(xiàn)多邊形的求交,。該方法是通過先求出初始交點,，然后從已知的初始交點出發(fā)，相繼跟蹤計算出下一交點,，從而求出整條交線的方法,。其中，跟蹤法的初始交點通常采用離散方法求得,。
3 確定多邊形重疊區(qū)域的算法流程
　自由像片重疊區(qū)域的確定為以后進行圖像拼接奠定了良好的基礎(chǔ),。因此有必要對多邊形重疊區(qū)域的確定問題進行詳細的研究。圖像的重疊部分可以是規(guī)則的,，也可以是不規(guī)則的,，可以是由三條邊所圍成的圖像，也可以是由四條邊甚至更多條邊所圍成的圖像,。為了確定多邊形的重疊區(qū)域,，本文以相對比較簡單且規(guī)則的四邊形為例來進行討論。設(shè)有兩個四邊形A={a1,，a2,，a3,，a4}，B={b1,，b2,，b3，b4},，其中ai,、bi(i=1、2,、3,、4)分別為四邊形A與B的頂點。兩頂點間的直線分別用Li,、Ri表示(i為較小頂點標(biāo)號),，兩個四邊形邊的交點表示為Pij，其中i為左線段序號,，j為右線段序號,。兩四邊形的交集為P=A∩B={k|k∈A∧k∈B}，此交集即為重疊區(qū)域,。
通過分析,，對由兩幅圖像的重疊部分所構(gòu)成的多邊形區(qū)域進行以下幾種情況的討論，重疊區(qū)域的頂點坐標(biāo)可通過計算獲得,，并存儲在交點數(shù)組P[n]中,。
　(1)所構(gòu)成的多邊形區(qū)域只包含圖A的頂點。此時,，P[n]中的點完全屬于圖A的頂點,，則圖B完全覆蓋圖A，圖A為所求的重疊區(qū)域,，如圖1所示,。

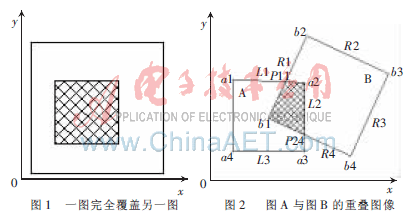
　(2)所構(gòu)成的多邊形區(qū)域只包含圖B的頂點。此時,，P[n]中的點完全屬于圖B,，則圖A完全覆蓋圖B，圖B為所求的重疊區(qū)域,，如圖1所示,。
　(3)所構(gòu)成的多邊形區(qū)域由圖A和圖B邊的交點構(gòu)成。此時,，P[n]中的點既有圖像A的頂點又有圖像B的頂點，還包含有圖像A與圖像B的邊的交點,，則按照下述方法來確定重疊區(qū)域：首先找出一個交點,，然后沿其中一條邊(重疊區(qū)域邊)的方向行進,。由L1可以找到頂點a2，再沿著L2找到P24,，此時要更換交點的追蹤邊,，然后轉(zhuǎn)換到R4邊上，找到b1點,。依此進行,，直到最后的邊R1剛好與P11的R1邊連接，形成一個閉合區(qū)域,，如圖2所示,。
確定多邊形重疊區(qū)域的算法流程如圖3所示。

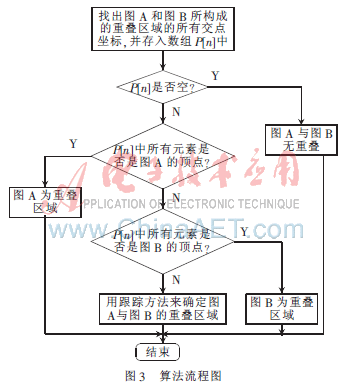
4 確定多邊形重疊區(qū)域的算法描述
　為了查找圖A與圖B的重疊區(qū)域,，可以先將兩幅圖的頂點坐標(biāo)分別存入數(shù)組A-Point[n]和數(shù)組B-Point[n]中,，并定義一個交點數(shù)組P[n]。該數(shù)組用來存放由圖A和圖B所構(gòu)成的重疊區(qū)域的所有交點,。其中,，存儲圖A和圖B各頂點的橫、縱坐標(biāo)以及交點數(shù)組P[n]的橫,、縱坐標(biāo)的數(shù)據(jù)結(jié)構(gòu)可分別設(shè)計如下：
Typedef stu{
        Int x,，y；//圖A各頂點的橫,、縱坐標(biāo),；
} A-Point；
Typedef stu{
        Int x,，y,； //圖B各頂點的橫、縱坐標(biāo),；
} B-Point,；
Typedef stu{
        Int x，y,； //數(shù)組P[n]各頂點的橫,、縱坐標(biāo)；
} P-Point,；
確定圖A與圖B的重疊區(qū)域的算法如下：
If  P[n]!=null  then
        If P[n]中的點都是圖像A的頂點 then
         Cout<<“圖像A為所求的重疊區(qū)域”,；
//圖B完全覆蓋圖A
Else
         If  P[n]中的交點都是圖像B的頂點 then
             Cout<<“圖B為所求的重疊區(qū)域”；
//圖A完全覆蓋圖B
         Else
            //圖A與圖B有交叉,，用跟蹤方法來確定多邊形
//的重疊區(qū)域
            Do
             { 找出圖A與圖B的一個交點,，然后沿著交點所在邊的方向行進順次找下一個交點，并轉(zhuǎn)換追蹤邊直至閉合；
             }
            While (P[n]= =null)
        Endif
  Endif
Else
    Cout<<“圖A與圖B無重疊區(qū)域”,；
//圖A與圖B不相交
Endif
Return 0,； //結(jié)束
　上述算法中，判斷交點數(shù)組中的所有點是否完全是圖A或圖B的頂點的方法大致有兩種：
(1)將P[n]中的每個點的橫,、縱坐標(biāo)與圖A或圖B的各個頂點的橫,、縱坐標(biāo)相比較，若它們的橫,、縱坐標(biāo)值完全相同,，則一幅圖完全覆蓋另一幅圖。
　(2)判斷交點數(shù)組P[n]中的所有點是否是圖A或圖B的內(nèi)點,。若P[n]中的所有點都是圖A的內(nèi)點,，則圖A完全覆蓋圖B，圖B為重疊區(qū)域,；若P[n]中的所有點都是圖B的內(nèi)點,，則圖B完全覆蓋圖A，圖A為重疊區(qū)域(注：因點與多邊形的位置關(guān)系有三種,，即：點在多邊形內(nèi),、點在多邊形上、點在多邊形外,。故本文把在多邊形內(nèi)的點簡稱為內(nèi)點,，在多邊形外的點簡稱為外點)。
　本文是在計算機圖形學(xué)的基礎(chǔ)上進行研究的,，通過對多邊形重疊區(qū)域的分析總結(jié)出圖像與圖像之間重疊區(qū)域的確定問題,。該算法已用VC++語言實現(xiàn)，現(xiàn)給出如圖4,、圖5所示的一個算例的執(zhí)行結(jié)果,，其中圖4為兩個四邊形圖A和圖B，圖5為圖A與圖B的重疊區(qū)域,。

　實踐表明,，此種確定多邊形重疊區(qū)域的算法具有很好的實驗結(jié)果，算法結(jié)構(gòu)清晰易懂,，易于編程實現(xiàn),。需要說明的是，該算法雖然也可以同時對多張(大于兩張)自由像片的重疊區(qū)域進行確定,，但隨著像片數(shù)量的增多,，其處理速度也會降低。此問題也有待于今后進一步地探討和研究,。
參考文獻
[1] 陳挺.圖像拼接算法及實現(xiàn)[EB/OL].http：//www.studa.net/yingyong/090603/1636506.html,，2009-06/2010-04.
[2] 黃曉萍.基礎(chǔ)地理信息工程[EB/OL].http：//course.cug.edu.cn/cugThird/base_MAPGIS/classroom/5-3-1.htm，2002-3/2010-04.
[3] 王悅，吳云東,，張魁珂,，等.自由像片重疊區(qū)域的確定及拼接[J].海洋測繪，2008,，28(5)：1-4.
[4] 朱雅音，王化文,，萬豐,，等．確定兩個任意簡單多邊形交、并,、差的算法[J]．計算機研究與發(fā)展,，2003，40(4)：1-8.
[5] 和青芳.計算機圖形學(xué)原理及算法教程(Visual C++)[M/CD].http：//wenku.baidu.com/view/bb4117661ed9ad51f01df27d.html,， 2010.02.15／2010.04.06.