在多路實時語音處理系統(tǒng)中，基于高斯混合概率模型[1,，2]的系統(tǒng)后端運算量非常大,，采用log-add算法單元可以簡化運算，提高運算效率,。其函數(shù)形式為[3]：

   查表法可以認為是多項式次數(shù)為0的情況,，隨著精度要求的增加，查找表會變得很大[5],。函數(shù)逼近可以采用多項式擬合,，首先根據(jù)所需要的精度確定多項式次數(shù)和分段的大小，然后計算每一段的多項式系數(shù),。
    設分段的大小為d(d=2-k,，k=0，1,，2…),，計算各段系數(shù)時，各段函數(shù)平移到區(qū)間[0,，d）,，如圖2所示。用Matlab進行多項式擬合依次得到各段系數(shù)。由此可以得出各段的擬合多項式為：

    這樣實現(xiàn)時可以把二進制的定點數(shù)x分為MSBs和LSBs兩段,。MSBs對應段標號i,，由段標號取出系數(shù)ci0，ci1,，ci2…,；LSBs對應浮點數(shù)xl，代表段內(nèi)偏移值,。由圖3可以計算出f(x),。

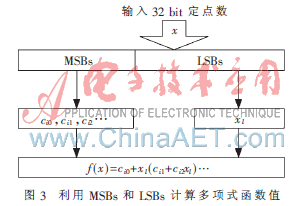
    MSBs和LSBs應該這樣選取，例如定標為Q32.f,，選擇d=1/2,，則MSBs為高32-（f-1）位，LSBs為低f-1位,；選擇d=1/4, 則MSBs為高32-(f-2)位,，LSBs為低f-2位……；如果MSBs為32或31,，則變成了查表法,。
2 多項式擬合的實現(xiàn)方案
2.1 多項式次數(shù)與分段大小、精度的關系
    用Matlab進行仿真,，表1列出了各種精度要求下各次多項式所需的分段大小(d),，其中?啄為精度要求，?茁為多項式的次數(shù),。
    由表1可以看出,，相同次數(shù)的情況下，精度要求越高,，分段大小d越?。欢嗤鹊那闆r下,，次數(shù)越高,，分段大小d越大。另外,，次數(shù)越低，精度越高,，分段大小d下降的數(shù)量級越快,。

    表2列出各次多項式在不同精度要求下，所需要系數(shù)個數(shù)(n)的分布情況,。

    由表2可以看出,，其結果與表1趨于一致。相同次數(shù)下,，精度要求越高,，所需要的系數(shù)個數(shù)n越多,；而相同精度下，次數(shù)越高,，所需要系數(shù)個數(shù)n越少,。n隨著次數(shù)的降低和精度的提高迅速增大。
    與n相反,，多項式的計算量隨著多項式次數(shù)的增加而增加,。根據(jù)horner算法[3]多項式的表達式如下：
  
    式(6)表明，多項式次數(shù)增加1次,，計算多項式的函數(shù)值增加1次乘法和1次加法,。多項式系數(shù)存儲量與多項式的計算量是其FPGA實現(xiàn)時互相制約的兩個因素。
3 仿真結果
    為了取得面積與速度的平衡,，根據(jù)測試結果及實際系統(tǒng)的要求,，選擇δ=10-4、β=1來實現(xiàn),。本文采用Xilinx ISE Design Suite 10.1進行仿真測試,。定標取Q32.23，其硬件實現(xiàn)計算流程如圖4,，輸入為定點數(shù)x,，由MSBs和LBSs取得系數(shù)和xl，經(jīng)過reg系數(shù)寄存器及1次乘法和1次加法,，輸出y,。

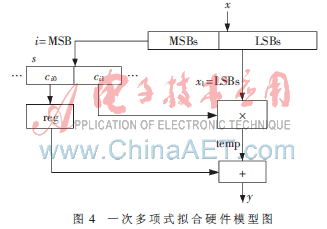
    時序仿真結果結果如圖5。輸入x是32 bit的無符號定點數(shù),，輸出為y,；clk是時鐘；reset為復位信號,；MSBs是x的高位,，用于得到多項式系數(shù)；LSBs是x的低位即自變量,；temp是用于緩存中間結果,，coef[...]是多項式系數(shù)。輸出延遲3個時鐘周期,，流水線填滿后,，每個時鐘周期輸出一個結果。

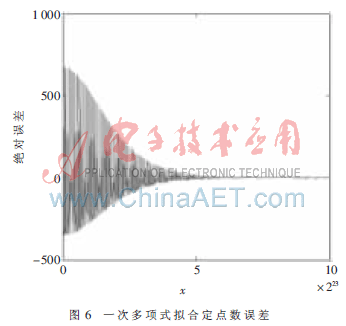
    例如輸入32’h00333333（浮點數(shù)0.4）,，從圖中可以看出其輸出y為24’h41aba5,，與實際函數(shù)值24’h41aa7c存在誤差。其實現(xiàn)結果與浮點結果比較誤差如圖6?？梢钥闯龆c數(shù)誤差在800以內(nèi),，也就是浮點數(shù)約10-4以內(nèi)，誤差范圍與表1相一致,。

    使用ISE軟件的XST工具綜合,，選擇設備為Xilinx公司Virtex5系列的XC5VFX100T(speed-2)。其資源占用情況如表3,，其中Xilinx公司的乘加硬件設備DSP48E用于算法中的乘法運算及加法運算[6],。

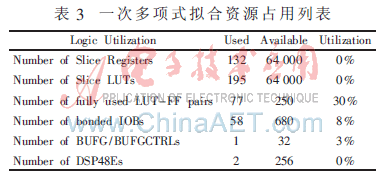
    可以對比δ=10-4，β=0,，1,，2，3四種實現(xiàn)方式的硬件開銷,，如表4,。

    由表4可以看出，雖然多項式次數(shù)為0時使用寄存器（Registers）和查找表（LUTs）最少,，且乘法和加法次數(shù)（DSP48Es）為0,，但由于其使用了24×40 960 ROM，占用存儲面積較大,；而一次多項式擬合雖然所占用查找表(LUTs)一項相對較多,，但綜合考慮，其他資源占用都比較均衡,。其整體的資源開銷要好于其他方案,。
    log-add算法單元作為高斯混合概率模型FPGA實現(xiàn)的基本算法單元，能夠簡化運算,、提高運算效率,。在系統(tǒng)精度要求10-4的情況下，采用一次多項式擬合能夠有效地節(jié)省硬件開銷,，實現(xiàn)簡單快速log-add算法單元,，為大規(guī)模實時處理多路語音數(shù)據(jù)提供了重要保證。
參考文獻
[1] Douglas A.Reynolds,，THOMAS E.Quatieri,，Robert B.Dunn. Speaker verification using adapted gaussian mixture models[J].Digital Signal Processing，2000(10).
[2] Kazuo Miura,，Hiroki Noguchi,，Hiroshi Kawaguchi，et al.A  low memory bandwidth gaussian mixture model(GMM)  processor for 20,，000-word real-time speech recognition FPGA system[J].ICECE Technology，2008.FPT.2008.
[3] MELNIKOFF S J，F(xiàn)QUIGLEY S.Implementing the Log-add  Algorithm in Hardware[J].Electronics Letters,，2003.
[4] LEE B R,，BURGESS N.A pallrallel Look-up logarithmic number system addition subtraction scheme for FPGA[J]. Proc.FPT，2003.
[5] 李煒,，沈緒榜.對數(shù)數(shù)值系統(tǒng)的研究[J].微電子學與計算機,，2004.
[6] 胡彬.Xilinx ISE Design Suite 10.x FPGA開發(fā)指南—邏輯設計篇[M].北京：人民郵電出版社，2008.