用一個(gè)時(shí)間函數(shù)或一條曲線來表示信號(hào)" title="信號(hào)">信號(hào)隨時(shí)間變化的特性,稱為連續(xù)" title="連續(xù)">連續(xù)信號(hào)的時(shí)域" title="時(shí)域">時(shí)域描述" title="描述">描述。在多種多樣的連續(xù)確定性信號(hào)中,有一些信號(hào)可以用常見的基本函數(shù)表示,如正弦函數(shù)、指數(shù)函數(shù)、階躍函數(shù)等,同時(shí)它們還可以組成許多更復(fù)雜的信號(hào),我們把這類信號(hào)稱為基本信號(hào)。討論基本信號(hào)的時(shí)域描述有著重要的意義。通常基本信號(hào)可以分為普通信號(hào)和奇異信號(hào)兩類。
(一) 普通信號(hào)的時(shí)域描述
1.正弦信號(hào)
一個(gè)正弦信號(hào)可表示為
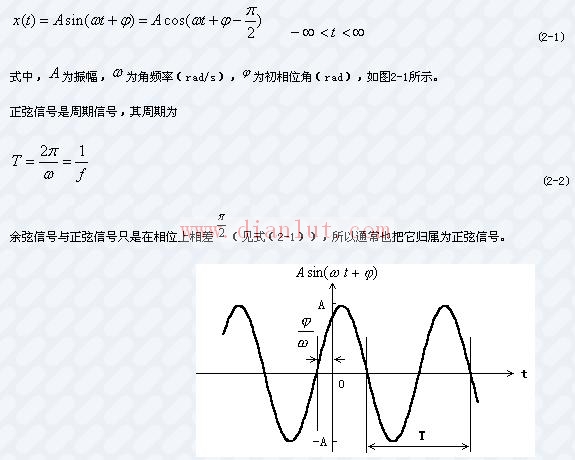
圖2-1 正弦信號(hào)

按歐拉(Euler)公式,復(fù)指數(shù)信號(hào)可以寫成
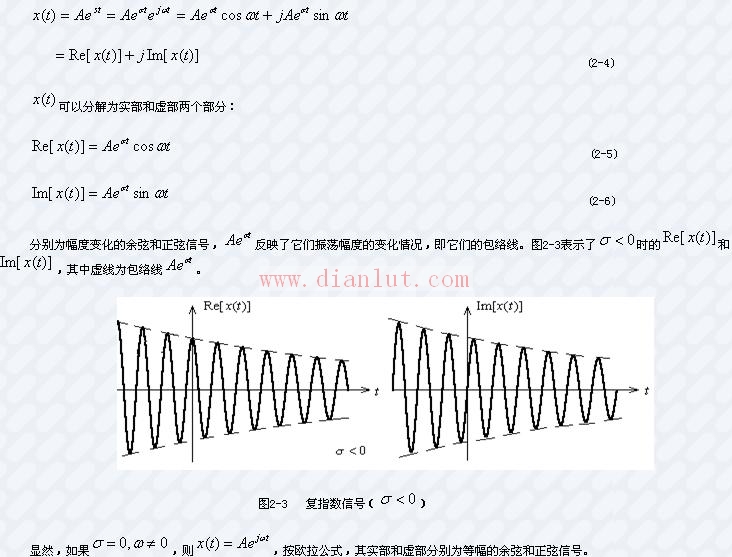
實(shí)際的信號(hào)總是實(shí)的,即都是時(shí)間t的實(shí)函數(shù),復(fù)指數(shù)信號(hào)為復(fù)函數(shù),所以不可能實(shí)際產(chǎn)生。但是一方面如上所述,它的實(shí)部和虛部表示了指數(shù)包絡(luò)的正弦型振蕩,這本身具有一定的實(shí)際意義;其次,它把直流信號(hào)、指數(shù)信號(hào)、正弦型信號(hào)以及具有包絡(luò)線的正弦型信號(hào)表示為統(tǒng)一的形式,并使信號(hào)的數(shù)學(xué)運(yùn)算簡(jiǎn)練和方便,所以在信號(hào)分析理論中具有重要意義。
在信號(hào)的數(shù)學(xué)運(yùn)算中經(jīng)常會(huì)用到如下式子:

(二) 奇異信號(hào)的描述
奇異信號(hào)是用奇異函數(shù)表示的一類特殊的連續(xù)時(shí)間信號(hào),其函數(shù)本身或者函數(shù)的導(dǎo)數(shù)(包括高階導(dǎo)數(shù))具有不連續(xù)點(diǎn)。它們是從實(shí)際信號(hào)中抽象出來的典型信號(hào),在信號(hào)的分析中占有重要的地位。
1.單位斜坡信號(hào)

通過階躍函數(shù),可以表示出如圖2-6所示的矩形脈沖信號(hào)
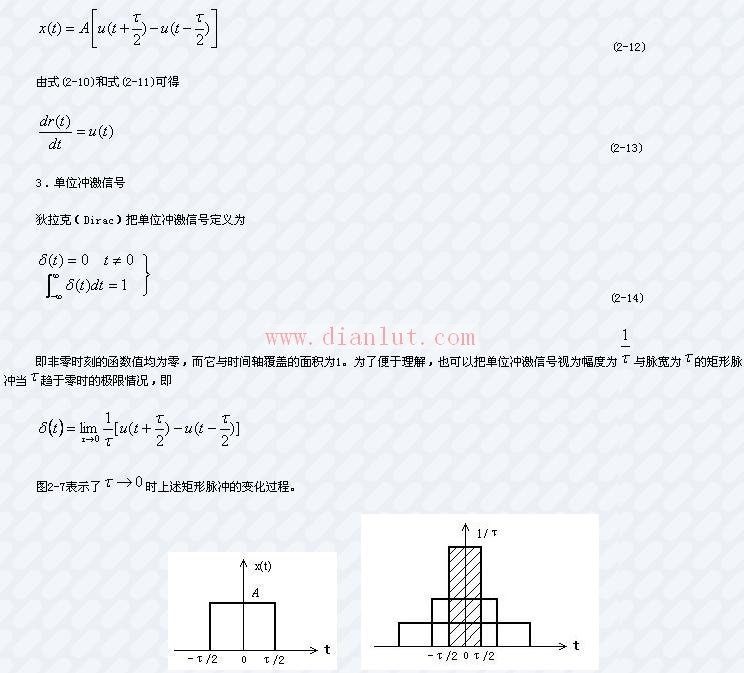
圖2-6 矩形信號(hào) 圖2-7 矩形脈沖向沖激信號(hào)的過渡

再結(jié)合(2-15)式,有


