摘  要： 無功功率計量方法中的移相法有兩種實現(xiàn)方法，一種是基于采樣點平移,，另一種是利用希爾伯特濾波器,。在Matlab上對這兩種方法進行了設計、仿真,，并采用EP2C50型號的FPGA實現(xiàn)了希爾伯特濾波器,。數(shù)據(jù)表明基于采樣點平移的方法有局限性，而希爾伯特移相無功算法具有移相準確的特點,，保證了無功功率的精確計量,。
關(guān)鍵詞： 無功功率；FPGA,；移相法,；Hilbert

    在電力系統(tǒng)運行時,，電網(wǎng)提供的能量有兩部分：一部分是有功功率，用于能量單向轉(zhuǎn)換,；一部分是無功功率,，用于電路內(nèi)電場和磁場的能量交換。無功功率對外不做功,，但是對供電系統(tǒng)和負荷的正常運行十分重要,，在電網(wǎng)中流動會引起電壓和功率損耗。因此,，必須計量電力用戶從電網(wǎng)吸收以及電網(wǎng)傳送的無功功率的大小,。
    移相法是無功功率計量算法中的一種，它是利用無功功率和有功功率之間的相位角相差π/2關(guān)系,，用計算有功功率的乘法器來計算無功功率,。
    本文采用了兩種方法來實現(xiàn)移相法，在Matlab上對這兩種方法進行了設計,、仿真,，并采用EP2C50型號的FPGA實現(xiàn)了希爾伯特濾波器。
1 無功功率與有功功率的關(guān)系
    假設電壓,、電流如式(1),、式(2)所示：
       
 
差值，這是利用移相法計算無功功率的理論依據(jù),，即用計算有功功率的乘法器來計算無功功率,，這在數(shù)字信號處理中十分有用。在實際應用中,，乘法器的兩個輸入序列變成移相后的電壓序列與電流序列就可以實現(xiàn)無功功率計算,。而在計算有功功率時已經(jīng)獲得了電壓的采樣值、 電流的采樣值及電壓電流之間的相位角,，當采樣點數(shù)滿足計算諧波無功電能的奈奎斯特采樣定理時,，針對計算無功功率，有兩種方法可以實現(xiàn)對離散信號的π/2移相：一種是基于采樣點平移來實現(xiàn),；另一種則是通過 Hilbert變換來實現(xiàn)[2],。
2 基于采樣點平移的移相法
    基于采樣點平移的無功計量理論是將得到的離散的采樣點信號進行π/2移相(若N為信號一個周期內(nèi)的采樣點數(shù)，則π/2移相就是移動N/4個點),，然后采用式(3)計算無功功率。如圖1所示,，曲線1是原正弦波信號,；曲線2是基于采樣點平移π/2后的信號，從圖中可以看出,，基于采樣點平移的移相法精確地實現(xiàn)了π/2移相,。

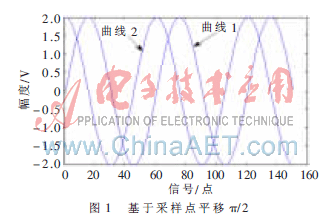
    但是這種方法是針對基波頻率的采樣點移相,，實際應用時有其局限性。
    (1)基于采樣點平移方法要求被采樣的信號只包含基波分量,。假如對一個包含基波和3次諧波的信號(基波的每個周期2π內(nèi))進行100次采樣,，那么基波的π/2移相就是移動25個采樣點，但是,，由于3次諧波的周期縮為基波的1/3,，25個采樣點對于3次諧波而言，已經(jīng)是移相3π/2了,。如圖2所示,，曲線1是原正弦波信號；曲線2是理論上平移π/2后的信號,，曲線3是基于采樣點平移后的信號,， 實際已經(jīng)平移了3π/2。

    (2)基于采樣點平移還要求每個周期的采樣點數(shù)是4的整數(shù)倍,，否則將不能被4整除而得不到π/2的移相,。如圖3所示，曲線1為原正弦波信號,，一個周期內(nèi)采樣點為75,，不是4的整數(shù)倍；曲線2為理論移相π/2的信號,，曲線3為基于采樣點平移的信號,，與曲線2信號對比已有一定的偏移。

    基于采樣點平移的無功計量方法雖然存在其局限性,，但仍被一些要求不高的場合采用,，主要是其實現(xiàn)相對簡單，對硬件的性能要求也不是很高,，但是當電網(wǎng)中的諧波成分提高時,，基于采樣點平移計量無功電能的精度就很難保證[3]。
3 Hilbert變換計算無功功率
3.1 Hilbert數(shù)字濾波器基本原理
    理想的Hilbert變換的定義為：

3.2 FIR型Hilbert數(shù)字濾波器的Matlab設計
    線性相位FIR數(shù)字濾波器的設計方法主要有窗函數(shù)法,、頻率抽樣法和等波紋切比雪夫法(即最優(yōu)法),，本文采用等波紋切比雪夫法進行數(shù)字濾波器的設計。對于50 Hz的工頻基波信號,，若考慮最高諧波次數(shù)為19,，則可以將該數(shù)字濾波器所關(guān)心的頻率范圍設計為40 Hz~960 Hz。根據(jù)奈奎斯特采樣定理,，采樣頻率Fs應不小于2倍的最高次諧波頻率,，所以至少取2 kHz。

    圖4所示為等波紋切比雪夫法設計的Hilbert數(shù)字濾波器的幅頻特性和相頻特性。從圖中可以看出該數(shù)字濾波器具有良好的幅頻特性和相頻特性,，能獲得嚴格線性相位及很好的衰減特性,。

    圖5為頻率為150 Hz的正弦波信號經(jīng)過Hilbert濾波器以后的信號。

   由仿真結(jié)果可知所設計的Hilbert數(shù)字濾波器能精確地將所輸入的電壓諧波信號的基波及每次諧波都移相,，并在此基礎上計算獲得精確的無功功率值,。
3.3 FIR型Hilbert數(shù)字濾波器的FPGA實現(xiàn)
3.3.1 FIR IP核的生成
    Altera公司提供的FIR IP核是一個高性能、參數(shù)化的IP核,，可以用來實現(xiàn)FIR濾波器,。該IP核支持全并行結(jié)構(gòu)、全串行結(jié)構(gòu),、多位串行結(jié)構(gòu),、可變的多時鐘結(jié)構(gòu)等多種結(jié)構(gòu)，濾波器的參數(shù)可以通過該IP 核的參數(shù)化界面進行設計,，也可以將在第三方軟件中設計好的濾波器系數(shù)導入該IP核中從而完成濾波器設計,，它的所有輸入輸出信號格式都與Avalon總線的Streaming結(jié)構(gòu)的接口相符，可以方便地加入到應用工程中,。
    本文中FIR濾波器的實現(xiàn)方法是將Matlab產(chǎn)生的濾波器系數(shù)導入Quartus ii中的FIR IP CORE中,。圖6是Quartus生成的FIR IP核。

3.3.2 FIR IP核的的驗證
    由于所設計的Hilbert濾波器的頻率范圍為40 Hz~960 Hz,，所以驗證時將用頻率為150 Hz正弦波信號通過所設計的濾波器,，觀察結(jié)果來驗證該濾波器是否實現(xiàn)了π/2移相。
    本文討論了無功功率與有功功率之間的關(guān)系,，以及計算無功功率方法中移相法的兩種方法,，根據(jù)在Matlab中對基于采樣點平移的移相法和Hilbert濾波器法的仿真可以看出，基于采樣點平移的移相法在實際應用中有局限性,，只能在一些要求不高的場合采用,。而Hilbert濾波器法可以做到移相準確、計量精度高,，因此,，基于 Hilbert變換的移相算法是無功計量中較好的方法。
參考文獻
[1] 王薇,，王曉茹,，黃曉青.無功功率測量的Hilbert數(shù)字濾波器研究[J].電測與儀表，2007,，44(3):9-12.
[2] 吳思聰,，趙威威，陳燕紅.Hilbert變換在無功電能計量中的應用研究[J].電測與儀表,，2009,，46(6):35-38.
[3] 陳國通.無功功率和電能的移相算法[J].電力學報,， 2007，22(4):228-231.
[4] 陳嘯晴,，粟梅.幾種無功功率測量算法的仿真比較[J].廣東技術(shù)師范學院學報，2008(12)：25-28.
[5] 楊曉潔.基于SOPC技術(shù)的三相電能計量算法研究[D].北京:首都師范大學,，2008.