隨著社會發(fā)展,，快速有效的自動身份驗證應(yīng)用廣泛,。生物特征是人類的內(nèi)在屬性，具有很強的自身穩(wěn)定性和個體差異性,，所以它是身份驗證最理想的依據(jù),。其中，人臉相比其他的人體生物特征具有直接,、方便,、友好等特點，所以利用人臉特征進行身份驗證是最自然直接的手段,，并易于為用戶所接受,。性別鑒別作為其中特殊的一部分，可以加強人機交互系統(tǒng)的靈活性,，而且可以對特殊環(huán)境下與性別相關(guān)的地方出入進行限制,，收集有價值的統(tǒng)計信息(如每天出入的男性、女性數(shù)量,，對酒吧,、商場、零售業(yè)提供有價值的服務(wù))等,。
1 性別分類算法
性別分類是一個典型的二類問題,，一般方法是通過輸入一副人臉圖像X，通過預(yù)處理,，特征提取,，分類器等過程后來決定X的類別。這里的性別分類算法如圖1所示,，它是由預(yù)處理,、特征提取、分類器3個部分組成,。
其中預(yù)處理主要是幾何變換和區(qū)域直方圖處理。通過這些工作保障了人臉幾何(方向,，大小)的不變性,。基本消除了背景的影響和部分光照影響,，提高了識別的精度,。然后再預(yù)處理的基礎(chǔ)上進行主元分析提取特征,，獲得主元分析PAC(Principal components Analysis)主元子空間和線性鑒別分析LDA(Linear Discriminant Analysis)特征子空間，最后利用分離器(人臉樣本訓(xùn)練獲得)進行分類,。
1．1 預(yù)處理
該性別分類算法主要采用，幾何處理+整體直方圖處理(HG),，幾何處理+區(qū)域直方圖處理(RHG)2種方法進行預(yù)處理，并進行比較,。
1．1．1 幾何處理
1)圖像的縮放
MATLAB圖像處理工具箱中的函數(shù)imresize可對圖像進行縮放操作,，常用的格式為：
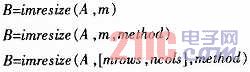
B是縮放后圖片,；A是原始圖片,；m表示縮放倍數(shù)(m>1時圖片放大；m<1時圖片縮小),；method是縮放的插值方法(默認(rèn)為最近鄰插值法),；[mrows,，ncols]指輸出圖片大小為mrowsxncols,。
2)圖像的旋轉(zhuǎn)處理
有些待分類的圖像，人臉是歪斜的,，這時要對圖像進行旋轉(zhuǎn)處理如圖2所示,。但旋轉(zhuǎn)時各像素的坐標(biāo)會發(fā)生變化，使得旋轉(zhuǎn)之后不能正好落在整數(shù)坐標(biāo)處,，需要進行插值，工具箱中函數(shù)imrotate方法可以對圖像進行插值旋轉(zhuǎn)(默認(rèn)方法是最近鄰插值法),。常用的語法格式為：
其方法中對應(yīng)的參數(shù)意義為：angle為圖像A按照逆時針旋轉(zhuǎn)的角度,，method是選擇的插值方法。
3)圖像的剪切
當(dāng)只需要圖像中的一部分時,，如實驗中只需要人臉圖片,，就要對圖像進行剪切處理，在MATLAB圖像處理工具箱中提供函數(shù)imcrop用于剪切圖像中的一個矩形子圖,，用戶可以根據(jù)這個矩形頂點的坐標(biāo),，也可以用鼠標(biāo)指針選取這個矩形。該函數(shù)常用的格式如下：
其中前3種格式為交互式地對灰度圖像,、索引色圖像和真彩色圖像進行剪切。后3種方式是按指定的矩形框rect剪切圖像,，rect是一個四元向量[xmin,，ymin width heigth],，分別表示矩形的左上角坐標(biāo)、寬度和高度,。
1．1. 2 整體直方圖處理(HG)
直方圖方法是建立在概率論的基礎(chǔ)上,，是通過改變直方圖的形狀來達到增強圖像對比度的效果。常用的方法有直方圖均衡化和直方圖規(guī)定化,。直方圖均衡化又稱直方圖平坦化,，是將一已知灰度概率密度分布的圖像，經(jīng)過某種變換成一幅具有均勻灰度概率密度分布的新圖像,，其結(jié)果是擴展了像元取值的動態(tài)范圍,，從而達到增強整體對比度的目的。采用MATLAB工具箱中histeq方法對圖像進行直方圖處理,。
常用B=histeq(A),。
1．1．3 區(qū)域直方圖處理(RHG)
直方圖處理是探討了亮度標(biāo)準(zhǔn)化方法的一般計算模型，為了解決偏光問題,，又提出了亮度標(biāo)準(zhǔn)化的分塊策略,，采用將圖片等分4份，對偏光嚴(yán)重的人臉圖片進行區(qū)域直方圖處理后再合成原始大小圖片,。針對圖像整體直方圖和分塊區(qū)域化后直方圖取得的效果進行比較,，如圖3所示。
1．2 PCA算法的基本原理
主成分分析法PCA(Principal Component Analysis)其目的是在數(shù)據(jù)空間中找到一組向量以盡可能地解釋數(shù)據(jù)的方差,，從而用降維后的低維向量保存原數(shù)據(jù)中的主要信息,，使數(shù)據(jù)更易于處理。主要原理就是基于對原始數(shù)據(jù)進行統(tǒng)計分析,，利用線性變換,，對高維數(shù)據(jù)進行分析與壓縮。由于人臉結(jié)構(gòu)的相似性,，當(dāng)把人臉圖像樣本進行規(guī)一化并抽成一個高維向量后,，這些圖像在高維空間中不是隨機或散亂地分布的，
而是存在某種規(guī)律,。通過主元變換進行人臉識別的方法被稱為“特征臉”方法,。
主成分分析是將分散在一組變量上的信息集中到某幾個綜合指標(biāo)(主成分)上的探索性統(tǒng)計分析方法，以便利用主成分描述數(shù)據(jù)集的內(nèi)部結(jié)構(gòu),，實際上起著數(shù)據(jù)降維的作用,。
假設(shè)有一幅大小為N1xN2的灰度圖像P(x，y),，其中x∈[1,，N1]，y∈[1，N2],，且像素值P(x,，y)滿足P(x，y)∈[0,，1],，x為行索引值，y為列索引值,。為了應(yīng)用PCA技術(shù),，首先要將該人臉從二維矩陣轉(zhuǎn)化為一維向量，這可以通過如下操作達到要求,。
將kxl的矩陣C的第1行轉(zhuǎn)置,，然后將C的第2行轉(zhuǎn)置拼接于其后，如此類推,，直到最后將第k行轉(zhuǎn)置并拼接起來,。例如，矩陣
在經(jīng)過上述操作以后,，就變?yōu)?a11 a12 a13 a21 a22 a23)T,。一幅大小為N1xN2的灰度圖像可以被轉(zhuǎn)換為N1xN2維的向量，因此可以將一幅人臉圖像視為高維空間中的一個點,，并用PCA技術(shù)使用少數(shù)特征來近似描述人臉圖像在高維空間中的分布,。
考慮n(N1xN2)維空間中的m個向量x1，x2,，…,，xm為了降低維數(shù)，需要用一個m維的向量x’來近似模擬,，其中m<
通常假設(shè)隨機向量(x-μ)為零均值,，即μ取值為隨機向量x的期望
WT=(w1,，w2，…,，wm)為一個mxn的變換矩陣。(x-μ)是一個(nxl)n維的向量,。y是m維的向量,。這是一個線性的變換，式(1)是個內(nèi)積,，引述內(nèi)積的定義：
圖4為式(3)的物理意義,。
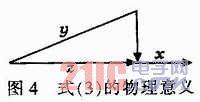
如果使式(3)具有投影的意義，即z向量是y向量到x向量的方向上的投影,，如圖4所示,，那么必須使得|x|=1,，即z=|y|cosθ。
現(xiàn)在考慮PCA變換矩陣W第一個向量
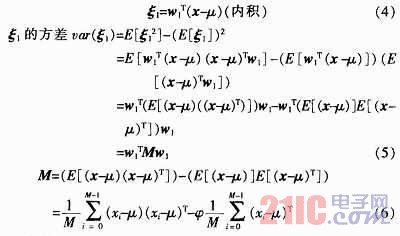
如果在條件|w1|=1使ξ1的方差達到最大,，希望最大程度的保持樣本集x原有的差異(Variance),。也就是要
的值最大。這成為了一個優(yōu)化問題,。目標(biāo)函數(shù)是
,，條件是
，使用拉格朗日乘數(shù)法
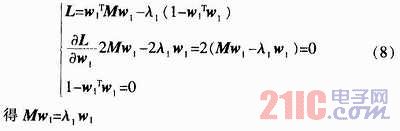
因此λ1是協(xié)方差矩陣M的一個特征值,，w1是λ1對應(yīng)的特征向量,。要使其方差最大，就必須使
的值最大,，因為
,，所以，λ1應(yīng)是M矩陣的最大特征值,。
現(xiàn)在考慮PCA變換矩陣WT第2到第m個向量
,，這里的向量是互不相關(guān)的，代表著不同的投影方向,，這樣可以提取出不同的主特征,。要滿足這個條件，考慮協(xié)方差矩陣M,，它是對稱的陣,，有多個特征值λi，i∈(1,，n),，因此，轉(zhuǎn)換矩陣中w1,，w2,，…，wm應(yīng)該如下取值：首先求出M的特征向量和對應(yīng)的特征值,，然后依據(jù)特征值排序為λ1≥λ2≥…≥λn,，它們對應(yīng)的特征向量分別為w1，w2,，…,，wn，則取最前面的m個向量w1,，w2,，…，wm組成PCA變換矩陣。
出于數(shù)值計算方面的考慮,，通常不使用M矩陣求特征值,，和特征值對應(yīng)的特征向量，而使用奇異值分解(SVD,，Singular Value Decompo-sition)來計算前m個主方向,。
1．3 SVD奇異值分解定理
SVD定理：設(shè)A是秩為r的nxr維的矩陣，則存在兩個正交矩陣：
由于M=AAT,，其中,，故構(gòu)造矩陣
，M為訓(xùn)練樣本集中的樣本個數(shù),。容易求出其特征值λi及其相應(yīng)的特征向量vi(i=O,，1，…,，M-1),。由推論式可知，M的特征向量ui
1．4 LDA方法算法說明
LDA(Linear Discriminant Analysis)方法也稱為線性判別分析方法,。它選擇與類內(nèi)散布的正交的矢量作為特征臉空間,，從而能夠壓制圖像之間的與識別信息無關(guān)的差異，對光照及人臉表情變化都不太敏感,。這種方法的最終目的就是找到一些特征使得類間離散度和類內(nèi)離散度的比值最大,。
式中，Pi是先驗概率,，mi是Ci類的均值,，m是所有樣本的均值。
如果Sw是非奇異矩陣,，在投影以后,，各類樣本之間盡可能的分開一些，即類間離散度越大越好,，同時各類樣本的內(nèi)部盡量密集起來,，即類內(nèi)離散度越小越好。因此可以定義Fisher準(zhǔn)則函數(shù)如下：
如果Sw非奇異,，就是求Sw-1Sb的特征值及其特征向量問題,。其中該矩陣最多只有C-1個非零特征值，C是類別數(shù)目,。
1．5 PCA-LDA算法的融合
將PCA算法與LDA算法構(gòu)造的特征子空間進行融合,，獲得其融合空間，然后,，將訓(xùn)練樣本與測試樣本分別朝該融合特征空間投影,，獲得識別特征，最后,，利用最近鄰準(zhǔn)則完成性別鑒定,。
PCA-LDA算法融合是根據(jù)PCA算法和LDA算法的特征子空間W1，W2進行融合,，即：W1=W1*W2,，得到融合特征空間：Ws。其中
,，其中行數(shù)表示訓(xùn)練樣本維數(shù),，列表示LDA算法降維后的特征向量個數(shù)。在訓(xùn)練過程中,，將訓(xùn)練樣本矩陣X投影到融合特征空間Ws中,，使得每一個向量代表一個訓(xùn)練樣本的特征，在測試過程中,，首先將測試樣本規(guī)范化,，即將測試樣本減去平均值，在轉(zhuǎn)化成列向量向PCA空間和融合空間投影獲得識別特征,，最后將測試樣本的識別特征和訓(xùn)練樣本的識別特征進行一一比較,，依據(jù)鄰近準(zhǔn)則得到最小距離d所屬樣本的屬性。
2 試驗步驟與過程
2．1 試驗步驟
2．1．1 樣本的訓(xùn)練
1)照片的預(yù)處理,，照片歸一化,；
2)求得訓(xùn)練樣本的平均臉、零均值,；
3)提取訓(xùn)練樣本的PCA矩陣,；
4)提取訓(xùn)練樣本的LDA矩陣；
5)PCA矩陣和LDA矩陣融合獲得分類器,。
2．1．2 待測試照片的識別
1)將測試照片預(yù)處理,；
2)測試照片向融合空間投影，得到低微空間上的點,；
3)計算該點與訓(xùn)練樣本的“特征臉”距離比較,，輸出距離最近的那張“特征臉”的信息，從而達到性別識別目的,。
2．2 實驗過程
本實驗中所用到的圖片來源于ORL人臉圖像庫和yale人臉圖像庫,，ORL人臉圖像庫是英國劍橋大學(xué)從1992到1994年間在實驗室采集到的人臉圖像數(shù)據(jù)，由40人,，每人10幅,，共400幅照片，每幅分辨率為92xll2,，主要包括拍攝時間,、光照條件,、人臉表情和面部遮掩物的不同。而yale人臉圖像庫是耶魯大學(xué)提供的,，共有15人,，每人11張照片，分辨率為100x100,，主要包括光照條件的變化表情的變化等,。
該試驗采用yale圖像庫中的人臉照片。利用平均臉公式,，實驗中所得到的平均臉如圖5和圖6所示,。
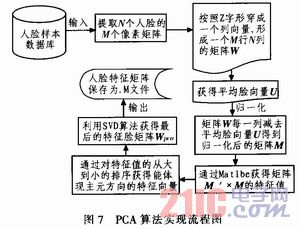
PCA矩陣提取試驗分析，圖7為PCA算法實現(xiàn)流程圖,。
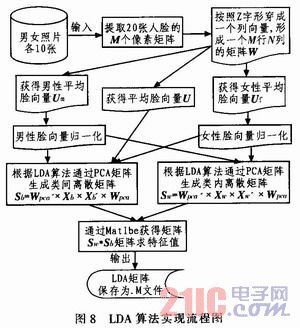
LDA矩陣提取試驗分析,，圖8為LDA算法實現(xiàn)流程圖。
然后再將LDA-PCA矩陣融合,；利用歐式距離求出待識別人臉的特征臉再根據(jù)臨近原則實現(xiàn)性別識別,；采用直方圖處理的識別實驗(PCA+L-DA)；采用整體直方圖處理的識別實驗(HG+PCA+LDA),；采用直方圖區(qū)域預(yù)處理的識別實驗(RHG+PCA+LDA),。
3 實驗結(jié)果分析與結(jié)論
實驗結(jié)果如圖9所示，表明：用PCA-LDA融合空間算法的識別正確率都在80％以上,，是比較高的,。采用直方圖處理的識別實驗(PCA+LDA)在3種方法的識別正確率比較中相對較低，且波動性較大,，特別的,，在樣本數(shù)量為20，40時,，出現(xiàn)了0．83,，0．84的正確率，為整個曲線中的低谷,，整體效果相對來說一般,。采用整體直方圖處理的識別實驗(HG+PCA+LDA)正確率曲線相對來說較為平滑，隨著樣本數(shù)量的增加,，整個曲線呈現(xiàn)遞增趨勢,，但識別正確率不是特別理想。采用區(qū)域直方圖預(yù)處理的識別實驗(RHG+PCA+LDA)的正確率整體來說最高,，整個曲線完全凌駕于前2種算法之上,，雖然在小樣本數(shù)量空間內(nèi)出現(xiàn)波動，但波動為曲線的相對波峰,，即識別正確率是提高的,。3種方法在整個樣本空間內(nèi)均為隨著樣本數(shù)量的增加,，識別正確率平穩(wěn)上升，漸趨于完全正確,。但采用區(qū)域直方圖預(yù)處理的識別實驗(RHG+PCA+LDA)后整體識別正確率最高,，為三個算法中在整個樣本空間內(nèi)的相對最優(yōu)算法。
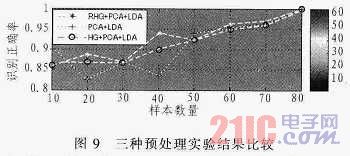
經(jīng)過以上實驗結(jié)果分析,，在進行人臉性別識別時，建議用PCA-LDA融合空間算法,，采用區(qū)域直方圖預(yù)處理(RHG+PCA+LDA),，這樣會達到理想的效果，并且樣本數(shù)量應(yīng)該盡量的多,。