摘 要： 以驅(qū)動(dòng)參量法作為同步實(shí)現(xiàn)模型,，提出一種新的數(shù)字混沌通信方案，并對(duì)傳統(tǒng)混沌加密方法進(jìn)行了改進(jìn)。將公鑰" title="公鑰">公鑰與用于編碼的私鑰分離, 攻擊者只能得到公鑰,，只有權(quán)威的接收者才能得到私鑰,。針對(duì)此方案設(shè)計(jì)了基于ARM處理器的數(shù)字混沌通信編解碼模塊，試驗(yàn)結(jié)果證明該方案具有較好的實(shí)際意義和應(yīng)用價(jià)值。
關(guān)鍵詞： 數(shù)字混沌 混沌編碼 混沌通信 ARM處理器
隨著混沌同步" title="混沌同步">混沌同步手段的不斷發(fā)展,，近些年來(lái)，利用混沌同步思想進(jìn)行保密通信" title="保密通信">保密通信已成為研究熱點(diǎn)[1～2],。筆者對(duì)基于連續(xù)流混沌的模擬通信系統(tǒng)進(jìn)行了研究,，但結(jié)果并不滿意?；煦缤浇庹{(diào)對(duì)模擬器件及電路設(shè)計(jì)要求很高,，理想的通信狀態(tài)難以實(shí)現(xiàn)；其次,，同步信號(hào)的傳輸占用了較多的信道資源,，且易受攻擊，降低了保密性[3～4],。目前,，離散混沌動(dòng)力系統(tǒng)用于保密通信，受到了人們的廣泛重視,。數(shù)字混沌通信系統(tǒng)具有較高的保密性,，加密方法十分靈活；同步信號(hào)與密文信號(hào)可復(fù)用為單信道,，節(jié)省了信道資源,。特別是DSP處理器及ARM核芯片在通信設(shè)備中的使用，為數(shù)字保密通信提供了強(qiáng)大的硬件支持,，從而使加密算法的設(shè)計(jì)更加模塊化,、平臺(tái)化。
本文提出一種多級(jí)數(shù)字混沌保密通信方案,，以驅(qū)動(dòng)參量法[5] 作為同步實(shí)現(xiàn)模型,，并進(jìn)行了改進(jìn)。將公鑰與用于編碼的私鑰分離,；攻擊者只能得到公鑰,，只有權(quán)威的接收者才能得到私鑰。仿真結(jié)果表明,，系統(tǒng)具有較好的安全性和穩(wěn)定性。最后,，筆者設(shè)計(jì)了基于ARM處理器的多級(jí)數(shù)字混沌通信編解碼模塊,，效果理想，其通信速率和通信質(zhì)量基本達(dá)到數(shù)字通信系統(tǒng)的要求,。
1 驅(qū)動(dòng)參量同步
近年來(lái),，人們提出了許多同步方法，其共同點(diǎn)在于系統(tǒng)之間必須存在耦合作用驅(qū)使它們朝相同的狀態(tài)發(fā)展,，最終具有相同的動(dòng)力學(xué)行為,，達(dá)到同步,。
已知qn是一個(gè)離散混沌序列" title="混沌序列">混沌序列，進(jìn)行下面的變換：
其中y=(y1,…,，yn)為非線性系統(tǒng)的狀態(tài)變量,。在驅(qū)動(dòng)作用下，非線性系統(tǒng)原有的狀態(tài)發(fā)生改變,，進(jìn)入一種更加復(fù)雜的混沌態(tài),。
隨著驅(qū)動(dòng)系數(shù)k的增大，參量ξj的變化范圍增大,；當(dāng)k超出某一閾值時(shí),，即參數(shù)ξj的變化范圍足夠大時(shí)，在一個(gè)ξj的共同驅(qū)動(dòng)下,，兩個(gè)或多個(gè)混沌系統(tǒng)會(huì)在新的動(dòng)力學(xué)的基礎(chǔ)上達(dá)到完全同步,。
2 混沌編解碼器的設(shè)計(jì)
圖1為較常見(jiàn)的混沌序列編解碼通信系統(tǒng)框圖?？梢钥吹?，這種通信方式必須在接收端產(chǎn)生與發(fā)射端時(shí)間上同步的混沌同步信號(hào)。而同步信號(hào)的產(chǎn)生需要另加信道,，或者將發(fā)送端的混沌信號(hào)" title="混沌信號(hào)">混沌信號(hào)和已調(diào)混沌序列以復(fù)用的方式發(fā)送,。這些方法雖然解決了收、發(fā)端的同步問(wèn)題,，但是系統(tǒng)的保密性將大打折扣,，用于解碼的混沌序列直接暴露在信道中，一旦被截獲,，破譯的幾率會(huì)相當(dāng)高,。
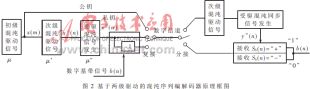
本文采用驅(qū)動(dòng)參量法使接收端與發(fā)送端混沌序列同步，為了進(jìn)一步提高系統(tǒng)的保密性,，在系統(tǒng)中加入了兩級(jí)驅(qū)動(dòng)機(jī)制,。初級(jí)混沌信號(hào)用以驅(qū)動(dòng)次級(jí)混沌，次級(jí)混沌將驅(qū)動(dòng)受驅(qū)混沌信號(hào),，初級(jí)產(chǎn)生的驅(qū)動(dòng)信號(hào)與已編碼信號(hào)以時(shí)分復(fù)用的方式發(fā)送,。在此方式下，在信道中傳輸?shù)牟⒉皇怯糜诮獯a的混沌同步序列(私鑰),，而是驅(qū)動(dòng)參量(公鑰),；在接收端解調(diào)出初級(jí)驅(qū)動(dòng)信號(hào)，還原出用于解碼的受驅(qū)混沌同步信號(hào),，從而大大提高系統(tǒng)的保密性,。對(duì)于非權(quán)威的接收者，還原這個(gè)加密過(guò)程將非常復(fù)雜。圖2給出了本系統(tǒng)的原理圖,。
以經(jīng)典的Logistic映射作為混沌信號(hào)發(fā)生模型,。Logistic映射：
x(n+1)=μ×x(n)×[1-x(n)] (4)
其中0＜x(n)＜1，0＜μ＜4,。由 Lyapunov指數(shù)定義可知,，當(dāng)3.58＜μ＜4時(shí)，該映射是混沌的,。
具體過(guò)程為：初級(jí)混沌驅(qū)動(dòng)信號(hào)x(m),，以相等的時(shí)間間歇Td改變次級(jí)混沌的初值x′(mTd+1)，在一個(gè)時(shí)間段內(nèi),，時(shí)間間歇Td=
,；次級(jí)混沌驅(qū)動(dòng)信號(hào)x′(n)，以驅(qū)動(dòng)參量法為模型,，驅(qū)動(dòng)收,、發(fā)端受驅(qū)混沌信號(hào)的參量μ′′，使整個(gè)系統(tǒng)達(dá)到同步,，受驅(qū)后產(chǎn)生的混沌同步信號(hào)x′′(n),、y′′(n)將參與編、解碼,。
系統(tǒng)中編碼部分采用鍵控方式,，當(dāng)所發(fā)送基帶信號(hào)為“1”時(shí)，受驅(qū)混沌信號(hào)原樣發(fā)送,；為“0”時(shí),，受驅(qū)混沌信號(hào)取反后發(fā)送。在適當(dāng)?shù)剡x擇系統(tǒng)參數(shù)后,，從首歸映象(如圖3(a)所示)可以看出,，兩級(jí)驅(qū)動(dòng)產(chǎn)生的混沌信號(hào)具有十分復(fù)雜的混沌態(tài)，這也正是此方案用于保密通信的一大優(yōu)勢(shì),。
設(shè)編碼后的密文為Sb(n),，公鑰與密文復(fù)接后的信號(hào)服從表1數(shù)據(jù)格式。
為了驗(yàn)證本方案的可實(shí)現(xiàn)性,，以32位運(yùn)算精度進(jìn)行數(shù)值模擬,，采用定點(diǎn)運(yùn)算方式。對(duì)于Logistic映射,，初級(jí)混沌μ=3.8906,Td=100;次級(jí)混沌μ′=4,；驅(qū)動(dòng)參量初值ξj(0)=4，驅(qū)動(dòng)系數(shù)k=1.8594,；發(fā)送端受驅(qū)混沌初值x′′(0)=0.4375,，接收端初值y′′(0)=0.9625。仿真結(jié)果如圖3(b)所示,，受驅(qū)的兩路混沌演化至850點(diǎn)后達(dá)到同步,。
3 系統(tǒng)硬件實(shí)現(xiàn)
混沌對(duì)初值的敏感性決定了混沌迭代運(yùn)算必須是高精度的，筆者選用PHLIPS的LPC2200系列ARM7微處理器,，構(gòu)建了32位數(shù)字混沌通信試驗(yàn)平臺(tái),。將正弦信號(hào)采樣、量化編碼后作為基帶信號(hào)參與鍵控調(diào)制,，在500kbps的碼元傳輸速率下,，接收端無(wú)失真地解調(diào)出了基帶信號(hào)，且收,、發(fā)端同步性能良好,。圖4是專為本系統(tǒng)設(shè)計(jì)的信道監(jiān)測(cè)軟界面。
試驗(yàn)結(jié)果表明,，此方案對(duì)通信速率的要求并不苛刻,。在32位運(yùn)算精度下，受驅(qū)混沌的同步速度要快于數(shù)值模擬時(shí)的情形,。對(duì)幾組試驗(yàn)結(jié)果分析表明,，混沌同步的演化過(guò)程控制在200點(diǎn)以內(nèi)。
另外,，信道誤碼對(duì)信號(hào)的解調(diào)也是有影響的,。在一幀信息內(nèi)，如果公鑰部分發(fā)生誤碼,，將影響到一幀內(nèi)的所有位信息,，但不會(huì)影響到下一幀；如果密文部分發(fā)生誤碼,，將只影響到發(fā)生誤碼的位信息,，同一幀內(nèi)的其它位信息不會(huì)受到影響。根據(jù)以上分析,，對(duì)于單極性基帶信號(hào),，可得出解碼錯(cuò)誤率PI和信道誤碼率Pe之間的關(guān)系：
其中A為基帶信號(hào)峰值,σn為噪聲均方根值?？梢钥闯?，在(0，1)內(nèi),，隨著Pe的增大PI亦呈逐漸增長(zhǎng)趨勢(shì),。
本文提出了一種多級(jí)數(shù)字混沌保密通信方案，結(jié)合驅(qū)動(dòng)參量同步方法,，著重介紹了系統(tǒng)編解碼器的設(shè)計(jì)與實(shí)現(xiàn),。與常規(guī)混沌保密通信系統(tǒng)相比，此方案的優(yōu)越性在于：
(1)將驅(qū)動(dòng)參量與已調(diào)信號(hào)以數(shù)字復(fù)用方式發(fā)送，使用單信道方式,，降低了系統(tǒng)開(kāi)銷,；
(2)即便竊聽(tīng)者獲取了驅(qū)動(dòng)參量(公鑰)和已調(diào)信號(hào)(密文)，在不知道受驅(qū)機(jī)制的情況下,，根本無(wú)法還原出用于解調(diào)的混沌序列(私鑰),；
(3)驅(qū)動(dòng)參量與已調(diào)信號(hào)復(fù)用，在一幀數(shù)據(jù)中既有密文信息又有用于解密的驅(qū)動(dòng)信號(hào),，從而達(dá)到一種編碼同步,，避免了時(shí)域混沌同步實(shí)現(xiàn)的復(fù)雜性。
在硬件資源允許的情況下,，可以增加混沌驅(qū)動(dòng)的層次性,，提升系統(tǒng)復(fù)雜度，進(jìn)一步提高系統(tǒng)保密性,。
參考文獻(xiàn)
1 Pecora L M, Carroll T L. Synchronization in chaotic system[J].Phys Rev Lett,1990,；64(8):821～824
2 Frey D. Chaotic digital encoding: An approach to secure commuciation[J]. IEEE Transactions on Circuits and Systems-II, 1993; 40(10): 660～666
3 Chua L O. Chua′s circuit: ten years later[J]. IEICE Trans. Fundamentals,1994; E77—A(1):1811～1821
4 Sharma N. Exploring synchronization to combat channel dis-tortions in communication with chaotic system[J]. Int. J.Bifurcation and Chaos,2000;10(4):777～785
5 楊世平，牛海燕,，田 鋼等. 用驅(qū)動(dòng)參量法實(shí)現(xiàn)混沌系統(tǒng)的同步[J]. 物理學(xué)報(bào), 2001,；50(4):619～623
6 Werter M J.An improved chaotic digital encoder[J]. IEEE Transactions on Circuits and Systems-II,1998；45(2):227～229
7 Yang T,Chua L O. Error Performance of chaotic digital codedivision multiple access(CDMA) systems[J].Int J Bifurcation and Chaos,1998,；8(10):2047～2059
8 Kolumban G,Kennedy M P, Chua L O.Role of synchronization in digital communications using chaos-part II:chaotic modu-lation and chaotic synchronization[J]. IEEE Transactions on Circuits and Systems I.1997; 44(14): 1129～1141
9 HASLER M.Synchronization of chaotic systems and transmis-sion of information[J]. Int J Bifurcation and Chaos, 1998;8(3): 639～644