摘 要：遺傳算法是一種模仿自然界生物進(jìn)化過程中選擇和遺傳的機(jī)理而構(gòu)造出的一種優(yōu)化搜索算法,。但是,，簡單遺傳算法的收斂速度較慢、穩(wěn)定性較差,。針對這些同題,，本文提出了幾種方法來改善遺傳算法性能的操作，在文中分別討論了該操作的思路,，實(shí)現(xiàn)的方法,。并給出了它在工業(yè)控制中的應(yīng)用。
關(guān)鍵字：工業(yè)控制 遺傳算法 交叉 遺傳操作
1. 前言
　　優(yōu)化算法和程序是是當(dāng)今計(jì)算機(jī)時代科學(xué)和工程問題研究中最重要的工具之一,。一個好的優(yōu)化算法應(yīng)具備兩個基本特征（設(shè)以求全局最大主峰為例）：一是要找到主峰而不是眾多的次峰;二是爬峰速度要快,。此外，它還應(yīng)具有通用性,，最好能用于“黑箱”問題的尋優(yōu),。。如能有一種優(yōu)化算法既可保留上述兩種基本算法的簡單和通用特征,，而又有高的尋優(yōu)準(zhǔn)確度和效率,，顯然是人們夢寐以求的。遺傳算法（GA）為此開辟了一條誘人的道路,。
　　遺傳算法是由美國密執(zhí)安大學(xué)Holland等人,，經(jīng)過20余年的努力而發(fā)展起來的，它將描述自然界生物進(jìn)化的達(dá)爾文學(xué)說“物盡天擇,，適者生存”的原理引入到算法中,。特別是近十年，由于計(jì)算機(jī)性能的提高,，以及并行分布式計(jì)算的推廣,，遺傳算法由于自身獨(dú)特的優(yōu)勢而越來越受到人們的重視。進(jìn)入21世紀(jì),，遺傳算法已成為國際上的一個研究熱點(diǎn),，圍繞遺傳算法，有一大批學(xué)者在從事下列方面的研究：遺傳算法的機(jī)理,、算法的收斂性和復(fù)雜度,、編碼方法,、選擇方法、雜交和變異方法,、遺傳的操作方式等,。到目前為止，對各種問題的研究尚未有定論,，正由于許多問題的存在激勵著人們進(jìn)行不斷的探索和研究,。
2. 簡單遺傳算法簡介
　　簡單遺傳算法的基本思想是把待優(yōu)化問題的參數(shù)編碼成二進(jìn)制位串的形式，然后由若干個位串形成一個初始種群作為待求問題的候選解,，經(jīng)過選擇,、交叉,、變異的迭代搜索過程,，最終收斂于最優(yōu)狀態(tài)。
　　算法過程如下：
　　步驟1：初始化,，隨機(jī)產(chǎn)生一個規(guī)模為P的初始種群,，其中每個個體為二進(jìn)制位串的形式，也就是染色體,，每個二進(jìn)制為稱為基因,。
　　步驟2：計(jì)算適應(yīng)度，計(jì)算種群中每個個體的適應(yīng)度,。
　　步驟3：選擇,，選擇是指從群體中選擇優(yōu)良的個體并淘汰劣質(zhì)個體的操作。它建立在適應(yīng)函數(shù)評估的基礎(chǔ)上,。適應(yīng)度越大的個體,，被選擇的可能性就越大，它的下一代的個數(shù)就越多,。選擇出來的個體放入配對庫中,。
　　步驟4：交叉，從種群中隨機(jī)選擇兩個染色體,，按一定的交叉概率進(jìn)行基因交換,，交換位置的選取也可以是隨機(jī)的。
　　步驟5：變異,，從種群中隨機(jī)選擇一個染色體,，按一定的變異概率進(jìn)行基因變異。
　　步驟6：若發(fā)現(xiàn)最優(yōu)解或者到達(dá)迭代次數(shù),，則算法停止,。否則，轉(zhuǎn)步驟2,。
3. 提高遺傳算法收斂速度的策略
　　初始種群的選擇
　　初始種群的優(yōu)劣對算法的效率和結(jié)果都有重要的影響,，要搜索全局最優(yōu)解,，初始種群不僅要規(guī)模相當(dāng)而且應(yīng)該在解空間均勻分布?；具z傳算法是按照隨機(jī)方法在最優(yōu)解分布范圍內(nèi)產(chǎn)生一定數(shù)目的個體組成初始種群,。
　　本文按照一定的模式選擇種群。將種群分成幾類,。例如,，如果我們選擇初始種群為100個，那么將種群按照不同的模式均勻分成10類,。每個類中的染色體有相同的模式,。由下面的操作可知，這樣做能夠保證了群體的多樣性,。
　　適應(yīng)度比例法的改進(jìn)
　　在遺傳算法的運(yùn)行過程中,，每一代都會產(chǎn)生一些優(yōu)良個體。如果按照傳統(tǒng)的選擇方法,，它們的優(yōu)良模式有可能被后面的遺傳操作破壞,，就會降低群體的平均適應(yīng)度，這樣對進(jìn)化是不好的,。所以我們改進(jìn)的目標(biāo)是保證最優(yōu)解的生存,。最優(yōu)個體（這里的最優(yōu)個體來自全體染色體的10%）不按比例進(jìn)行復(fù)制，直接保留到下一代中,。因?yàn)閺?fù)制的結(jié)果容易使遺傳算法陷入局部最優(yōu)解,。導(dǎo)致各個個體間的適應(yīng)度趨于一致。
　　具體操作過程為：
　?。?）找出每個模式中適應(yīng)度最高的個體,。該個體不進(jìn)行交叉和變異。
　?。?）對同一模式中其它個體進(jìn)行遺傳操作,。即交叉和變異是在同一個模式中的不同個體（最優(yōu)的除外）之間進(jìn)行。
　?。?）在每個模式中,，經(jīng)過交叉和變異后的每個個體進(jìn)行適應(yīng)度比較。依然保留最優(yōu)的個體,。
　　最優(yōu)保存策略是選擇操作的一部分,，它能夠保證不能破壞優(yōu)良模式。也是遺傳算法收斂性的一個重要保證條件,。該策略與下面敘述的交叉和變異操作結(jié)合在一起,，能夠得到良好的效果。
　　交叉方式的改進(jìn)
　　交叉是指把兩個父代個體的部分結(jié)構(gòu)加以替換重組而生成新個體的操作,。交叉的目的是為了能夠在下一代產(chǎn)生新的個體,。通過交叉操作,，遺傳算法的搜索能力得以飛躍性的提高。交叉是遺傳算法獲取新優(yōu)良個體的最重要手段,。
　　交叉的概率一般選擇的都很大,。本文的交叉概率是根據(jù)交叉結(jié)果來決定的。無論是選擇單點(diǎn)交叉還是多點(diǎn)交叉或者其它交叉方式,，改進(jìn)的目標(biāo)是保證子代的適應(yīng)度大于父代,。我們選用的交叉方法是：所有個體（除去最優(yōu)的10%）中每兩個組成一對，全部進(jìn)行交叉,。根據(jù)交叉結(jié)果選擇此次交叉是否進(jìn)行,。如果一對染色體，我們假設(shè)為A和B,，再假設(shè)交叉的結(jié)果為A1和B1,，那么會出現(xiàn)四種情況，（1）A1>A,，B1>B;（2）A1B;（3）A1>A,，B1
　　變異方式的改進(jìn)
　　變異就是以很小的概率（即變異率）隨機(jī)地改變?nèi)后w中個體（染色體）的某些基因的值,。變異操作的基本過程是：對于交叉操作中產(chǎn)生的后代個體的每一基因值,，產(chǎn)生一個[0，1]之間的偽隨機(jī)數(shù),，如果這個偽隨機(jī)數(shù)小于變異概率,，就進(jìn)行變異操作。在二進(jìn)制編碼方式中,，變異算子隨機(jī)地將某個基因值取反,，即0變成1，或1變?yōu)?,。變異本身是一種局部隨機(jī)搜索,，與選擇、交叉算子結(jié)合在一起,，就能避免由于選擇和交叉算子而引起的某些信息的永久性丟失,。保證了遺傳算法的有效性，使遺傳算法具有局部的隨機(jī)搜索能力,。同時使得遺傳算法保持群體的多樣性,，以防止出現(xiàn)未成熟收斂。在變異操作中,，變異率不能取的太大,，如果大于0.5，遺傳算法就退化為隨機(jī)搜索,，而遺傳算法的一些重要的數(shù)學(xué)特性和搜索能力也就不復(fù)存在了,。
　　本文使用的變異概率是根據(jù)是由交叉方式的結(jié)果決定的,。在交叉方式中，每個模式都可能出現(xiàn)不良個體,，如果不良個體數(shù)量大于50%,，那么說明此模式不良，應(yīng)該進(jìn)行淘汰,。我們采用的方法是對此模式進(jìn)行變異,。引進(jìn)新的模式。如果不良個體數(shù)量小于50%,，那么就對這些不良個體進(jìn)行變異,。在不影響模式的前提下，進(jìn)行變異,。即在每個染色體的基因上,，隨機(jī)的選擇一位，使之變異,。至此,，新的一代產(chǎn)生了。
4. 算法過程
　　算法的流程圖如圖1,。

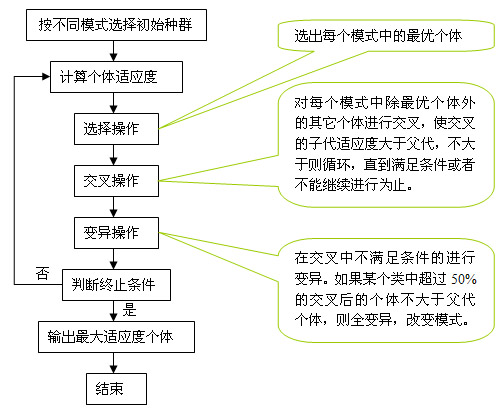
圖1 改進(jìn)的遺傳算法程序框圖
5. 在工業(yè)控制中的應(yīng)用
　　遺傳算法應(yīng)用與工業(yè)控制可以做到以下幾個方面：
　?。?）控制過程的監(jiān)控;在工業(yè)控制監(jiān)控過程中，有些系統(tǒng)會產(chǎn)生大量的隨機(jī)的數(shù)據(jù)和不確定的因素,，因此精確建模比較困難,。也是因?yàn)閿?shù)據(jù)的隨機(jī)性和不確定性因素，造成工業(yè)監(jiān)控系統(tǒng)難以準(zhǔn)確控制,。利用遺傳算法進(jìn)行過程監(jiān)控,，首先建立控制系統(tǒng)的理論控制模型，然后利用遺傳算法能在大量數(shù)據(jù)上的尋優(yōu)優(yōu)勢,，提供監(jiān)控方案,。并且遺傳算法也能進(jìn)行自適應(yīng)控制來隨時調(diào)整控制模型，達(dá)到監(jiān)控的優(yōu)化并且使系統(tǒng)更趨于穩(wěn)定,。
　?。?）控制過程故障診斷（提供決策方案）;把遺傳算法理論與技術(shù)應(yīng)用于控制過程故障診斷能夠模擬專家系統(tǒng)實(shí)現(xiàn)對控制器的故障檢查。故障檢測過程中的參數(shù)一般都具有非線性特征,，如果使用確定性的方法,，很難建立其數(shù)學(xué)模型。遺傳算法應(yīng)用在智能診斷中,，可以解決多變量非線性系統(tǒng)問題,。而且系統(tǒng)的魯棒性好，對參數(shù)變化不敏感，并且可以做出決策供維護(hù)人員參考,。
　?。?）系統(tǒng)參數(shù)辯識（參數(shù)優(yōu)化）;隨著工業(yè)控制規(guī)模的不斷加大和時間的不斷積累，需要保存和后期處理的數(shù)據(jù)越來越龐大,，這就對工業(yè)控制系統(tǒng)提出了更高的要求,。大量的參數(shù)構(gòu)成了整個工業(yè)控制過程，原來的工業(yè)控制系統(tǒng)實(shí)時處理數(shù)據(jù)的能力很強(qiáng),，但是后期數(shù)據(jù)的處理能力顯得有些力不從心,，遺傳算法在大量數(shù)據(jù)的處理方面擁有較多優(yōu)勢，在參數(shù)優(yōu)化方面也有著其他算法不可比擬的優(yōu)越性,，如PID參數(shù)控制等,。所以自從90年代以來在我國的工業(yè)控制系統(tǒng)中的應(yīng)用也越來越廣泛。遺傳算法和工業(yè)控制系統(tǒng)的結(jié)合,，不僅使當(dāng)今的自動化更具靈活性,、完整性、經(jīng)濟(jì)性和安全性,，而且為信息集成和自動化系統(tǒng)提供了新的結(jié)構(gòu),，具有良好的發(fā)展前景。
　?。?）控制器的優(yōu)化設(shè)計(jì),。遺傳算法在很多領(lǐng)域得到了較好的應(yīng)用，運(yùn)用遺傳算法設(shè)計(jì)的控制器實(shí)時性好,、響應(yīng)快,并具有自適應(yīng)調(diào)節(jié)功能,且精確,、控制平穩(wěn),能滿足較高要求,具有較高性價比,。
6. 結(jié)論
　　本論文的創(chuàng)新點(diǎn)在于針對工業(yè)控制中經(jīng)常使用的控制方式方法,，使用我們改進(jìn)的遺傳算法，使得它能在工業(yè)控制中更好的使用,。系統(tǒng)的運(yùn)行結(jié)果跟程序本身有關(guān)也跟機(jī)器的性能有關(guān),。視情況不同而不同。對于不同的控制函數(shù)模型本文的遺傳算法并不是十分優(yōu)秀,。但是對于某些控制模型來講,，還是有一些優(yōu)勢。在控制系統(tǒng)常用的非線性函數(shù)的情況下,，本文的算法比標(biāo)準(zhǔn)的遺傳算法有更好的結(jié)果,。在實(shí)驗(yàn)階段處理簡單的函數(shù)的問題上，也具有相當(dāng)?shù)膬?yōu)勢,。
　　到目前為止,，還沒有找到一種能適合所有類型函數(shù)的遺傳算法。目前對遺傳算法的改進(jìn)大多數(shù)集中在選擇、交叉,、變異,、適應(yīng)度等的參數(shù)選擇上，而這些改進(jìn)也沒有統(tǒng)一的形式,。本文的算法在交叉問題處理上,，看上去似乎煩瑣些，實(shí)驗(yàn)結(jié)果表明,，它可以減少遺傳的迭代次數(shù),。這種改進(jìn)只適合某些特定的函數(shù)。所以對遺傳算法的研究和改進(jìn)還需要做大量的工作,。
參考文獻(xiàn)
　　[1] 司徒浩臻等.基于遺傳算法的多序列比對算法研究.微計(jì)算機(jī)信息,，2006，6-2：22
　　[2] A.H.Wright.Genetic algorithms for real parameter optimization, Amer: Sci, 1991
　　[3] K. Deb and H.-G. Beyer, Self-adaptation in real-parameter genetic algorithms with simulated binary Crossover, Proc. of the genetic and Evolutionary Computation, 1999.
　　[4] Chiba, T, Okado, S, Fujii, I, and Itami, K. （1996b）. “Optimum support arrangement of piping systems using genetic algorithm.” J. Pressure Vessel Techno. 118, 507–512.
　　[5] Nolle, L., Armstrong, D.A., Hopwood, A.A. and Ware, J.A., \Simulated Annealing and Genetic Algorithms Applied to Finishing Mill Optimization for Hot Rolling of Wide Steel Strip", International of Knowledge-Based Intelligent Engineering System, 6, 2, 104-111, 2002.