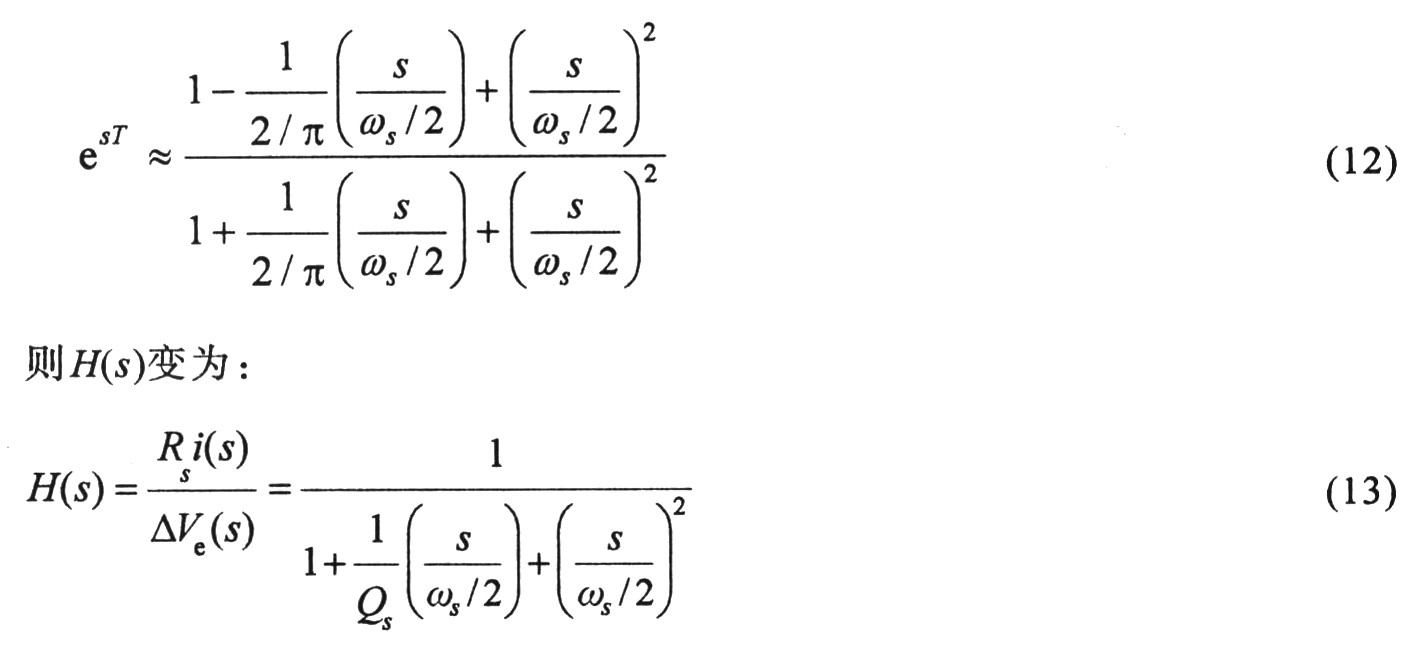DC-DC開關電源因體積小,重量輕,,效率高,,性能穩(wěn)定等優(yōu)點在電子、電器設備,,家電領域得到了廣泛應用,,進入了快速發(fā)展期。DC-DC開關電源采用功率半導體作為開關,,通過控制開關的占空比" title="占空比">占空比調整輸出電壓,。其控制電路拓撲分為電流模式和電壓模式,電流模式控制因動態(tài)反應快,、補償電路簡化,、增益帶寬大、輸出電感小和易于均流等優(yōu)點而被廣泛應用,。電流模式控制又分為峰值電流" title="峰值電流">峰值電流控制和平均電流控制,,峰值電流的優(yōu)點為:1)暫態(tài)閉環(huán)響應比較快,對輸入電壓的變化和輸出負載的變化瞬態(tài)響應也比較快,;2)控制環(huán)易于設計,;3)具有簡單自動的磁平衡功能;4)具有瞬時峰值電流限流功能等,。但是峰值電感電流可能會引起系統(tǒng)出現(xiàn)次諧波振蕩,,許多文獻雖對此進行一定的介紹,但都沒有對次諧波振蕩進行系統(tǒng)研究,,特別是其產(chǎn)生原因和具體的電路實現(xiàn),,本文將對次諧波振蕩進行系統(tǒng)研究。
1 次諧波振蕩產(chǎn)生原因
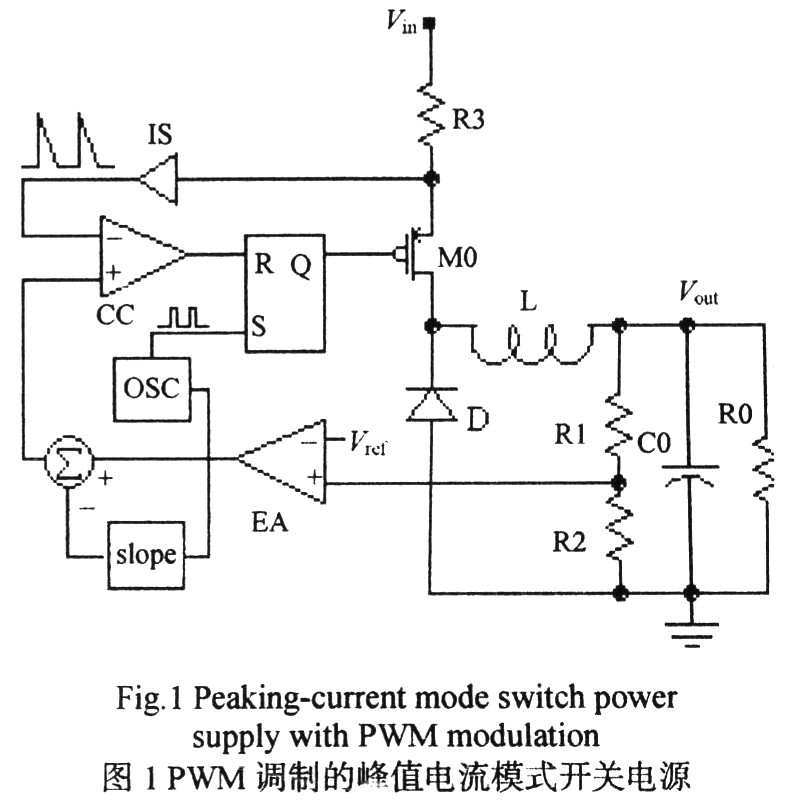
以PWM調制峰值電流模式開關電源為例(如圖1所示,,并給出了下斜坡補償" title="斜坡補償">斜坡補償結構),,對次諧波振蕩產(chǎn)生的原因從不同的角度進行詳細分析,。
查看原圖(大圖)
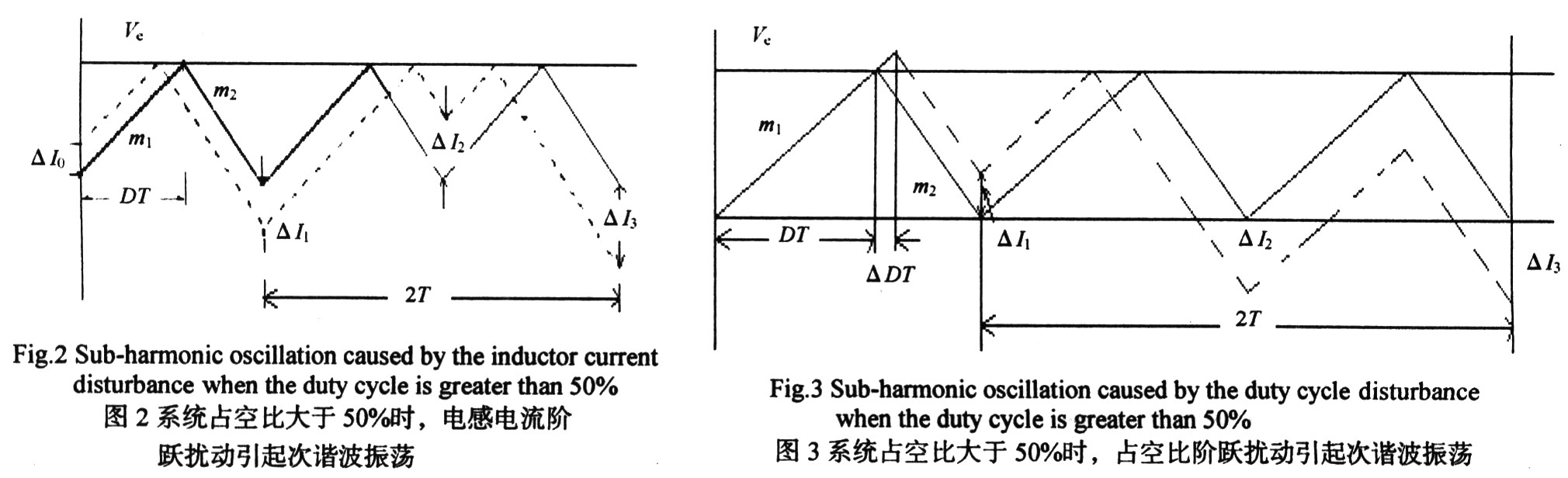
對于電流內環(huán)控制模式,圖2給出了當系統(tǒng)占空比大于50%且電感電流發(fā)生微小階躍△厶時的電感電流變化情況,,其中實線為系統(tǒng)正常工作時的電感電流波形,,虛線為電感電流實際工作波形??梢钥闯觯?)后一個時鐘周期的電感電流誤差比前一個周期的電感電流誤差大,,即電感電流誤差信號振蕩發(fā)散,系統(tǒng)不穩(wěn)定,;2)振蕩周期為開關周期的2倍,,即振蕩頻率為開關頻率" title="開關頻率">開關頻率的1/2,這就是次諧波振蕩名稱的由來,。圖3給出了當系統(tǒng)占空比大于50%且占空比發(fā)生微小階躍AD時電感電流的變化情況,,可以看出系統(tǒng)同樣會出現(xiàn)次諧波振蕩。而當系統(tǒng)占空比小于50%時,,雖然電感電流或占空比的擾動同樣會引起電感電流誤差信號發(fā)生振蕩,,但這種振蕩屬于衰減振蕩。系統(tǒng)是穩(wěn)定的,。
查看原圖(大圖)
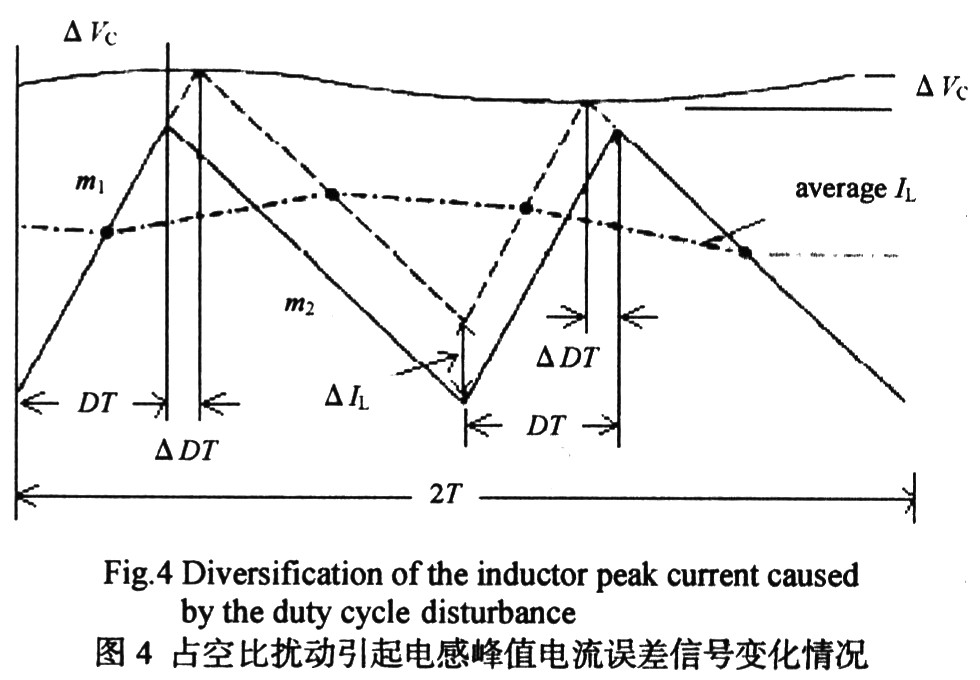
前面定性分析了次諧波振蕩產(chǎn)生的原因,,現(xiàn)對其進行定量分析。針對圖1,,圖4給出了占空比擾動引起電感峰值電流誤差信號變化情況,,其中Vc為誤差運放的輸出信號,當功率管MO導通即電感電流線性上升時,,Vc隨之增加,,反之當功率管M0關斷時,Vc隨之減小,。從圖4可以看出當占空比在連續(xù)2個時鐘脈沖下存在不對稱時,,系統(tǒng)將出現(xiàn)次諧波振蕩?,F(xiàn)推導△Vc與△IL的關系,,占空比擾動△D引起電感電流與誤差運放輸出電壓的變化值分別如式(1)和(2)所示,由式 (1)和(2)可推導出Vc與△IL的關系如式(3)所示:
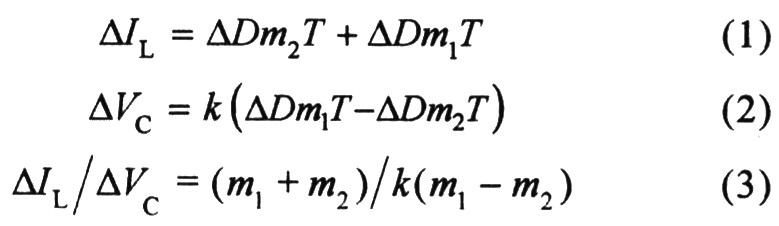
查看原圖(大圖)
式中:T為開關周期,;m1為峰值電流上升斜率,;m2為峰值電流下降斜率絕對值;七代表采樣電阻,。
由于次諧波振蕩頻率為開關頻率的1/2,,因此在1/2開關頻率處的電壓環(huán)路增益將直接影響電路的穩(wěn)定性。現(xiàn)推導圖1的電壓環(huán)路增益,,在誤差運放輸出端疊加斜坡補償后,,設誤差電壓從△Vc變?yōu)椤鱒e,,從而可推出△Vc與△Ve的關系,如式(4)所示,。由式(3)和(4)可得式(5),,在穩(wěn)態(tài)時可推出式 (6),將式(6)代入式(5)消去m1,,得式(7):
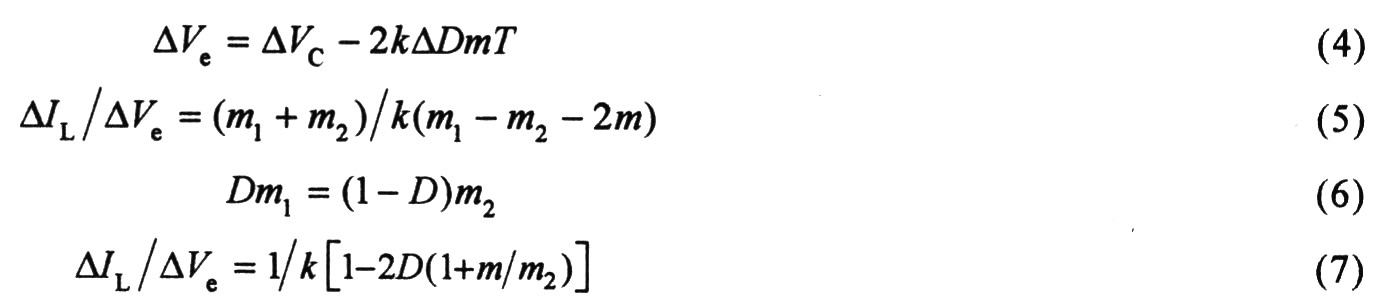
查看原圖(大圖)
查看原圖(大圖)
式中:m為下斜坡斜率,;2表示次諧波振蕩周期是開關頻率的2倍。
從圖4可以看出△IL是周期為2T的方波,,則第1個次諧波振幅應乘以4/π,。假設負載電容為C,則從誤差運放輸出端到電源輸出端的小信號電壓增益為
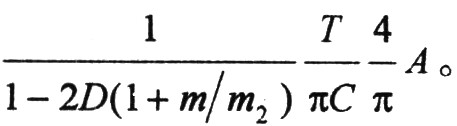
設誤差運放電壓增益為A,,則電壓外環(huán)環(huán)路增益為
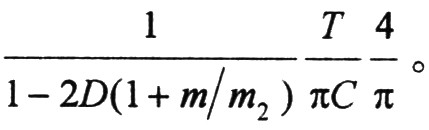
由環(huán)路穩(wěn)定性條件可知:在l/2開關頻率處,,環(huán)路相位裕度為零,此時若環(huán)路增益大于l,,系統(tǒng)就會發(fā)生次諧波振蕩,,因此誤差運放的最大增益為:
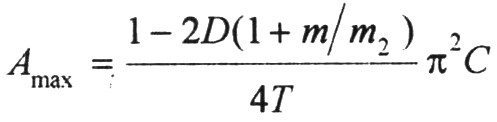 (8)
(8)
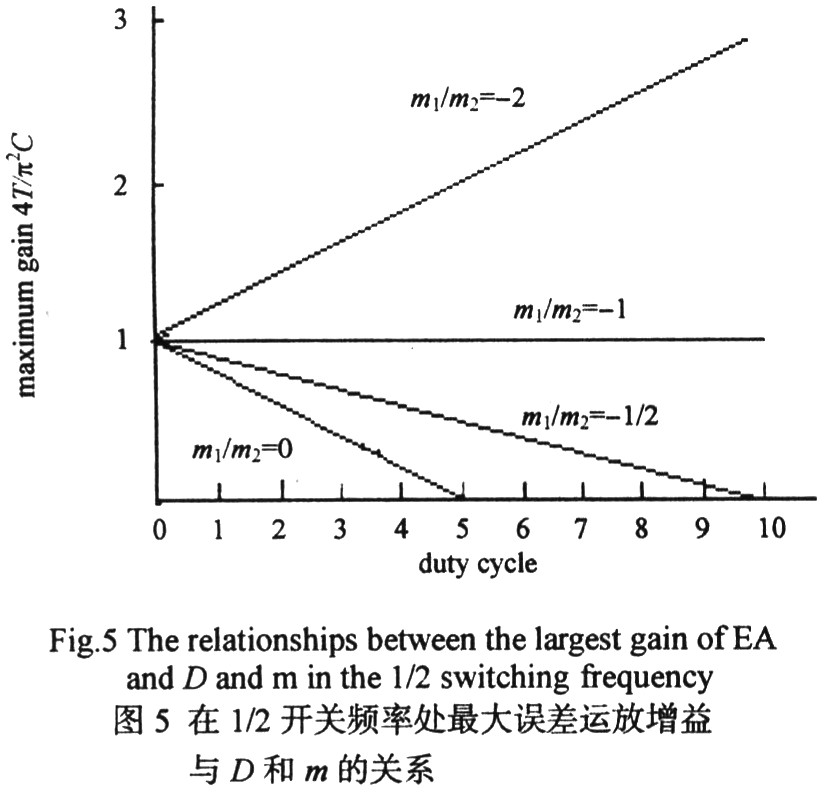
由式(8)可以明顯看出,誤差運放的最大增益是占空比D和斜坡補償斜率m的函數(shù),,歸一化的誤差運放最大增益與D和m的關系如圖5所示,。可以看出:m=O(無補償)時,,由于運放增益不能小于O,,當占空比大于或等于50%時,系統(tǒng)就會出現(xiàn)次諧波振蕩,;m=一m2/2時,,D=100%才出現(xiàn)次諧波振蕩,但在實際電路中D<100%時就會出現(xiàn)振蕩,;m=一m2時,,誤差運放最大增益與占空比無關。當繼續(xù)增大m時,,對環(huán)路的穩(wěn)定性影響不大,,但過補償會影響系統(tǒng)瞬態(tài)響應特性。
上文研究了電感電流信號變化波形對次諧波振蕩產(chǎn)生的原因及解決辦法,,現(xiàn)從s域(或頻域)角度對其進行更深入的研究,。設采樣電感電流i,通過采樣電阻Rs轉化成電壓,,i(k)表示第k時鐘下的電流擾動量,,△Ve(k+1)為第k+1時刻的電壓控制擾動量,得采樣保持的離散時間函數(shù):
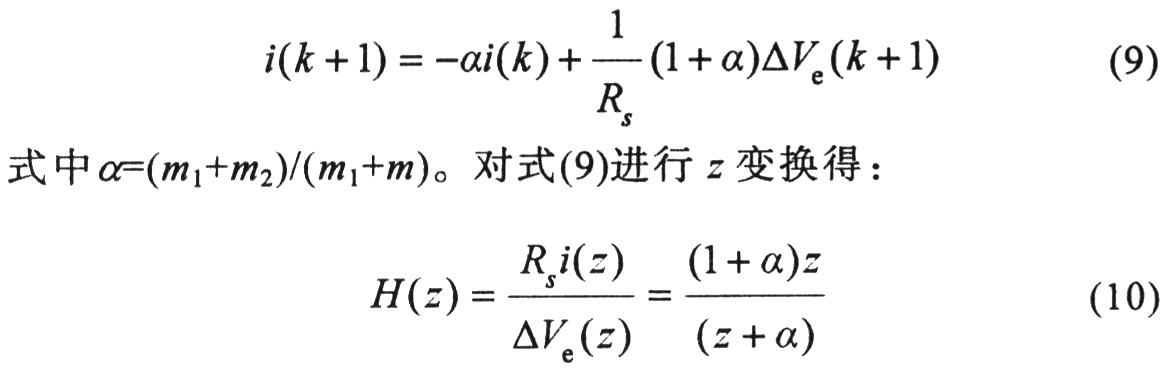
查看原圖(大圖)
由式(10)可知當沒有斜坡補償,,且m1
查看原圖(大圖)
式中s表示頻率,。esT可用PadE可用Pade進行二階近似:
查看原圖(大圖)
查看原圖(大圖)
式中Qs=2/[π(2/α-1)],,即阻尼系數(shù)為1/Qs=[π(m1-m2+2m)]/[2(m1+m2)]。式(13)即為電流環(huán)傳遞函數(shù),,斜坡補償前,,當m1
2 斜坡補償方式及電路實現(xiàn)
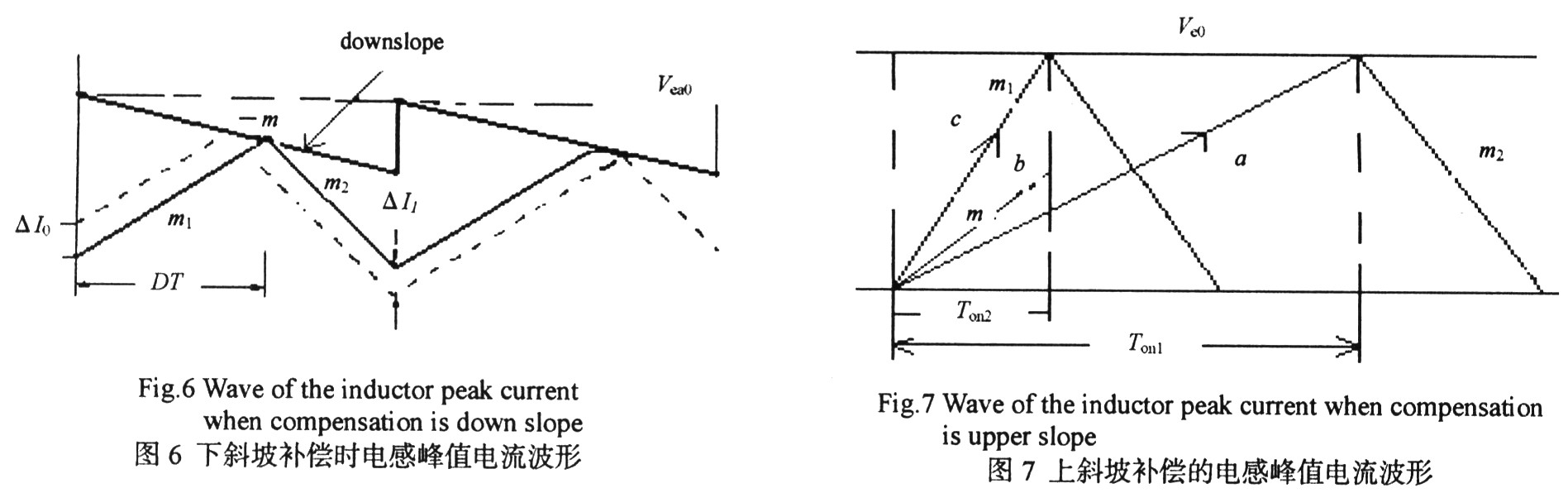
前文從幾個方面研究了次諧波振蕩產(chǎn)生的原因,,并且指出斜坡補償能防止系統(tǒng)出次諧波振蕩,現(xiàn)研究補償方式及其具體電路實現(xiàn),。開關電源斜坡補償分為上斜坡補償與下斜坡補償2種方式,。圖6為下斜坡補償原理,給出了下斜坡補償時占空比大于50%的電感峰值電流波形(電流微小擾動作為激勵信號),。與圖2相比,,僅Ve 從水平直線改為下斜坡。從圖6可以看出,,引入斜坡補償后,,電流誤差信號每經(jīng)過一個時鐘周期,幅度成比例衰減,,最后消失,。圖7為上斜坡補償原理,給出了占空比大于50%的電感峰值電流波形,。其補償原理就是在電感峰值電流a上疊加上斜坡補償電流b,,形成檢測電流c,使占空比小于50%,,穩(wěn)定系統(tǒng),。由于上斜坡補償電路實現(xiàn)相對簡單,一般采用上斜坡補償,。
對于斜坡補償,,斜率越大,振蕩衰減越快,,但補償斜率過大,,會造成過補償。過補償會加劇斜坡補償對系統(tǒng)開關電流限制指標的影響,,從而降低系統(tǒng)的帶載能力,;另一方面,過補償會影響系統(tǒng)瞬態(tài)響應特性,。通常選擇斜坡補償斜率需根據(jù)需要折中考慮,。對于Buck和Flyback轉換器,補償斜坡一般取峰值電流下降斜率 m2即Vout/L,,由于輸出電壓恒定,,所以補償值便于計算并恒定;對于Boost電路,補償斜坡也一般取峰值電流下降斜率m2,,即(Vout- Vin)/L但由于輸入電壓隨電網(wǎng)變化,,從而要求補償值跟隨輸入電壓的變化,此時若為了電路設計簡單,,強迫斜坡斜率固定,,則可能出現(xiàn)過補償或欠補償現(xiàn)象,降低電路性能并導致波形畸變,。
查看原圖(大圖)
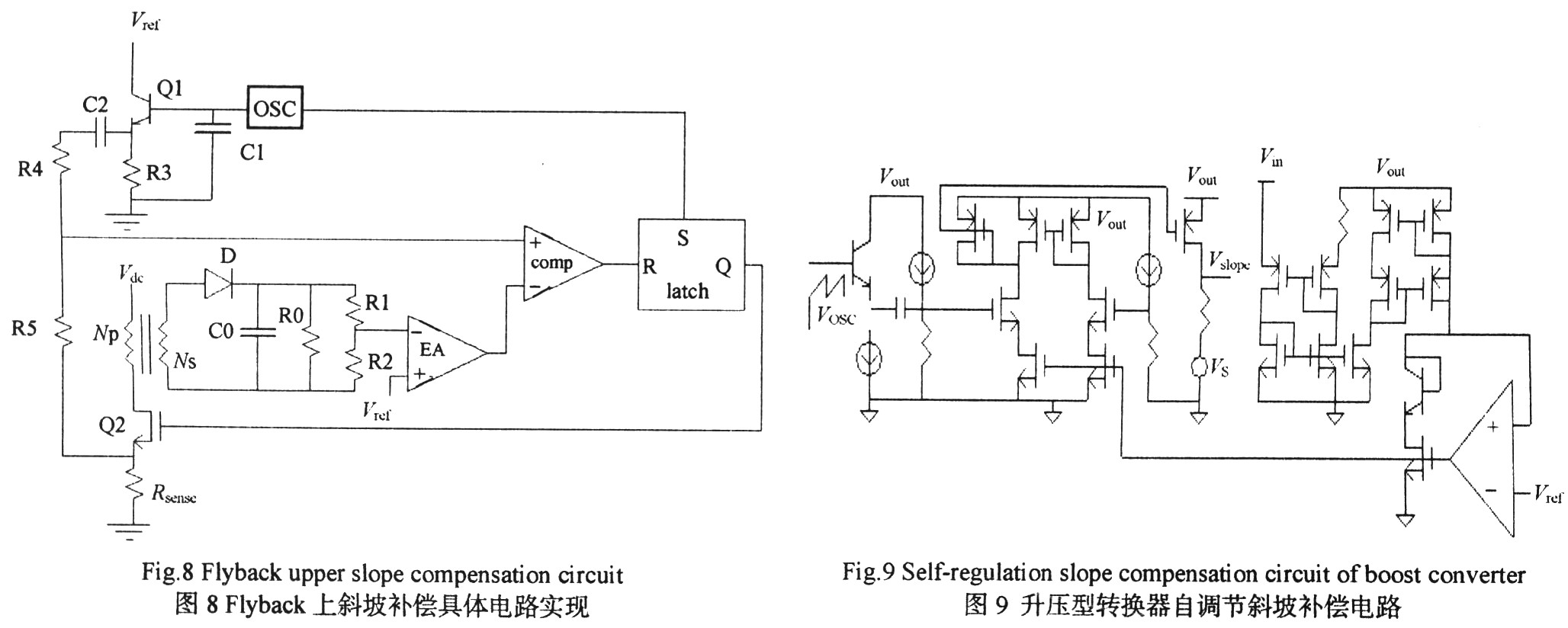
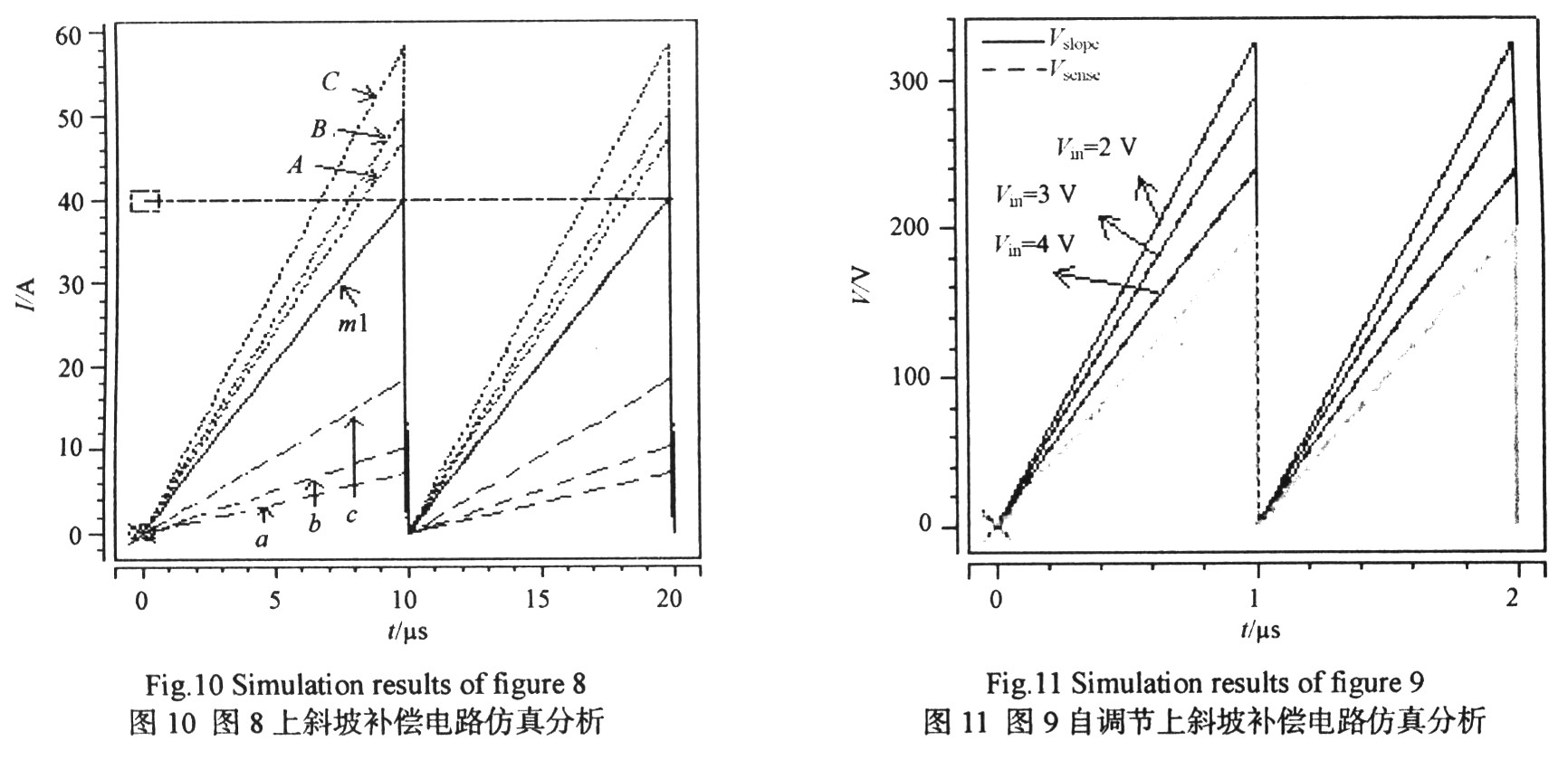
因Buck與Flyback轉換器斜坡補償原理電路實現(xiàn)基本相同,,因此本文只給出了一種上斜坡補償?shù)腇lyback斜坡補償電路(圖8所示)。圖9為本文第二作者提出的一種升壓型轉換器自調節(jié)斜坡補償電路,。采用Hspice仿真軟件分別對圖8和圖9進行仿真,,仿真結果分別如圖10和圖11所示。圖10的振蕩器頻率為100 kHz,。m1為檢測電流曲線,,其從0慢慢上升到40μA。虛線a,b和c代表具有不同斜率的斜坡補償信號,,線A,,B和C分別為疊加后的曲線。從圖10可看出:通過改變電阻R5和R4的比值,,可以得到具有不同斜坡的補償信號,。圖11中,Vsense為電感上的峰值電流流過檢測電阻所產(chǎn)生的電壓,,Vslope 為經(jīng)上斜坡補償后的檢測電流流過檢測電阻所產(chǎn)生的電壓,。從圖11可以看出,不同的輸入電壓對應不同的補償斜坡,,并且斜坡變化與(Vout-Vin)的變化成正比即達到了自調節(jié)功能,。
查看原圖(大圖)
查看原圖(大圖)
3 結論
本文對峰值電流模式開關電源的次諧波振蕩從定性和定量2個角度分別進行了系統(tǒng)研究,當占空比大于50%時,,系統(tǒng)的電流環(huán)在1/2開關頻率處出現(xiàn)振蕩,,引入斜坡補償后能保證電流環(huán)路增益的傳輸函數(shù)在1/2開關頻率處具有較好的相位裕度,保證系統(tǒng)穩(wěn)定,。最后分析了上斜坡補償和下斜坡補償2種避免次諧波振蕩的方法,,并基于3種最基本的開關電源拓撲(Buck,F(xiàn)lyback和Boost)給出了具體的斜坡補償電路及仿真結果,。