??? 摘 要： 采用VHDL語言,，在FPGA上實(shí)現(xiàn)了單精度" title="單精度">單精度浮點(diǎn)除法器" title="除法器">除法器的設(shè)計(jì)，通過采用SRT算法,、SD表示法,、常數(shù)比較法以及飛速轉(zhuǎn)換法，進(jìn)一步提高電路的運(yùn)算速度" title="運(yùn)算速度">運(yùn)算速度,。使用NC－sim和Maxplus2仿真軟件進(jìn)行前仿真和后仿真,，使用Synplify進(jìn)行邏輯綜合，采用EPF10K40RC208-3芯片,，對(duì)除法器進(jìn)行了仿真,。
??? 關(guān)鍵詞： 除法器? SRT? 單精度浮點(diǎn)? 數(shù)字循環(huán)法? 仿真
?
??? 在語音通信、圖像處理等領(lǐng)域中,，系統(tǒng)往往涉及大量的數(shù)據(jù)處理,，而且數(shù)據(jù)計(jì)算精度和實(shí)時(shí)性要求很高,，需要很高的浮點(diǎn)處理能力來提高系統(tǒng)的執(zhí)行效率。Soerquist等人[1]指出,，在四種基本浮點(diǎn)運(yùn)算中,，浮點(diǎn)除法的執(zhí)行速度最慢，處理器執(zhí)行浮點(diǎn)加法和浮點(diǎn)乘法時(shí),，一般需要2～3個(gè)機(jī)械周期,，而浮點(diǎn)除法則需要8到60個(gè)機(jī)械周期。然而,，在浮點(diǎn)運(yùn)算中浮點(diǎn)除法占的比例較小,。Oberman和Flynn認(rèn)為[2]在所有浮點(diǎn)指令中，浮點(diǎn)加法指令占55%,，浮點(diǎn)乘法大約占37%,，浮點(diǎn)除法大約占3%，與浮點(diǎn)加法和浮點(diǎn)乘法相比,，浮點(diǎn)除法的比例很小,。但是，這并不表示浮點(diǎn)除法對(duì)處理器性能的影響很小,，在因?yàn)楦↑c(diǎn)指令阻塞等待而引起的處理器性能下降的因素中,，浮點(diǎn)除法指令大約占40%，浮點(diǎn)加法大約占42%,，浮點(diǎn)乘法大約占18％,。由此可見，浮點(diǎn)除法雖然出現(xiàn)的頻率較低,，但對(duì)處理器整體性能有較大的影響,。因此設(shè)計(jì)一種執(zhí)行效率較高的浮點(diǎn)除法結(jié)構(gòu)對(duì)處理器性能的提高具有很重要的意義。
1 SRT算法的優(yōu)點(diǎn)
??? 在處理單精度浮點(diǎn)數(shù)時(shí),，處理除法器的算法主要有兩種：函數(shù)迭代法及數(shù)字循環(huán)法,。由于函數(shù)迭代法所提供的商的最低位不準(zhǔn)確，導(dǎo)致四舍五入操作無效,，不能滿足IEEE 754標(biāo)準(zhǔn)對(duì)精度的要求,，而且它不產(chǎn)生余數(shù)，循環(huán)部分的執(zhí)行復(fù)雜性程度較高,。Oberman和Flynn的研究[2]表明數(shù)字循環(huán)算法可以取得較好的延時(shí)和面積平衡,。數(shù)字循環(huán)算法是以加法和減法運(yùn)算為基礎(chǔ)的算法，需要多個(gè)循環(huán)周期,，但是,，該算法的實(shí)現(xiàn)比較簡(jiǎn)單，所需的硬件面積較小，功耗也較小,，非常利于芯片的設(shè)計(jì),。
??? 該算法的實(shí)現(xiàn)主要有三種方法：恢復(fù)余數(shù)算法、不恢復(fù)余數(shù)算法以及SRT[3](Sweeney,，Robertson and Tocher)算法。傳統(tǒng)的除法器采用恢復(fù)余數(shù)算法或不恢復(fù)余數(shù)算法,，但是這兩種算法的運(yùn)算速度較低,，每次循環(huán)僅能產(chǎn)生一位的商數(shù)字，需要較多的循環(huán)次數(shù)" title="循環(huán)次數(shù)">循環(huán)次數(shù)才能達(dá)到需要的指標(biāo),。在每次循環(huán)時(shí),，恢復(fù)余數(shù)算法都需要將被除數(shù)或部分余數(shù)與除數(shù)進(jìn)行比較，如果除數(shù)較大,，還需要將部分余數(shù)恢復(fù)到上一次循環(huán)的數(shù)值,。不恢復(fù)余數(shù)算法雖然不需要將部分余數(shù)恢復(fù)到原來的數(shù)值，但是商的數(shù)字集會(huì)出現(xiàn)負(fù)值,，最后需要額外的加法器,，將商的正數(shù)部分與負(fù)數(shù)部分相減。SRT算法是不恢復(fù)余數(shù)算法的擴(kuò)展,，具備了不恢復(fù)算法的優(yōu)點(diǎn),，而且每次循環(huán)可產(chǎn)生log2r位結(jié)果(r為基數(shù)），大大減少了循環(huán)的次數(shù),?；赟RT算法的優(yōu)點(diǎn)，并考慮到本除法器應(yīng)用在自動(dòng)語音編碼,，本文所設(shè)計(jì)的除法器采用SRT算法進(jìn)行除法運(yùn)算,。
??? SRT算法由下面的表達(dá)式來確定商和余數(shù)：
??? 
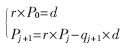
??? d表示除數(shù)；Pj+1表示第j次循環(huán)后的部分余數(shù),；r表示SRT算法的基,；qj+1表示第j次循環(huán)得到的商，qj+1的值由除數(shù)和部分余數(shù)組成的商數(shù)字選擇函數(shù)決定,。最后的商為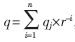
,，最后的余數(shù)為：
。
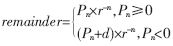2 單精度浮點(diǎn)除法器的設(shè)計(jì)
??? 本文是針對(duì)IEEE 754單精度浮點(diǎn)數(shù)據(jù)格式進(jìn)行的浮點(diǎn)除法器設(shè)計(jì),。IEEE 754單精度浮點(diǎn)格式：A=(-1)s×M×2E-127,，s表示符號(hào)位，E表示偏移碼,，E-127表示階碼,，M表示尾數(shù)。
??? 除法器運(yùn)算操作分四步進(jìn)行：
??? (1)確定結(jié)果的符號(hào)，對(duì)被除數(shù)和除數(shù)的符號(hào)位做異或操作,。
??? (2)計(jì)算階碼,，兩數(shù)相除，結(jié)果的階碼是被除數(shù)的階碼與除數(shù)的階碼的相減,。
??? (3)尾數(shù)相除,，采用SRT算法進(jìn)行尾數(shù)相除，被除數(shù)和除數(shù)的實(shí)際尾數(shù)都是24位數(shù),，即尾數(shù)實(shí)際為1.M,，最高位1是隱藏位。
??? (4)結(jié)果格式化,，將結(jié)果整合為單精度浮點(diǎn)格式的標(biāo)準(zhǔn),。
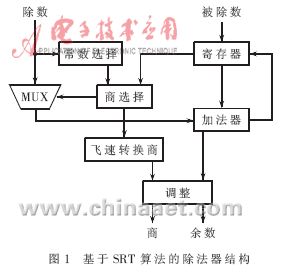
??? 在進(jìn)行尾數(shù)部分處理時(shí)，雖然被除數(shù)和除數(shù)的實(shí)際尾數(shù)均為24位,，但考慮到最后格式化以及商的數(shù)值的要求,，實(shí)際上需要進(jìn)行處理的位數(shù)為26位。因此,，根據(jù)SRT算法公式,，要使得循環(huán)次數(shù)減少，并且面積適中,，必須選擇適合的基數(shù),。而且每次循環(huán)時(shí)都需要與除數(shù)進(jìn)行比較，若26位數(shù)進(jìn)行比較,，則延時(shí)較大,，必須選擇位數(shù)較少的數(shù)值代替26位的除數(shù)。為了適應(yīng)自適應(yīng)語音編碼對(duì)速度的需求,，本文針對(duì)上述兩個(gè)需要進(jìn)行時(shí)序改善的地方,，設(shè)計(jì)了基4的SRT算法的除法器結(jié)構(gòu)，如圖1所示,。
??????????????????????????? 
2.1 基數(shù)的選擇
??? 考慮到部分余數(shù)以及基數(shù)實(shí)現(xiàn)的簡(jiǎn)單性,，本除法器選擇SRT算法的基數(shù)為2的冪次方?；鶖?shù)大小和所需的循環(huán)次數(shù)成反比,，基數(shù)越大，實(shí)現(xiàn)除法所需要的循環(huán)次數(shù)越少,。但是基數(shù)增加,，會(huì)導(dǎo)致商數(shù)字選擇函數(shù)復(fù)雜性的提高，而且商數(shù)字選擇函數(shù)往往處在關(guān)鍵路徑上,，其復(fù)雜度的增加無疑增加了每次循環(huán)的時(shí)間延遲,。另外，大基數(shù)使得產(chǎn)生所有可能商的乘積的硬件電路變得復(fù)雜，增大了每個(gè)循環(huán)周期,。因此,，在實(shí)際應(yīng)用中，SRT算法的基數(shù)一般限制在2或4,。相比較而言,，基4的性能較優(yōu)，每次循環(huán)產(chǎn)生的位數(shù)為基2的兩倍,，Oberman的研究[4]表明,，基4除法的速度幾乎是基2除法速度的2倍，而且更有利于進(jìn)一步優(yōu)化,，降低整體的時(shí)間延遲。因此,，在平衡面積和速度方面,，本除法器的SRT算法選取基4，這樣可以用較小的面積消耗換取較快的速度,。
2.2 商數(shù)字集
??? 由于SRT算法的基數(shù)選擇了4,，因此，商的數(shù)字集不再是{0,，1},，而是{0，…,，3},。在傳統(tǒng)的非冗余表示法中，商的每一位僅由一個(gè)正確的有效值表示,，因此在確定每一位商數(shù)字時(shí),，需要將部分余數(shù)和除數(shù)進(jìn)行完整的比較，即24位數(shù)的比較,，效率較低,。為了進(jìn)一步提高除法器的運(yùn)算速度，本除法器采用Avizienis[5]介紹的冗余商數(shù)字集SD,，它是一種對(duì)稱的冗余表示法,，商數(shù)字集表示為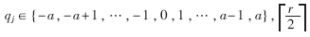
≤a≤r-1，冗余因子
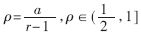,。在確定每位商數(shù)字時(shí),，僅需要將部分余數(shù)和除數(shù)進(jìn)行粗略的比較，不要求當(dāng)前循環(huán)確定的商準(zhǔn)確,，可由下次循環(huán)修正,，商的選擇余地較大，而且產(chǎn)生的所有可能商的乘積數(shù)目較少，可以簡(jiǎn)化商數(shù)字選擇函數(shù),。對(duì)于基4來說,，商數(shù)字集只有兩種選擇，最小冗余{-2,，-1,，0，1,，2}和最大" title="最大">最大冗余{-3,，-2，-1,，0,，1，2,，3},，Oberman的研究[4]表明采用最大冗余商數(shù)字集的商數(shù)字選擇函數(shù)速度比最小冗余的快20%,而且面積小50%，因此本除法器采用商數(shù)字集的最大冗余表示法,。
2.3 商數(shù)字選擇函數(shù)
??? 商數(shù)字選擇函數(shù)的功能是從商數(shù)字集中有效地選擇出正確的商數(shù)字,，它是除法器的核心。由于商數(shù)字集選擇了最大冗余,，因此商數(shù)字選擇公式如下：
????qj+1=k∈{-3,，-2，-1,，0,，1，2,，3}
??? 如果d(k-1)≤rp[j]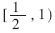
分解成若干個(gè)小區(qū)域
，
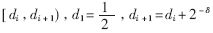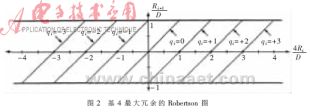
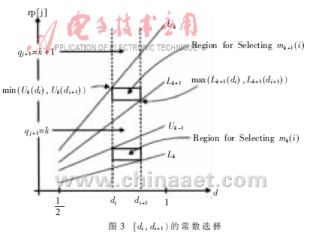
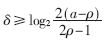,，然后判斷除數(shù)的合適區(qū)域,，再確定比較常數(shù)及每一位商數(shù)字所對(duì)應(yīng)的區(qū)域，最后根據(jù)部分余數(shù)確定每一位商數(shù)字,。常數(shù)選擇法如圖3[7]所示,。
??? 
?
??????????????????????????? 
????????????????????????????
???
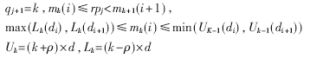??? 根據(jù)最大冗余基4的商數(shù)字集，區(qū)域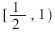
可以分成兩個(gè)小區(qū)域
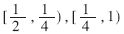,，相應(yīng)的比較常數(shù)集分別為{-3/2,，-1,，-1/2,，1/2，1,，3/2}和{-2,，-1，-1/2,，1/2,，1，2},，這些比較常數(shù)就是每位商數(shù)字所對(duì)應(yīng)區(qū)域的分界點(diǎn),。由所得到的兩個(gè)比較常數(shù)集可知，在確定商數(shù)字時(shí),，僅需要比較部分余數(shù)的高三位,，而不需要比較24位，產(chǎn)生的延時(shí)較小,，而且硬件實(shí)現(xiàn)比較簡(jiǎn)單,。
2.4 飛速轉(zhuǎn)換
??? SD表示的商數(shù)字集可以簡(jiǎn)化商數(shù)字選擇函數(shù)的實(shí)現(xiàn)，但是商數(shù)字集會(huì)出現(xiàn)負(fù)值,，最后需要一個(gè)加法器,，將商的正數(shù)部分與負(fù)數(shù)部分相減,。24位數(shù)的相減，位傳遞產(chǎn)生的時(shí)延比較大,，而且由于商數(shù)字的選取空間比較大,，會(huì)出現(xiàn)最后余數(shù)為負(fù)的現(xiàn)象，需要對(duì)其進(jìn)行修正,。同時(shí),，商也需要進(jìn)行操作，效率較低,。較好的轉(zhuǎn)換方法是飛速轉(zhuǎn)換法[8],，它采用移位的方法來完成SD表示的商數(shù)字集的轉(zhuǎn)換，而不采用相減的方法,，這樣就不存在借位的問題,，效率較高，可以降低時(shí)間延時(shí),。其轉(zhuǎn)換公式如下：
??? 
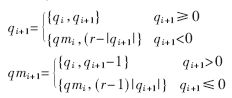
??? 當(dāng)完成最后一次轉(zhuǎn)換后,，需要根據(jù)最后余數(shù)的符號(hào)來選擇正確的商，如果最后余數(shù)為負(fù),，則商選擇qmi+1,，否則商選擇qi+1，則最后余數(shù)的選取不需要進(jìn)行修正,。
3 除法器的仿真實(shí)現(xiàn)
??? 根據(jù)所設(shè)計(jì)的結(jié)構(gòu),，編寫本單精度除法器的Verilog模型，在NC-sim進(jìn)行前仿真,，然后利用Synplify以Altera FLEX10K工藝庫(kù)的EPF10K40RC208-3芯片的參數(shù)進(jìn)行綜合,，最后完成的單精度除法器的規(guī)模為778個(gè)LUT，頻率為20.8MHz,。在Max+plus2進(jìn)行后仿真,，輸入除數(shù)為424A8000(1.01×2127)，被除數(shù)為3FA00000(1.10010101×2132),，運(yùn)算結(jié)果為42220000（1.010001×2132）,，余數(shù)為2F000000(0)，時(shí)序圖如圖4所示,，最后下載到芯片上運(yùn)行,。
???????????????????????????? 
??? 本文給出了單精度浮點(diǎn)除法器的設(shè)計(jì)，結(jié)合當(dāng)前比較流行的SRT算法與飛速轉(zhuǎn)換法對(duì)除法器的關(guān)鍵部分進(jìn)行時(shí)間延時(shí)的改善,，具有高精度性及較寬的運(yùn)算范圍,，可以滿足自適應(yīng)語音編碼的要求。
參考文獻(xiàn)
[1] SOERQUIST P,，LEESER M.Area and performance tradeoffs?in floating-point divide and square-root implementations.ACM Computing Surveys(CSUR),，1996,，28(3)：518-564.
[2] OBERMAN S，F(xiàn)LYNN M J.Division algorithm and implementations.IEEE transactions on computers,，1997,，46(8)：833-854.
[3] HARRIS D L，OBERMAN S F,，HOROWITZ M A.SRT?division architectures and Implementations.Computer systems
laboratory stanford university,，1997.
[4] OBERMAN S F.Design issues in high performance floating?point arithmetic units.PHD thesis，stanford university,，Electrical and electronic department,，1997，1.
[5] AVIZIENIS A.Signed-Digit number representations for fast?parallel arithmetic.IRE transactions on electronic computers,，EC-10：389-400,，1961，9.
[6] WILLIAMS T E,，HOROWITZ M.SRT division diagrams and?their usage in designing custom integrated circuits for division.Computer systems laboratory department of electrical?engineering stanford university.1986,，10.
[7] NIKMEHR H.Architectures for floating-point division.The?university of adelaide australia.2005，8.
[8] JAMES E.S.Digital computer arithmetic datapath design using verilog HDL.Kluwer academic publishers.2004：108-112.