??? 摘 要： 介紹一種新的多尺度分析" title="多尺度分析">多尺度分析方法,，并給出了一維EMD實(shí)現(xiàn)方法及其在信號(hào)處理中的應(yīng)用以及二維EMD實(shí)現(xiàn)方法及其在圖像處理" title="圖像處理">圖像處理中應(yīng)用,，該方法的應(yīng)用實(shí)例及分析過(guò)程,，同時(shí)分析了EMD的優(yōu)越性和應(yīng)用前景。
??? 關(guān)鍵詞： HHT? 多尺度分析? EMD

?

??? 自然界的絕大多數(shù)現(xiàn)象都是非線性,、非平穩(wěn)又或者伴有非線性,、非平穩(wěn)現(xiàn)象的過(guò)程，因而在信號(hào)分析" title="信號(hào)分析">信號(hào)分析中,，非平穩(wěn)信號(hào)分析是重要而常見(jiàn)的,，以往對(duì)它們的處理方法都或多或少存在缺點(diǎn)和不足^[1]。希爾伯特-黃變換HHT(Hilbert-Huang Transform)是繼小波變換之后,由美國(guó)科學(xué)家Norden E Huang等人于1998年提出的又一種多尺度分析的全新方法,。是一種適合處理非線性,，非平穩(wěn)信號(hào)的分析方法。非線性,、非平穩(wěn)信號(hào)分析的主要目的是要揭示信號(hào)時(shí)頻變化規(guī)律,。這種規(guī)律雖然目前可以通過(guò)短時(shí)傅立葉變換、小波變換等時(shí)頻分析法進(jìn)行分析,，但這些方法都是通過(guò)幅值譜來(lái)展示頻率變化規(guī)律的,，實(shí)質(zhì)都是以傅立葉變換(FT)為理論依據(jù)，因此不可避免地會(huì)因FT分析非線性,、非平穩(wěn)信號(hào)所帶來(lái)的缺陷，如出現(xiàn)虛假頻率,，因此所顯示的信號(hào)的頻率變化規(guī)律只能是粗略的,。此外，小波變換作為近年來(lái)廣泛受到關(guān)注和應(yīng)用的多尺度分析方法也存在不能克服的缺陷,，如最優(yōu)小波基的選取,、變換層數(shù)的確定，在不同小波基下處理所得的結(jié)果大不相同,。正是在這一背景下,，N.E.Huang等人創(chuàng)造性地提出了固有模態(tài)函數(shù)IMF(Intrinsic Mode Function)概念和經(jīng)驗(yàn)?zāi)Ｊ椒纸釫MD(Empirical Mode Decomposition)方法，再將信號(hào)分解所得的各階IMF進(jìn)行Hilbert變換,，形成時(shí)間頻率能量譜,，從而得到瞬時(shí)頻率并定義為Hilbert譜。美國(guó)NASA宇航中心將這種形式的Hilbert變換稱(chēng)為Hilbert-Huang變換（HHT）。這是一種以瞬時(shí)頻率為核心概念的方法,，理論上能精確給出信號(hào)中頻率隨時(shí)間變化的規(guī)律,，避免了虛假頻率等冗余現(xiàn)象，同時(shí)EMD的基隨信號(hào)自適應(yīng)地產(chǎn)生,，不同信號(hào)的基是惟一的,，不需要選擇。HHT方法一出現(xiàn)就受到廣大研究人員的青睞?，F(xiàn)已應(yīng)用到地球物理,、生物醫(yī)學(xué)、振動(dòng)工程,、機(jī)械工程,、故障檢測(cè)、圖像處理等領(lǐng)域,，實(shí)踐表明,，較依賴(lài)于先驗(yàn)函數(shù)基的Fourier分析和小波分析等方法，HHT更適合處理非平穩(wěn)信號(hào),，是一種具有自適應(yīng)性的時(shí)頻局部化多尺度分析方法,。將Nunes等人的一維EMD思想應(yīng)用于二維圖像處理中，使EMD的發(fā)展向前邁進(jìn)了一步,。本文給出了二維EMD的實(shí)現(xiàn)方法及應(yīng)用,。
1 EMD的實(shí)現(xiàn)及應(yīng)用
1.1 一維EMD和Hilbert的實(shí)現(xiàn)
??? Hilbert-Huang變換分為兩步：首先用經(jīng)驗(yàn)?zāi)B(tài)分解方法EMD獲得有限數(shù)目的固有模態(tài)函數(shù)IMF，然后再利用Hilbert變換和瞬時(shí)頻率方法獲得信號(hào)的時(shí)-頻譜——Hilbert譜,。由于瞬時(shí)頻率方法對(duì)任意信號(hào)不都適用, 它只對(duì)單分量信號(hào)(Monocomponent signal)才有意義,，而對(duì)于自然界和工程應(yīng)用領(lǐng)域，獲取的信號(hào)一般都不能滿(mǎn)足單分量信號(hào)的要求,，因此,，必須對(duì)信號(hào)進(jìn)行適當(dāng)?shù)奶幚怼＝?jīng)驗(yàn)?zāi)B(tài)分解方法(EMD)就是通過(guò)對(duì)信號(hào)進(jìn)行分解,，使之能夠表示為許多單分量信號(hào)之和,。在Hilbert-Huang變換中，為了把復(fù)雜的信號(hào)分解為簡(jiǎn)單的單分量信號(hào)的組合, EMD所獲得的固有模態(tài)函數(shù)(IMF)必須滿(mǎn)足下列兩個(gè)條件^[2-3]：
??? (1)在整個(gè)信號(hào)長(zhǎng)度上,，一個(gè)IMF的極值點(diǎn)和過(guò)零點(diǎn)數(shù)目必須相等或至多只相差一點(diǎn),。
??? (2)在任意時(shí)刻，由極大值點(diǎn)定義的上包絡(luò)線和由極小值點(diǎn)定義的下包絡(luò)線的平均值為零,，也就是說(shuō),，IMF 的上下包絡(luò)線對(duì)稱(chēng)于時(shí)間軸。滿(mǎn)足上述條件的IMF就是一個(gè)單分量信號(hào),。對(duì)于給定的信號(hào),，Huang所介紹的EMD方法是：
??? 首先找到信號(hào)的極大值和極小值,，通過(guò)三次樣條擬合，從而獲得信號(hào)的上包絡(luò)曲線env_max和下包絡(luò)曲線env_min, 計(jì)算上下包絡(luò)曲線的平均值曲線m1：m1=(env_max+env_min)/2,。設(shè)分析信號(hào)為x(t),，則：
??? x(t)-m₁=h₁
??? 從理論上講，h₁即為第一階IMF分量,，但由于樣條擬合h₁不一定滿(mǎn)足IMF的條件,，因此把h₁作為原始數(shù)據(jù)，重復(fù)上述步驟,，反復(fù)減均,，直到滿(mǎn)足IMF的條件為止。然后,，從原始信號(hào)中減去h₁即可獲得信號(hào)的逼近分量R₁,。
??? x(t)-h₁=R₁
??? 對(duì)R₁重復(fù)上面的過(guò)程, 就可以獲得第二階IMF分量。通過(guò)EMD方法對(duì)信號(hào)的一次次的篩分,，就可以獲得信號(hào)的多個(gè)IMF分量和一個(gè)逼近分量R_n,，從而信號(hào)可由下式表示：

???

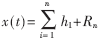
??? 因此，對(duì)任何一個(gè)信號(hào)x(t),，都可以將其分解為n個(gè)固有模態(tài)分量和1個(gè)殘余分量R_n之和,，其中，分量h₁,，h₂,，…h(huán)_n，包含了信號(hào)從高到低不同頻率段的成分,，且這些成分在頻域相互正交,，而R_n則表示了信號(hào)x(t)的整體趨勢(shì)。
??? 以上分解過(guò)程可以解釋為時(shí)空尺度濾波的過(guò)程,，每一個(gè)IMF分量都反映了信號(hào)的不同特征尺度的分量,，代表著信號(hào)的非線性非平穩(wěn)信號(hào)的內(nèi)在模態(tài)特征。若各階IMF都滿(mǎn)足Hilbert變換的前提條件,，可以對(duì)它們作Hilbert變換：

???

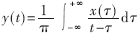
??? x(t)和y(t)形成一復(fù)共軛對(duì),，則其解析信號(hào)z(t)=x(t)+iy(t)=a(t)e^iθ(t)，幅值函數(shù)a(t)=相位函數(shù)

??? 再對(duì)相位函數(shù)求導(dǎo)即得IMF分量的瞬時(shí)頻率為：得到信號(hào)的Hilbert譜：更進(jìn)一步,，通過(guò)對(duì)時(shí)間積分可獲得信號(hào)的Hilbert邊際譜：

1.2 一維EMD的應(yīng)用
??? 這里選取三個(gè)正弦函數(shù)(一個(gè)頻率較低且幅值較大，另兩個(gè)頻率較高且幅值較小)和一個(gè)階躍函數(shù)的疊加信號(hào),，對(duì)其進(jìn)行四層EMD分解,，如圖1所示。圖1中,，從左到右是原始信號(hào),，從上到下是第一層到第四層IMF分量及四層分解后的殘余,。實(shí)驗(yàn)結(jié)果證明，信號(hào)經(jīng)EMD后得到了從高頻到低頻不同頻率段的成分,、殘余代表信號(hào)的主要趨勢(shì),。如果兩個(gè)相對(duì)高頻的正弦函數(shù)成分為噪聲，則得到的殘余成分非常接近于能量較大的低頻正弦函數(shù)成分和階躍函數(shù)成分的疊加,。如圖1(f)所示的一個(gè)波形,。實(shí)驗(yàn)結(jié)果很明顯地反映了EMD的去噪" title="去噪">去噪作用，而且這種去噪是完全自適應(yīng)性的處理,，效果理想,。從圖中也可看出，一維EMD存在邊界效應(yīng),，現(xiàn)已有一些研究人員提出了解決辦法,，如Huang提出的用特征波CW對(duì)原始信號(hào)進(jìn)行延拓的方法、基于神經(jīng)網(wǎng)絡(luò)技術(shù)對(duì)數(shù)據(jù)序列進(jìn)行延拓的方法,、基于AR模型的Levinson-Durbin算法的線性預(yù)測(cè)的方法以及采用最大熵譜(即Burg)估計(jì)進(jìn)行邊界延拓的方法,，一定程度上避免了邊界效應(yīng)。

?

?

2 二維EMD的實(shí)現(xiàn)及應(yīng)用
2.1 基于一維EMD提出二維EMD方法的實(shí)現(xiàn)
??? (1)求曲面局部極值點(diǎn)就是求出曲面上所有的比周?chē)R近點(diǎn)都大或都小的點(diǎn),。本文采用3×3（或5×5或7×7,，總之是奇數(shù)維）數(shù)組，通過(guò)中心點(diǎn)與周?chē)c(diǎn)比較分別確定極大值點(diǎn)和極小值點(diǎn),。對(duì)于一般邊界數(shù)據(jù)的處理,，因?yàn)橹挥性谝话氲泥徲騼?nèi)有數(shù)據(jù)，所以只能在1/2的鄰域區(qū)間內(nèi)尋找極值點(diǎn),。對(duì)于四個(gè)角處的數(shù)據(jù)處理,，則考慮1/4鄰域區(qū)間。
??? (2)極值點(diǎn)找出來(lái)之后,，要對(duì)各極大值點(diǎn)和各極小值點(diǎn)分別進(jìn)行曲面擬合,。本文采用三角剖分結(jié)合線性插值" title="插值">插值或立方插值進(jìn)行曲面擬合。三角剖分支持呈散射狀分布的數(shù)據(jù)點(diǎn)的插值且速度較快,。這樣,，經(jīng)插值后得到極大值點(diǎn)曲面包絡(luò)和極小值點(diǎn)曲面包絡(luò)，將兩曲面數(shù)據(jù)求平均得到均值包絡(luò)曲面數(shù)據(jù),。
??? (3)用原始曲面減去均值包絡(luò)曲面,。
??? (4)與一維EMD方法相似需計(jì)算終止條件，這里用max_ima表示減勻前曲面數(shù)據(jù)的最大值的絕對(duì)值,，用max_imd表示該曲面的均值包絡(luò)曲面數(shù)據(jù)的最大值的絕對(duì)值,，計(jì)算終止條件：，收斂速度較快些,。
2.2 二維EMD的應(yīng)用
??? 根據(jù)上述二維EMD的分解原理和分解方法,，本文對(duì)標(biāo)準(zhǔn)Lena圖像進(jìn)行五層的EMD分解,，其結(jié)果如圖2所示。圖2中,，從左到右是原始信號(hào),，從上到下是第一層到第五層二維IMF分量，依次得到從低頻到高頻的不同頻帶范圍內(nèi)的分量,。高頻分量代表圖像的細(xì)節(jié),，與現(xiàn)有的幾種提取圖像邊緣的方法相比，這里提取的細(xì)節(jié)更為全面,，同時(shí)又只攜帶了很少的能量,。用EMD將圖像分解成各層細(xì)節(jié)和輪廓（殘余）之后也為圖像進(jìn)一步處理（如圖像增強(qiáng)、圖像壓縮等）提供了新的前提,。在將圖像分解為高頻,、次高頻等分量的過(guò)程中，圖像中各點(diǎn)經(jīng)歷著提取自身的相對(duì)高頻,、次高頻的過(guò)程,，所以，相信基于這種方法的圖像處理效果與以往的處理方法相比會(huì)有所不同,，效果更自然,，有其獨(dú)特的視覺(jué)意義。

?

參考文獻(xiàn)
[1] HUANG N E，SHEN Z,，LONG S R,，et al.The empirical?mode decomposition method and the Hilbert spectrum for non-stationary time series analysis.Proc.R.Soc.Lond.A454，1998：903-995.
[2] WU Zhaohua,，HUANG N E.A study of the characteristics?of white noise using the empirical mode decomposition?method.Proc.Roy.Soc.London A,，Dec，2002.
[3] 鐘佑明,，秦樹(shù)人,，湯寶平.Hilbert-Huang變換中的理論研究[J]．振動(dòng)與沖擊，2002,，21(4)：13-17．