小波分析是最近十幾年來發(fā)展起來的一種新的時頻分析方法。它克服了短時傅里葉變換在單分辨率上的缺陷,，具有多分辨率分析的特點,，在時域和頻域都有表征信號局部信息的能力。小波包分析是小波分析的延伸,，其基本思想是讓信息能量集中,，在細節(jié)中尋找有序性，把其中的規(guī)律篩選出來，為信號提供一種更加精細的分析方法,。它將頻帶進行多層次劃分,，對多分辨分析沒有細分的高頻部分進一步分解，并能夠根據(jù)被分析信號的特征自適應地選擇相應頻帶,，使之與信號頻譜相匹配,，從而提高時一頻分辨率。我們可以根據(jù)小波包的分解特性,，利用小波包分解技術濾除干擾信號,。
1 小波包分析基本原理
1.1 小波變換
信號x(t)的連續(xù)小波變換定義為：
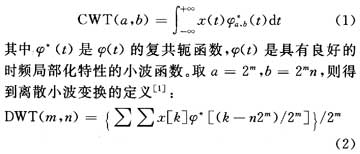
這個公式相當于信號x(t)通過了一個傳遞函數(shù)為
(ω)的有限沖激帶通濾波器(FIR)，選擇不同的m值,，相當于信號通過了不同的帶通濾波器,，這樣就可以把不同頻帶的信號分離開來。
利用濾波器組實現(xiàn)小波變換WT的過程分析如下：被分析信號通過鏡像濾波器后,，信號頻帶被劃分為低頻和高頻兩個頻帶,，其中的低頻信號通過向下采樣后，通過下一次鏡像濾波器分解,，再一次被劃分,，不斷重復這個過程，通過濾波器組就能夠把信號的頻帶劃分為(ω／2j,，ω／2j+1),，分解過程可以用圖1表示。
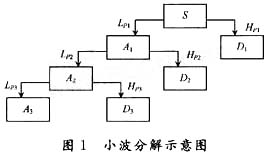
圖1中,，Ai,，Di分別表示信號的近似和細節(jié)，LPi,，HPi分別表示不同尺度的低,、高通濾波器。
1.2 小波包變換
小波包變換建立在小波變換的基礎上,，其定義為：
公式中的h0和h1相當于長度為2N的低通和高通濾波器,。
利用濾波器組實現(xiàn)小波包變換WPT的過程類似于WT變換，兩者不同之處在于WT濾波器組是對低頻頻帶不斷二進劃分,，而WPT是同時對高頻和低頻頻帶做二進劃分,，最后整個頻帶被劃分成均勻的頻帶。
分解過程也可以用小波包分解樹來表示,，如圖2所示,。
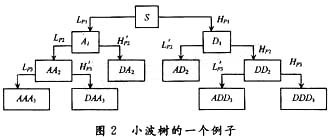
圖2中，LPi,，HPi,，L'Pi,，H'Pi分別表示不同尺度、不同分支的低,、高通濾波器,。在這里信號S可以表示為很多種分解方式，比如：
實際的處理過程一般是根據(jù)需要解決的問題和信號的能量分布,，來決定進一步分解的策略,。小波包的分解方式太多，對于一維信號,，每次分解把原系數(shù)分為兩組系數(shù)，那么對于長度為N的信號,，如果分解到L層,，那么共有α=2L種分解方式。每種分解方式對應一個小波樹,，如果引入某種判別方法,，從多個小波樹挑出符合一定標準的最優(yōu)小波樹，運算量也可以大幅度降低,。指導小波包分解的特征函數(shù)主要是信息的熵,。熵是度量信息規(guī)律性的量，主要的幾種熵有Shannon熵,、P階標準熵,、對數(shù)能量熵、閾值熵,、SURE熵,，其定義就不在此詳述了。
2 仿真分析實驗
在Matlab環(huán)境下,，利用Simulink工具箱將語音信號bluetooth.wav進行脈沖編碼調(diào)制ADPCM,，再經(jīng)過BPSK調(diào)制被周期為64的m序列直接相乘進行擴頻，擴頻后信號S1(t)的帶寬為896 kHz,；單音頻噪聲S2(t)的載頻為45 kHz,；信噪比為-15 dB，兩信號疊加得到W(t),，W(t)=S1(t)+S2(t),，如圖3所示。
語音擴頻信號混有單音頻噪聲前后的功率譜密度PSD如圖4所示,，受干擾前后的時域波形如圖5所示,。
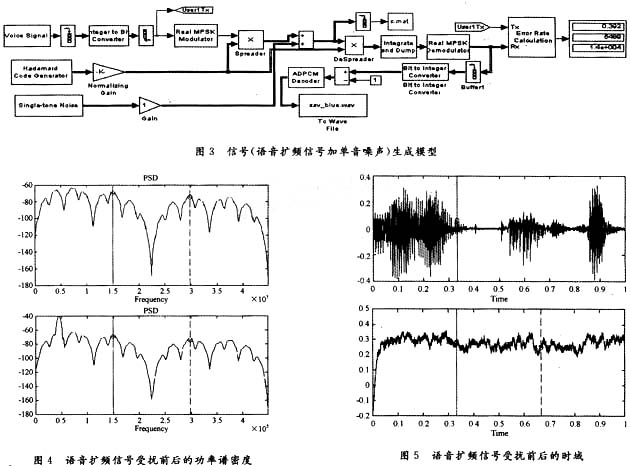
混有單音頻噪聲的語音擴頻序列經(jīng)過解擴、解調(diào)處理后的誤碼率為3.92e-1,，主觀上聆聽完全無法辨析語音內(nèi)容,。下面利用小波包分解技術去除單音頻噪聲，選取Shannon熵，依據(jù)原理公式(3),，(4)以及圖2所示的小波樹分解框圖,，在Matlab仿真環(huán)境中用wpdencmp函數(shù)，采用“db43”小波包作4層分解,，取全局域值5.035,，應用軟判決準則，提取擴頻序列de.mat,。由于小波樹能夠?qū)Ω叩皖l段均進行頻帶劃分,，因此能更有效地鎖定窄帶干擾分量。
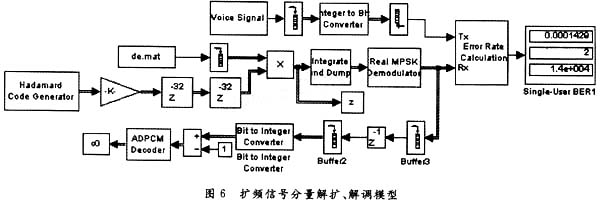
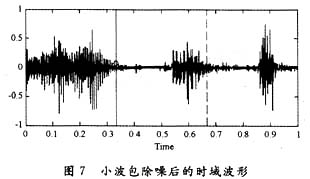
將de.mat數(shù)據(jù)解擴,、解調(diào),，其誤碼率為1.429e-4，提高了3個數(shù)量級,，性能大大改善,。將除噪后的數(shù)字音頻信號進行ADPCM解碼，得到的時域圖如7所示,，再次進行聆聽,，能夠較清晰地分辨語音內(nèi)容，只存在極少數(shù)的背景噪音,。如果還需進一步增強語音信息,，可以采用信號特征提取等處理方法去除其他噪聲，本文不再詳述,。
為了進一步突出小波包除噪效果,，我們采用同樣具有時域局部化特點的短時傅里葉變換方法代入實驗程序，其除噪后的語音時域波形圖如圖8所示,。
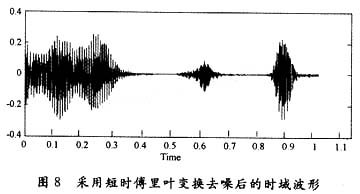
分別將圖7,、圖8與語音原始信號的時域波形圖相比，圖8損失了較多的語音細節(jié),，從主觀聆聽效果來看,，也沒有小波除噪后的還原效果好。短時傅里葉變換雖能描述某一局部時間段上的頻率信息,，但由于整個過程只加了相同的窗函數(shù),，所以它不適應信號頻率高低變化的不同要求。
3 結 語
本文討論了基于小波包分析技術去除語音擴頻信號單音頻干擾的原理和應用,。小波包變換的任意多尺度分解特性和良好的時,、頻域局部化特性可被用于迅速跟蹤和確定信號分量的時、頻域位置,，尤其適用于擴頻信號混有窄帶干擾的情況,。仿真實驗結果證明利用小波包分析能夠獲得滿意除噪效果,。