在衛(wèi)星地面綜合測試系統(tǒng)中,，遙測前端設備是綜合測試系統(tǒng)與衛(wèi)星的主要信息接口之一，負責下行遙測數(shù)據(jù)采集,，與其他專用設備及主控計算機一起完成對衛(wèi)星遙測分系統(tǒng)的測試^[1],?？删幊绦l(wèi)星信號模擬源作為遙測前端設備的一部分,，主要功能是產生遙測數(shù)據(jù)的副載波已調信號。為提供不同信噪比的副載波已調信號,，需要參數(shù)可變的高斯白噪聲,。因而高斯白噪聲的性能是決定可編程衛(wèi)星信號模擬源性能的重要方面之一。
　　目前,，為獲得參數(shù)可調的高斯白噪聲,，一般采用數(shù)字方法產生。數(shù)字方法產生分為兩步：先產生均勻分布" title="均勻分布">均勻分布的白噪聲,，然后通過均勻分布的白噪聲獲得高斯白噪聲,。在這兩步中均有多種方法可以選擇。
1 均勻分布白噪聲生成算法的選擇
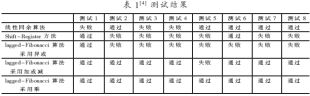
　　目前,，有三種常用的均勻分布白噪聲生成算法：線性同余算法,、Shift-Register方法和Lagged-Fibonacci算法。

　　對三種算法的性能進行測試,包括隨機數(shù)在分布上的均勻性,、隨機數(shù)在隨機序列中分布的均勻性和隨機序列中子序列的依賴關系等內容,。結果如表1所示。其中,，滿足測試要求視為通過,，不滿足視為失敗。
　　可見,，就性能而言,，lagged-Fibonacci算法采用乘最好，lagged-Fibonacci算法采用加或減次之,。
　　從實現(xiàn)角度,，Shift-Register方法、lagged-Fibonacci算法采用異或和lagged-Fibonacci算法采用加或減只需要移位,、異或和加減法等操作,，適合FPGA實現(xiàn),。而線性同余算法和lagged-Fibonacci算法采用乘需要乘法操作，適合DSP實現(xiàn),。
　　根據(jù)以上判斷,，結合實際硬件情況，采用lagged-Fibonacci算法的加或減,。

2 均勻分布白噪聲產生高斯白噪聲算法的選擇
　　目前,，比較常用的有地址方法和公式方法。
　　(1)采用地址方法產生高斯噪聲
　　根據(jù)定理：若給定任何隨機變量X的累積分布函數(shù)為F(X),，則Y= F(X)是在(0,，1)內均勻分布的隨機函數(shù)。這樣,，當隨機變量X為高斯分布,，Y為均勻分布白噪聲，利用X與Y的映射關系獲得高斯白噪聲,。
　　(2)采用公式方法產生高斯噪聲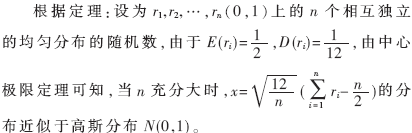

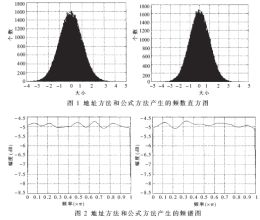
　　通過Matlab仿真,，可以獲得兩種方法產生高斯白噪聲的性能，如圖1和圖2所示,。

　　可見,，就性能而言，兩者差不多,。
　　從實現(xiàn)角度,，前者具體實現(xiàn)時，產生高斯白噪聲速度比較快,，但需要使用Rom來保存映射關系,。為獲得較高性能的高斯白噪聲，需要大容量的Rom,。后者具體實現(xiàn)時,，不需要使用大容量的內存，但需要n個均勻白噪聲才可以產生一個高斯白噪聲,，產生速度比較慢,。
　　根據(jù)以上判斷，結合實際硬件情況,，采用公式方法,。
3 實際使用
　　綜合前面，在FPGA采用lagged-Fibonacci算法(采用加)和公式方法的組合來實現(xiàn)高性能高斯白噪聲,?？紤]到加入對高斯白噪聲的均值和方差的控制，實現(xiàn)框圖如圖3所示,。

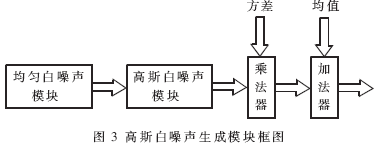
　　均勻白噪聲模塊中,，使用lagged-Fibonacci算法(采用加),。這里使用的算法表達式：F(17,5,+)mod 2³²。具體步驟如下：
　　初始化：I=17,J=5及L(n),n=1,…,，17
　　操作：L(I)←L(I)+L(J)
　　輸出L(I)作為均勻白噪聲
　　I←I-1;if I=0,I←17
　　J←J-1;if J=0,J←17
　　重復操作
　　高斯白噪聲模塊中,，公式方法取n＝12時，分布已經接近高斯分布了,。這時表達式為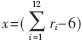：,。即對產生的12個均勻白噪聲按表達式進行操作來獲得高斯白噪聲。
　　在獲得高斯白噪聲后,，通過乘法器和加法器實現(xiàn)高斯白噪聲方差和均值的調節(jié)就得到了參數(shù)可調的數(shù)字高斯白噪聲,。因為對高斯分布x，通過變換y=μ+σx,，可以獲得均值為μ,、方差為σ2的高斯分布y。
　　在Altera的Cyclone中實現(xiàn)該數(shù)字高斯白噪聲所使用的資源如圖4所示,。

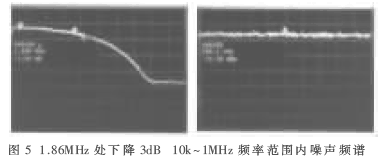
　　該高斯白噪聲經過低通濾波,、D/A轉換和模擬低通濾波得到模擬高斯白噪聲。該噪聲通過頻譜儀測量的實際性能如圖5所示,。可見,，該噪聲是限帶高斯白噪聲,，且在低頻段比較平坦，不超過1個dB,。滿足可編程衛(wèi)星信號模擬源的需要,。

　　總之，采用lagged-Fibonacci算法(采用加)和公式方法的組合可以實現(xiàn)高性能的高斯白噪聲,。包含該功能模塊的可編程衛(wèi)星信號模擬源已在相關衛(wèi)星測試部門中使用,。
參考文獻
1 Lehmer D.H. Mathematical methods in large-scale computing units. in Proc. 2nd Symposium on LargeScale Digital Calcu-lating Machinery, Harvard University Press: Cambridge, Mas-sachusetts, 1949:141～146
2 Golomb Ｓ Ｗ, Shift Register Sequences． Revised Edition． Aegean Park Press. Laguna Hills. California, 1982
3 Knuth D E, The art of computer programming, vol.2:Semin- umerical Algorithms, Second edition, Addison-Wesley,Read-ing,Massachusetts,1981
4 Marsaglia G. Ａcurrent view of random number generators. In Computing Science and Statistics: Proceedings of the XVIth Symposium on the Interface, 1985:3～10