0 引言

    大數(shù)據(jù)處理項目中,，資源消耗最為突出的是數(shù)據(jù)的收集和預處理，大約占項目資源支出的80%,，其中數(shù)據(jù)預處理工作量就要占60%左右^[1],。究其原因,，是因為實際應用系統(tǒng)收集數(shù)據(jù)時,，由于數(shù)據(jù)源的區(qū)別,、考慮因素不同及數(shù)據(jù)收集工具和數(shù)據(jù)傳輸問題等造成收集到的數(shù)據(jù)存在數(shù)據(jù)不完整、重要屬性缺失,、有噪聲和數(shù)據(jù)不一致等問題。要得到高質量的決策,，必然要求高質量的數(shù)據(jù),，所以數(shù)據(jù)預處理在數(shù)據(jù)分析工作量中占比最大，目的是給數(shù)據(jù)挖掘提供準確,、一致,、及時、權威的數(shù)據(jù)集,。數(shù)據(jù)預處理工作包括缺失值（空值）處理,、異常值處理、數(shù)據(jù)集成和數(shù)據(jù)規(guī)約,，其中數(shù)據(jù)規(guī)約是影響大型數(shù)據(jù)集預處理效果的主要瓶頸,。文獻[2]中提出基于聚類方法實現(xiàn)數(shù)據(jù)分層；文獻[3]-[4]中提出離群值檢測進行異常值處理,，進而數(shù)量規(guī)約,；文獻[5]-[6]中提出基于相似連接實現(xiàn)數(shù)據(jù)并行處理；文獻[7]-[9]提出了選用二維離散小波進行維度規(guī)約的數(shù)據(jù)預處理,；文獻[10]-[11]提出了針對稀疏數(shù)據(jù)進行數(shù)量規(guī)約的方法,。而針對存在相關性的多個變量，目前廣泛使用主成分分析(Principal Component Analysis,，PCA)方法進行降維,，從而使用較少的綜合指標來代表原變量中的各類信息，降低數(shù)據(jù)分析的復雜性,。

1 主成分分析PCA

    PCA的思想是將n維特征映射到k維(k<n)全新的正交特征(即主成分)上^[12],。其算法描述為：

    (1)輸入：n維特征數(shù)據(jù)集,；

    (2)計算樣本均值：

    (3)計算樣本方差S²：

    (7)得到降序排列的前k個λ_i對應的特征向量z_i組成的矩陣；

    (8)輸出：轉換到k個特征向量構建的新空間數(shù)據(jù)集,。

    由算法描述可知,，PCA方法即通過基變換實現(xiàn)降維。為了保證最優(yōu)變換,，PCA采用最大方差來確?；Ａ粜畔⒘康淖畲蠡?/p>

    使用PCA方法進行數(shù)據(jù)維規(guī)約時,，計算易于實現(xiàn),，只需要考慮原數(shù)據(jù)集的協(xié)方差矩陣大小，且k個主成分各自獨立^[13],。但PCA方法降維后,，主成分的各個特征解釋性有所降低，而且未被選擇的非主成分也可能含有對樣本差異的重要信息,，從而造成新的數(shù)據(jù)不完整,。

2 改進的PCA數(shù)據(jù)預處理方法

    使用PCA方法進行維規(guī)約時，首先需要對原數(shù)據(jù)集中的數(shù)據(jù)中心化,，其后也沒有人為設定參數(shù)或參照經(jīng)驗模型進行計算,，從而保證結果和數(shù)據(jù)相關，且獨立于用戶^[14],。由于均值易受極端值影,，簡單地使用與均值相減實現(xiàn)數(shù)據(jù)中心化是造成映射所得主成分的特征解釋性降低的原因之一。為了解決這一問題,，在對數(shù)據(jù)中心化時,，用加權規(guī)范化均值來代替均值實現(xiàn)數(shù)據(jù)中心化。加權規(guī)范化均值計算公式為：

其中,，I_d為數(shù)據(jù)集中的元素,，d為元素與均值差，w_d為每個元素對應d所分配的權值,，滿足∑w_d＝1,。

    改進后的PCA算法描述為：

    (1)輸入：n維數(shù)據(jù)集X={x₁，x₂,，…,，x_n}；

    (5)計算目標函數(shù),，其中v為單位向量：

    (6)得到max(f(v))的必要條件為Cv=λv,，則v為協(xié)方差矩陣的特征向量，其保存的信息量為特征值λ；

    (7)將協(xié)方差矩陣C對角化,，得到n個不同的特征值λ_i,，降序排列；

    (8)while(k<=n){

    (9)輸出：映射到新基集的數(shù)據(jù)集,。

3 算法驗證實驗

3.1 原始數(shù)據(jù)集概況

    實驗采用的數(shù)據(jù)集為長江流域夾江揚州三江營點位南水北調東線取水口斷面2018年52期水質自動監(jiān)測數(shù)據(jù)共364條,，水質監(jiān)測指標包括PH值、溶解氧DO,、高錳酸鉀指數(shù)CODMn,、氨氮 NH3-N、總磷TP,、總氮TN和總有機碳TOC共7個變量,，數(shù)據(jù)集片段如圖1所示。

3.2 數(shù)據(jù)中心化處理

    PCA方法對每個特征變量求均值,，即計算=xi-,，得到中心化后的數(shù)據(jù)集片段如圖2所示。

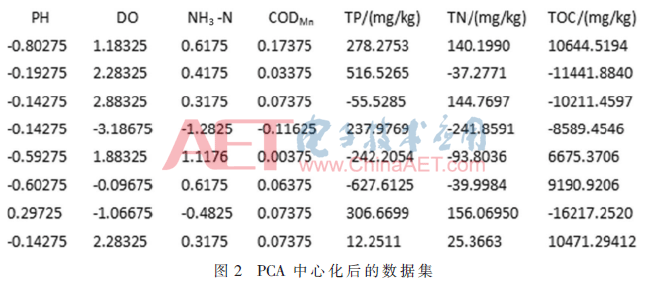
3.3 基于協(xié)方差矩陣的特征值確定主成分數(shù)量

    根據(jù)計算Rayleigh商和Cattell碎石檢驗原則,，使用改進PCA方法前后,，基于特征值對應的主成分選擇如圖4所示。

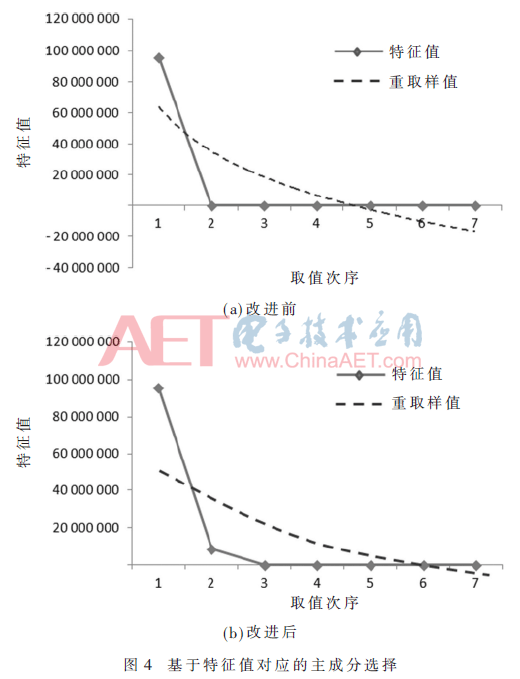
    由圖4(a)可知,，根據(jù)特征值對應選擇第1,、2、3和7個特征變量即可以表示數(shù)據(jù)集,，數(shù)據(jù)集由346×7降為346×4，且變量TOC和CODMn,、TN和NH3-N相關性較強,，但注意到變量TP沒有被解釋。

    由圖4(b)可知,，根據(jù)特征值對應選擇第1,、2、3,、4和7個特征變量即可以表示數(shù)據(jù)集,，數(shù)據(jù)集由346×7降為346×5，且變量TOC和CODMn,、TN和NH3-N相關性較強,，可以進行合并，并且沒有丟失變量TP的特征數(shù)據(jù),。

3.4 根據(jù)特征向量矩陣生成新數(shù)據(jù)集

    將特征值對應的特征向量構造矩陣,，得到數(shù)據(jù)降維轉換基，轉換前后數(shù)據(jù)集特征值示意圖如圖5所示。

    由圖5可知,，使用PCA方法進行降維處理后,，仍然可以保留原始數(shù)據(jù)集的大部分變量特征值，但實驗證明改進后的PCA方法尋找主成分更為謹慎,，對特征特征值描述更加清晰,。

4 結論

    主成分分析(PCA)是通過正交變換將n個可能相關的變量轉換為k個（k<n）不相關的變量，從而尋找到代表原數(shù)據(jù)集的主成分變量的一種統(tǒng)計方法,，是目前使用最廣泛的數(shù)據(jù)維規(guī)約算法,。理想的PCA方法使用要求最大方差和最少非主成分數(shù)據(jù)丟失，故使用PCA方法時要關注生成的協(xié)方差矩陣質量和特征值的選取數(shù)量,。中心化數(shù)據(jù)時將均值計算轉變?yōu)榧訖嘁?guī)范平均值的計算,，可以充分考慮各變量特征值的統(tǒng)計性能，保證生成的協(xié)方差矩陣質量,。通過Rayleigh商和Cattell碎石檢驗原則可以選擇更合理的特征值數(shù)目,，盡可能避免出現(xiàn)非主成分含有對樣本差異的重要信息丟失。實驗結果表明,，改進后的PCA算法更能保證數(shù)據(jù)完整性,，雖然可能會降低維規(guī)約的效率，但數(shù)據(jù)完整是高質量的數(shù)據(jù)源首先應該考慮的,。

參考文獻

[1] 曾祥坤,，張俊輝，石拓,，等.基于主題提取模型的交通違法行為文本數(shù)據(jù)的挖掘[J].電子技術應用,，2019，45(6)：41-45.

[2] 文若晴,，馬昂,，潘曉.基于密度聚類的簽到軌跡大數(shù)據(jù)分層預處理研究[J].計算機應用與軟件，2019,，36(3)：20-28.

[3] ZHANG Y,，MERATNIA N，HAVINGA P.Outlier detection tech-niques for wireless sensor networks：a survey[J].IEEE Com-munications Surveys ＆ Tutorials,，2010,，12(2)：159-170.

[4] LEI P R.A framework for anomaly detection in maritime traj-ectory behavior[J].Knowledge and Information Systems，2016,，47(1)：189-214.

[5] 郭方方,，潮洛蒙，朱建文.基于相似連接的多源數(shù)據(jù)并行預處理方法[J].計算機應用,，2019,，39(1)：57-60.

[6] CHEN Y F，ZHAO X，HE P J,，et al.BMGSJoin：a MapReduce based graph similarity join algorithm[J].Pattern Recognition & Artificial Intelligence,，2015，28(5)：472-480.

[7] 張璽君,，袁占亭,，張紅，等.交通軌跡大數(shù)據(jù)預處理方法研究[J].計算機工程,，2019,，45(6)：26-31.

[8] 崔光照，曹祥,，張華.基于小波變換的基因表達數(shù)據(jù)去噪聚類分析[J].信號處理,，2005，21(s1)：463-466.

[9] SU H,，ZHENG K,，WANG H，et al.Calibrating trajectory data for similarity-based analysis[C].ACM SIGMOD International Conference on Management of Data.ACM,，2013：833-844.

[10] 李志平,，付冬梅，穆志純.基于稀疏數(shù)據(jù)規(guī)約的CMAC大氣腐蝕數(shù)據(jù)補償方法[J].計算機應用研究,，2016,，33(9)：2645-2647.

[11] TAGHAVIPOUR A，F(xiàn)OUMANI M S,，BOROUSHAKI M.Implementation of an optimal control strategy for a hydraulic hybrid vehicle using CMAC and RBF networks[J].Scientia Iranica,，2012，19(2):327-334.

[12] 范葉平,，李玉,，楊德勝，等.基于深度集成學習的人臉智能反饋認知方法[J].電子技術應用,，2019，45(5)：5-8,，13.

[13] 謝霖銓,，徐浩，陳希邦,，等.基于PCA的決策樹優(yōu)化算法[J].軟件導刊,，2019，18(9)：69-71,，76.

[14] 張云龍.基于PCA的高維流式數(shù)據(jù)聚類算法[J].電子技術與軟件工程,，2019(8)：175-176.

作者信息:

陳  燕1，陳亞林2，鄭  軍1

(1.貴陽學院 數(shù)學與信息科學學院,，貴州 貴陽550002,；2.南京財經(jīng)大學 管理科學與工程學院，江蘇 南京210046)