0 引言

    OFDM技術(shù)以其頻譜利用率高、能有效對抗頻率選擇性衰落以及多徑干擾等優(yōu)勢,被廣泛應(yīng)用于WiMax,、WiFi,、LTE和DVB等多種高速傳輸系統(tǒng)中。但是，這種技術(shù)對符號定時和載波偏差特別敏感^[1-2],。因此,，定時和頻率同步算法的研究成為OFDM技術(shù)的關(guān)鍵問題。

    目前,，關(guān)于OFDM系統(tǒng)的同步算法可以分為三類：基于循環(huán)前綴的算法^[3],、基于訓(xùn)練序列的算法^[4-12]和盲同步算法^[13]?；谘h(huán)前綴的算法主要利用循環(huán)前綴的冗余信息進行同步估計,，算法定時準確性低；而盲同步算法一般計算較為復(fù)雜,可實現(xiàn)性較低,；基于訓(xùn)練序列的算法，主要利用序列的相關(guān)特性設(shè)計定時度量函數(shù),，定時精確度較高,，且計算復(fù)雜度低，應(yīng)用較為廣泛,。此類算法較為典型的是S&C算法^[4],，但是定時峰值存在“平臺”效應(yīng)。之后,，MINN H^[5]對訓(xùn)練序列結(jié)構(gòu)進行改進,，消除了S&C算法判決曲線的平坦特性。PARK B^[6]利用訓(xùn)練序列的共軛對稱特性,，使定時峰值更加尖銳,，但是存在副峰值，而且無法估計頻偏,。ZHOU E^[7]等人在S&C算法和文獻[6]算法的基礎(chǔ)上,，將延時和對稱自相關(guān)結(jié)合，提高了定時估計性能,，但是計算量大,，也無法進行頻偏估計。文獻[8-10]對訓(xùn)練序列進行加權(quán)處理,，能得到尖銳的定時峰值,，但是直接影響到頻偏估計的準確性。文獻[11]的定時同步需要在頻偏估計之后完成,，導(dǎo)致定時性能容易受到頻偏影響,，而且小數(shù)倍頻偏估計范圍較小。文獻[12]在定時準確的基礎(chǔ)上提高了頻率同步性能,，但是整數(shù)倍頻偏估計需要在頻域進行,，增加了計算復(fù)雜度。由上可知，已有的同步算法難以同時兼顧定時同步,、頻偏估計以及算法的復(fù)雜度這三者的性能,。

    因此，針對目前OFDM系統(tǒng)中定時同步對頻偏敏感以及整數(shù)倍頻偏估計實現(xiàn)復(fù)雜的問題,，本文在文獻[11]的基礎(chǔ)上,，提出了一種改進的訓(xùn)練序列結(jié)構(gòu)及時頻同步算法，仿真結(jié)果表明該同步算法具有良好的性能,。

1 OFDM系統(tǒng)模型

    OFDM基帶系統(tǒng)發(fā)射的時域信號可表示為：

2 改進的訓(xùn)練序列結(jié)構(gòu)和定時同步算法

2.1 改進的訓(xùn)練序列結(jié)構(gòu)

    由于文獻[11]的定時同步受頻偏影響,，同時小數(shù)頻偏估計范圍存在局限性，因此對訓(xùn)練序列結(jié)構(gòu)進行一定的改進,，采用如圖1所示的結(jié)構(gòu),。

    該結(jié)構(gòu)占用2個OFDM符號，由長度分別為N_c=N/2的c₁(n)和N的c₂(n)構(gòu)成,。CP和CS分別表示長度為N_g的循環(huán)前綴和循環(huán)后綴,。周期為N的ZC序列定義如下：

2.2 整數(shù)倍頻偏的影響

    整數(shù)倍頻偏不會破壞子載波分量的正交性，但是會對接收信號產(chǎn)生循環(huán)移位影響,，無法獲取正確的OFDM符號起始點,。在文獻[11]的整數(shù)倍頻偏影響分析的基礎(chǔ)上，以下針對本文改進的訓(xùn)練序列結(jié)構(gòu),，分析整數(shù)倍頻偏對定時峰值點的移位影響,。當(dāng)存在頻偏ε時，接收端接收到的信號y(n)與本地訓(xùn)練序列c₁(n)進行互相關(guān)如下：

    以上分析說明,，整數(shù)倍頻偏ε_I會使第一個訓(xùn)練序列c₁(n)的互相關(guān)峰值循環(huán)右移sε_I/2,，使第二個訓(xùn)練序列c₂(n)的互相關(guān)峰值循環(huán)左移sε_I。

2.3 改進的定時同步算法

    本文所提算法利用接收信號y(n)和本地的訓(xùn)練序列c₁(n)和c₂(n)進行互相關(guān)來獲取定時同步,，因此,，相應(yīng)的定時判決函數(shù)可表示為：

3 頻偏估計算法

    傳統(tǒng)的同步算法一般利用循環(huán)前綴進行頻偏估計，雖頻偏估計精度高,，但是估計范圍不大于0.5個子載波間隔,。為了彌補上述缺點，本文在得到準確的定時位置后,，利用第一個訓(xùn)練序列的重復(fù)性在時域完成小數(shù)頻偏粗估計：

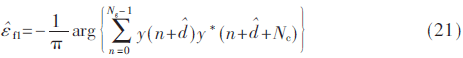
    式(21)中小數(shù)頻偏的估計范圍為[-1,，1]。用估計出來的小數(shù)倍粗頻偏估計對接收信號進行補償后,，剩余的小數(shù)倍頻偏絕對值小于0.5,。由于CS受到的多徑時延影響較小，因此利用此部分進行小數(shù)倍頻偏細估計：

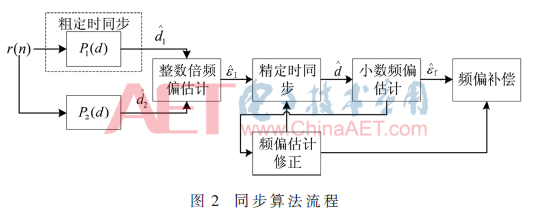
    綜合以上討論,，所提時頻同步算法流程可表示如圖2所示,。

4 仿真結(jié)果及分析

    為了驗證本文算法的有效性,，在高斯信道和多徑衰落信道下進行仿真，仿真次數(shù)為5 000次,，仿真參數(shù)如表1所示,。

    仿真中歸一化頻偏設(shè)置為ε=2.25和ε=3.75，根系數(shù)u設(shè)置為85,。多徑信道采用6徑的ITU車輛A(以下簡稱VA),，相對時延分別為[0，310,，710,，1090，1730,，2510](單位：ns),，平均功率分別為[0，-1,，-9,，-10，-15,，-20](單位：dB)。

    圖3和圖4分別給出了ε=2.25時定時偏移均方誤差(Mean Square Error of Symbol Timing Offset,，MSE of STO)和定時準確率的性能曲線,。在高斯信道下，當(dāng)信噪比(SNR)大于0 dB時,，文獻[6],、[8]、[11]和本文算法定時估計MSE都為零,，具有很高的定時準確率,，而在VA信道的影響下，文獻[5],、[6],、[8]、[11]的定時性能顯著下降;當(dāng)SNR<5 dB時,，文獻[11]的定時MSE低于文獻[4]～[6],、[8]，但是隨著信噪比的增大,，定時MSE基本保持不變,。同時,從圖4看出, VA信道下文獻[11]的定時準確率顯著下降, 這是因為該算法的定時性能很大程度依賴于頻偏估計性能，在多徑時延較大并附加頻偏時,，定時位置后移,使定時性能受到嚴重影響,。而本文算法在高斯信道和多徑信道下性能比較接近，且定時MSE始終是最低的，說明本文算法能有效地對抗多徑時延影響,，同步性能最優(yōu),。

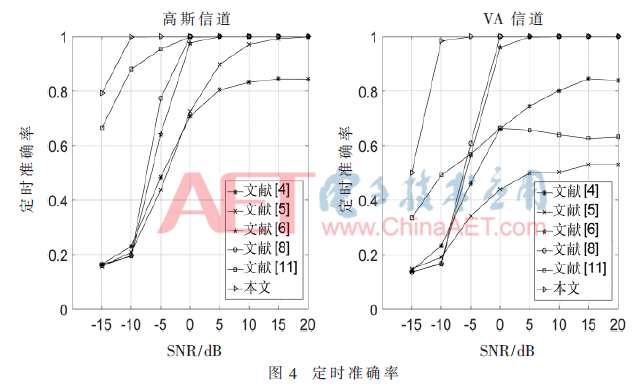
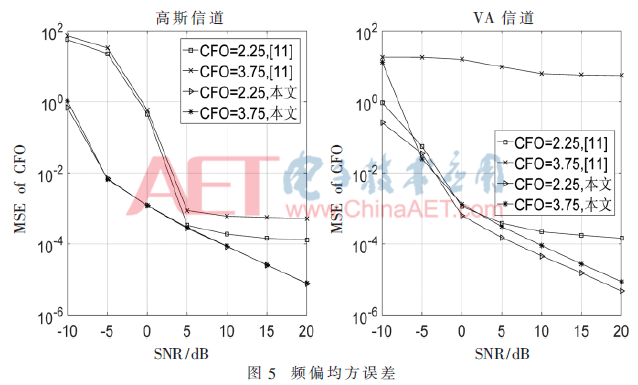
    圖5給出了頻偏均方誤差(Mean Square Error of Carrier Frequency Offset，MSE of CFO)的性能曲線,。在高斯信道以及低信噪比的情況下,，本文頻偏估計性能明顯優(yōu)于文獻[11]。從VA信道的性能曲線可以看出,，在頻偏為3.75的情況下,，文獻[11]始終保持較大的MSE,說明由于小數(shù)頻偏估計范圍的局限性，在多徑信道影響下,，當(dāng)小數(shù)倍頻偏大于0.5時,，頻偏估計性能會急劇惡化。此外,，無論整數(shù)倍頻偏取值為奇數(shù)或偶數(shù),，本文算法在兩種信道下均有較小的誤差，低于100數(shù)量級,，說明本文算法對頻偏估計范圍沒有局限性,，而且性能優(yōu)于文獻[11]算法。

5 結(jié)論

    本文在已有算法基礎(chǔ)上提出了一種改進的訓(xùn)練序列結(jié)構(gòu)和時頻同步算法,。相對于參考算法[11],，該算法利用改進的訓(xùn)練序列結(jié)構(gòu)擴大了同步算法的整數(shù)和小數(shù)頻偏估計范圍；同時定時不受頻偏的影響,，使定時同步性得到顯著提升,；而且定時后能在時域直接估計出整數(shù)倍頻偏，降低了算法復(fù)雜度,，簡化了系統(tǒng)同步過程,。此外，在定時同步之后進行小數(shù)頻偏估計,，提升了頻偏估計性能,。仿真結(jié)果表明，本文算法在多徑信道和頻偏影響的情況下,，能實現(xiàn)較為準確的定時同步和頻偏估計,。

參考文獻

[1] CUI T，ZHOU Q,，LI J,，et al.The analysis and research of adaptive transmission algorithms in wireless communication system[C].IEEE International Conference on Communication Problem-Solving(ICCP)，2015：615-618.

[2] HASSINE I B,，BOUALLEGUE R.Performances analysis of algebraic space time code under correlated and uncorrelated channels[C].International Conference on Advanced Communication Technology,，2014：262-268.

[3] VAN DE BEEK J J,，SANDELL M，BORJESSON P O.ML estimation of time and frequency offset in OFDM systems[J].IEEE Transactions on Signal Processing,，1997,，45(7)：1800-1805.

[4] SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transactions on Communications,，1997,，45(12)：1613-1621.

[5] MINN H，ZENG M,，BHARGAVA V K.On timing offset estimation for OFDM systems[J].IEEE Communications Letters,，2000，4(7)：242-244.

[6] PARK B,，CHEON H,，KANG C，et al.A novel timing estimation method for OFDM systems[J].IEEE Communications Letters,，2003,，7(5)：239-241.

[7] ZHOU E，HOU X,，ZHANG Z,，et al.A preamble structure and synchronization method based on central- symmetric sequence for OFDM systems[C].IEEE Vehicular Technology Conference，2008：1478-1482.

[8] Ren Guangliang,，Chang Yilin,，Zhang Hui，et al.Synchronization method based on a new constant envelop preamble for OFDM systems[J].IEEE Transactions on Broadcasting,，2005，51(1)：139-143.

[9] SHAO H,，LI Y,，TAN J，et al.Robust timing and frequency synchronization based on constant amplitude zero autocorrelation sequence for OFDM systems[C].2014 IEEE International Conference On Communication Problem-Solving(ICCP),，2014：14-17.

[10] 劉彬,，羅志年，彭疆.改進CAZAC序列的OFDM時域時頻同步算法[J].計算機工程與應(yīng)用,，2017,，53(14)：76-79.

[11] GUL M M U，Ma Xiaoli,，LEE S.Timing and frequency synchronization for OFDM downlink transmissions using zadoff-chu sequences[J].IEEE Transactions on Wireless Communication,，2015，14(3)：1716-1729.

[12] 王思撥,，馬社祥,，孟鑫,，等.基于訓(xùn)練序列的OFDM頻率同步改進算法[J].電子技術(shù)應(yīng)用，2017,，43(3)：104-107.

[13] WANG W J,，TIAN Y，AHN C J.Blind symbol timing synchronization scheme for real-time industrial wireless control network using high-speed preambleless OFDM systems over multipath fading channels[J].Digital Signal Processing,，2017,，62：30-37.

作者信息:

陳  穎，聶  偉

（北京化工大學(xué) 計算機系統(tǒng)與通信實驗中心,，北京100029）