文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.171373
中文引用格式: 張夢(mèng)影,曾成,狄素素,等. 多傳感器濾波融合的慣性定位算法[J].電子技術(shù)應(yīng)用,2017,43(10):86-88,98.
英文引用格式: Zhang Mengying,Zeng Cheng,Di Susu,et al. Inertial localization algorithm based on multi-sensor filter fusion[J].Application of Electronic Technique,2017,43(10):86-88,98.
0 引言
隨著以MEMS(Micro-electromechanical Systems)傳感器為代表的微型化慣性器件的發(fā)展,基于捷聯(lián)式慣導(dǎo)原理和MEMS傳感器的慣性定位技術(shù)也日益受到重視,特別是在難以接收衛(wèi)星信號(hào)的室內(nèi)、地下、礦井、水下、戰(zhàn)場(chǎng)等場(chǎng)合[1]。針對(duì)上述問(wèn)題往往采用利用電子羅盤(pán)對(duì)陀螺進(jìn)行校正的方法,在室內(nèi)、地下、礦井、水下等過(guò)程中磁強(qiáng)計(jì)更加容易受到干擾,造成方位更大的偏差。針對(duì)磁強(qiáng)計(jì)易受干擾和陀螺積分漂移的問(wèn)題已經(jīng)有眾多融合的算法出現(xiàn),比如卡爾曼濾波、無(wú)跡卡爾曼濾波(UKF)、擴(kuò)展卡爾曼濾波(EKF)等[2-4],這些濾波方法需要建立準(zhǔn)確的狀態(tài)方程和觀(guān)測(cè)方程。還有一種濾波算法是在互補(bǔ)濾波的基礎(chǔ)上進(jìn)行擴(kuò)展,比如經(jīng)典互補(bǔ)濾波、基于梯度下降法的互補(bǔ)濾波算法等[3-6],但是這種濾波算法適用的精度不高。面對(duì)這些問(wèn)題,本文提出了一種Kalman濾波和互補(bǔ)濾波融合的慣性定位算法,該算法在設(shè)計(jì)Kalman濾波中,將加速度計(jì)和磁強(qiáng)計(jì)融合得出的四元數(shù)作為觀(guān)測(cè)值,利用陀螺儀得出的四元數(shù)作為狀態(tài)值,通過(guò)數(shù)據(jù)的融合進(jìn)行濾波,完成四元數(shù)的第一次最優(yōu)估計(jì),針對(duì)陀螺漂移問(wèn)題則利用所設(shè)計(jì)的互補(bǔ)濾波對(duì)陀螺漂移進(jìn)行補(bǔ)償,得到校正后的角速度,進(jìn)而求得校正后不斷更新的四元數(shù),然后和第一次完成的最優(yōu)估計(jì)四元數(shù)通過(guò)第二次Kalman濾波進(jìn)行估計(jì),進(jìn)而輸出高精度的姿態(tài)角。
1 算法總體設(shè)計(jì)
Kalman濾波和互補(bǔ)濾波融合的慣性定位算法的總體思路如圖1所示。
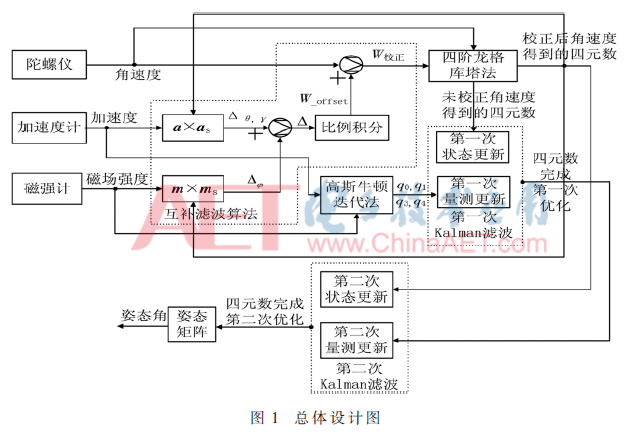
首先,將磁強(qiáng)計(jì)和加速度計(jì)測(cè)量的磁場(chǎng)強(qiáng)度和加速度利用高斯牛頓迭代法解算出的四元數(shù)送入Kalman濾波中當(dāng)作觀(guān)測(cè)值,將陀螺儀測(cè)量的角速度值利用四階-庫(kù)塔法解算出的四元數(shù)作為Kalman濾波的狀態(tài)值進(jìn)而得到四元數(shù)的第一次最優(yōu)估計(jì)值,在Kalman濾波過(guò)程中既可以去掉隨機(jī)噪聲,通過(guò)電子羅盤(pán)對(duì)陀螺儀進(jìn)行校正,又可以避免由于磁場(chǎng)干擾帶來(lái)的干擾數(shù)據(jù)。
其次,利用載體坐標(biāo)系和地理坐標(biāo)系之間的轉(zhuǎn)換矩陣,將地理坐標(biāo)系下的重力和地磁分量轉(zhuǎn)換到載體坐標(biāo)系下,然后與加速度計(jì)和磁強(qiáng)計(jì)在載體坐標(biāo)系下測(cè)量得到的加速度和磁場(chǎng)強(qiáng)度做向量積的運(yùn)算,將二者向量積的和相加經(jīng)過(guò)比例積分低通濾波,可以將電子羅盤(pán)測(cè)量姿態(tài)中的高頻抖動(dòng)信號(hào)濾出,然后和陀螺儀測(cè)量的角速度進(jìn)行融合,得到對(duì)陀螺儀補(bǔ)償后的角速度,利用四階龍格庫(kù)塔法得到校正后的四元數(shù)。
最后,將互補(bǔ)濾波算法得到的校正四元數(shù)作為狀態(tài)量,將第一次Kalman濾波得到的最優(yōu)四元數(shù)作為觀(guān)測(cè)量進(jìn)行第二次Kalman濾波,完成四元數(shù)的第二次優(yōu)化,然后通過(guò)四元數(shù)建立姿態(tài)矩陣求得更加精確的姿態(tài)角。
2 卡爾曼濾波設(shè)計(jì)
卡爾曼濾波(Kalman filtering)是一種利用線(xiàn)性系統(tǒng)狀態(tài)方程,通過(guò)系統(tǒng)輸入輸出觀(guān)測(cè)數(shù)據(jù),對(duì)系統(tǒng)狀態(tài)進(jìn)行最優(yōu)估計(jì)的算法。建立系統(tǒng)的狀態(tài)方程和測(cè)量方程是卡爾曼濾波的主要工作。本次卡爾曼濾波設(shè)計(jì)中用四元數(shù)的不斷更新量作為卡爾曼濾波中的狀態(tài)量。

下面建立測(cè)量方程,由重力加速度和三軸加速度計(jì)

式(4)中ax、ay、az表示重力加速度的測(cè)量值,重力加速度用g表示。
由地磁場(chǎng)和磁強(qiáng)計(jì)測(cè)量信息之間的關(guān)系可得:

由式(6)、式(7)并通過(guò)高斯牛頓迭代法求得四元數(shù),作為觀(guān)測(cè)量。觀(guān)測(cè)量取為:

式(8)中觀(guān)測(cè)量方程Z(k)=H(k)X(k)+V(k),其中H(k)為觀(guān)測(cè)量的增益矩陣,V(k)為觀(guān)測(cè)噪聲,方差R(k)可以通過(guò)傳感器的測(cè)量數(shù)據(jù)獲得。由于第一次Kalman濾波和第二次Kalman濾波都是對(duì)四元數(shù)的最優(yōu)估計(jì),故上述濾波公式和建立的方程均保持不變。
3 互補(bǔ)濾波算法設(shè)計(jì)
由于陀螺儀通過(guò)積分得到的方位角存在長(zhǎng)時(shí)間誤差積問(wèn)題,但其動(dòng)態(tài)響應(yīng)好,不易受外界干擾,而與之對(duì)應(yīng)的電子羅盤(pán)易受外界干擾,但它具有無(wú)誤差累積的優(yōu)點(diǎn)。互補(bǔ)濾波就是利用陀螺儀的高頻特性和電子羅盤(pán)的低頻特性進(jìn)行融合,通過(guò)比例環(huán)節(jié)進(jìn)行頻率特性的調(diào)節(jié),如圖2所示。
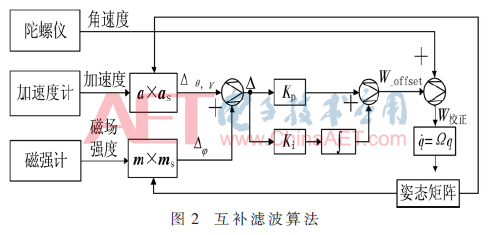
在圖2中,a、m表示載體坐標(biāo)系下加速度計(jì)和磁強(qiáng)計(jì)測(cè)量得到的加速度和磁場(chǎng)強(qiáng)度;將地理坐標(biāo)系下的重力分量和地磁分量通過(guò)四元數(shù)構(gòu)成的姿態(tài)轉(zhuǎn)換矩陣變換為載體坐標(biāo)系下的重力分量和地磁分量,分別用as和ms表示。在載體坐標(biāo)系下分別對(duì)a、as和m、ms做向量積的運(yùn)算,得到加速度計(jì)和磁強(qiáng)計(jì)對(duì)陀螺儀的校正誤差。其中俯仰角和橫滾角的誤差設(shè)為Δθ,γ,航偏角的誤差設(shè)為 即:
即:

將最后得到的角速度通過(guò)四階龍哥庫(kù)塔法進(jìn)行姿態(tài)解算,得到最優(yōu)姿態(tài)角。
4 實(shí)驗(yàn)驗(yàn)證和結(jié)果分析
本文采用MPU9150模塊進(jìn)行試驗(yàn)驗(yàn)證,通過(guò)硬件I2C總線(xiàn)的方式進(jìn)行數(shù)據(jù)的讀取,傳感器按100 Hz/s進(jìn)行數(shù)據(jù)更新,以外部中斷的方式進(jìn)行數(shù)據(jù)采集,然后將采集的數(shù)據(jù)存放于TF中,通過(guò)MATLAB編程進(jìn)行數(shù)據(jù)調(diào)用。為了驗(yàn)證此慣性定位融合算法的效果,主要在行走和磁場(chǎng)干擾嚴(yán)重的兩種模式下進(jìn)行測(cè)試,且兩種方式都是在室內(nèi)完成。圖3為攜帶傳感器人員(將傳感器綁在腳上)在室內(nèi)某一位置出發(fā),轉(zhuǎn)一圈回到起始位置,時(shí)長(zhǎng)約5 min;圖4為攜帶傳感器人員在下電梯過(guò)程中保持站立姿態(tài)的測(cè)試。在圖3和圖4中,單個(gè)陀螺儀解算(無(wú)濾波算法)用圖(a)代表,互補(bǔ)濾波算法用圖(b)代表,本算法用圖(c)表示。
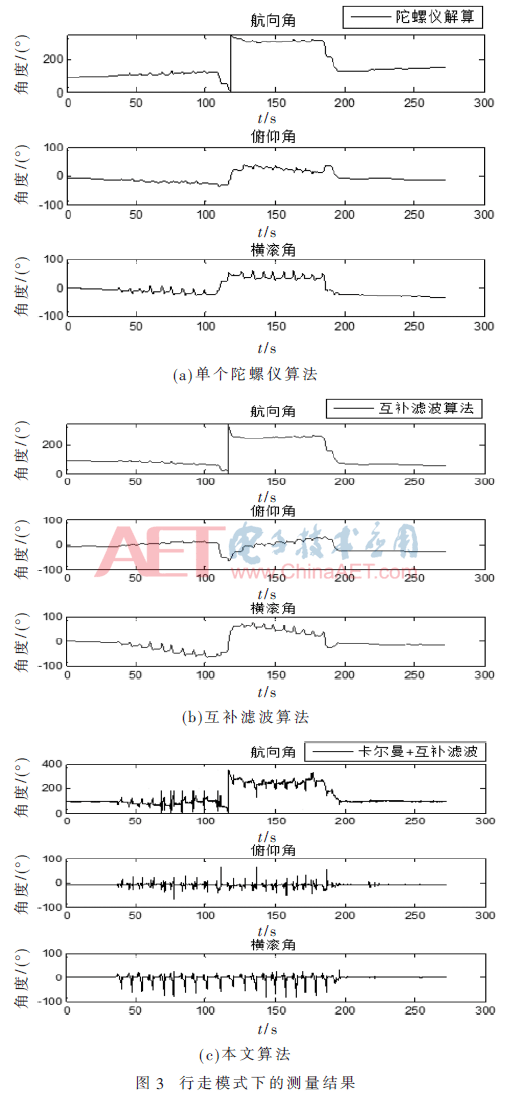
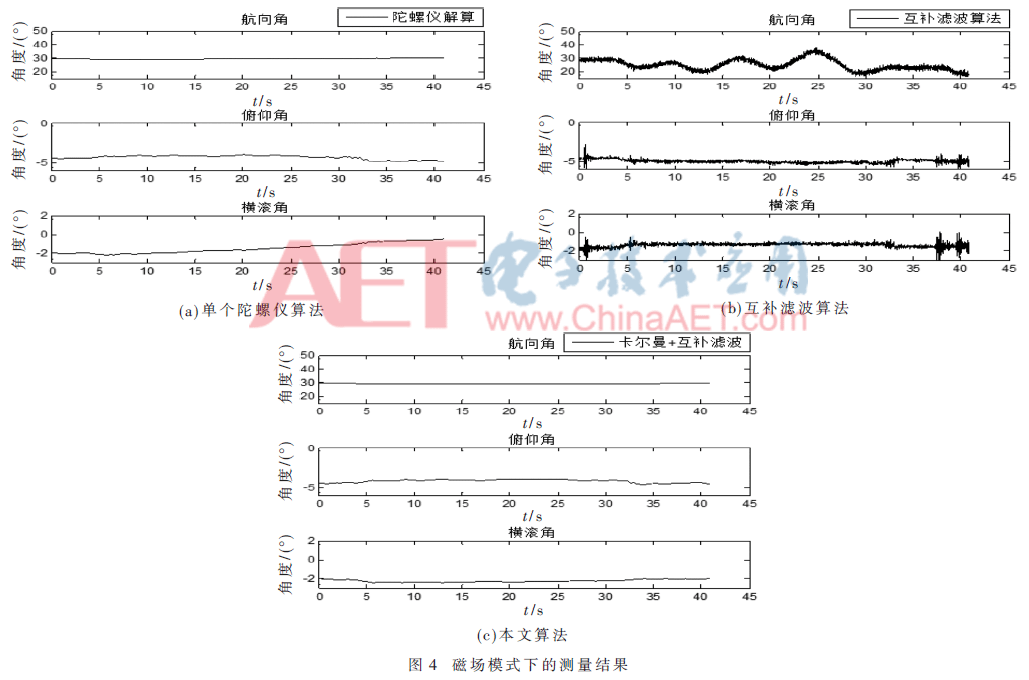
通過(guò)圖3對(duì)比始末位置方位偏差的數(shù)據(jù)結(jié)果可知,互補(bǔ)濾波算法雖然比單個(gè)陀螺進(jìn)行行人方位解算更加精確,但是利用互補(bǔ)濾波算法始末位置偏差在8°之內(nèi),而本算法在行走5 min左右始末位置偏差在 1.5°之內(nèi)。由圖3(c)證明本算法可以準(zhǔn)確提供在大動(dòng)態(tài)下(轉(zhuǎn)圈)的方位。由圖4可知,在電梯內(nèi)磁強(qiáng)計(jì)受到強(qiáng)烈干擾的情況下,僅利用互補(bǔ)濾波算法會(huì)比單個(gè)陀螺進(jìn)行解算出現(xiàn)更嚴(yán)重的方位偏差問(wèn)題,而利用Kalman濾波和互補(bǔ)濾波相融合的慣性定位算法避免了此問(wèn)題,確保姿態(tài)精度在2°以?xún)?nèi),有效抑制了磁場(chǎng)強(qiáng)度的干擾,確保方位的高精度輸出。
5 結(jié)束語(yǔ)
本文針對(duì)在導(dǎo)航解算中陀螺儀的積分偏差和磁強(qiáng)計(jì)容易受到干擾的問(wèn)題,提出了一種利用Kalman濾波和互補(bǔ)濾波相融合的慣性定位算法,利用Kalman濾波求最優(yōu)四元數(shù),利用互補(bǔ)濾波對(duì)陀螺儀的角速度進(jìn)行校正,通過(guò)校正的角速度進(jìn)行四元數(shù)的更新,將兩次校正后的四元數(shù)通過(guò)Kalman濾波求最優(yōu)四元數(shù)。通過(guò)實(shí)驗(yàn)結(jié)果可以看出,此方法不僅可以很好地解決陀螺漂移問(wèn)題,還能有效抑制磁強(qiáng)計(jì)受到干擾的問(wèn)題,能夠準(zhǔn)確地對(duì)方位進(jìn)行校準(zhǔn),實(shí)現(xiàn)姿態(tài)角高精度的穩(wěn)定輸出。
參考文獻(xiàn)
[1] 杜小菁,翟峻儀.基于MEMS的微型慣性導(dǎo)航技術(shù)綜述[J].飛航導(dǎo)彈,2014(9):77-81.
[2] 葉锃鋒,馮恩信.基于四元數(shù)和卡爾曼濾波的兩輪車(chē)姿態(tài)穩(wěn)定方法[J].傳感技術(shù)學(xué)報(bào),2012,25(4):524-528.
[3] MARINA H G,ESPINOSA F,SANTOS C.Adaptive UAV attitude estimation employing unscented Kalman filter,foam and low-cost MEMS sensors[J].Sensors,2012,12(7):9566.
[4] 張彤,孫玉國(guó).爾曼濾波在MEMS慣性姿態(tài)測(cè)量中的應(yīng)用[J].光學(xué)儀器,2015,37(1):28-30.
[5] 林偉捷,黃唯佳,蔡劍卿.基于四元數(shù)互補(bǔ)濾波和PID控制算法的兩輪自平衡車(chē)系統(tǒng)設(shè)計(jì)[J].軟件導(dǎo)刊,2016,15(6):80-82.
[6] KUNDRA L,EKLER P,CHARAF H.Orientation estimation in modern wearables with visual feature tracking[J].Journal on Multimodal User Interfaces,2015,9(4):313-322.
作者信息:
張夢(mèng)影,曾 成,狄素素,王云瑞
(河北工業(yè)大學(xué) 電子信息工程學(xué)院,天津300400)

