汪宋良

　?。▽幉ǔ鞘新殬I(yè)技術學院 信息學院,浙江 寧波 315100）

　　摘要：當均速管流量傳感器安裝在彎頭下游時,，由于流體流動為非充分發(fā)展湍流，增加了放大器流量檢測的誤差,。為提高儀表檢測精度,，提出了在超聲波氣體流量計前端一定距離安裝整流裝置改善氣態(tài)分布均勻性，減少超聲波測量誤差的方法,。采用理論計算分析和實際試驗相結合的方法,，基于傳統(tǒng)整流裝置，設計了改進型整流裝置結構,。經(jīng)實驗驗證,，安裝改進的裝置后，超聲波流量計的線性誤差減少到0.2%內,。

　　關鍵詞：超聲波技術,；氣體流量計；整流裝置,；流量測量,；測量誤差

　　中圖分類號：TH184文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.10.026

　　引用格式：汪宋良.提高超聲波氣體流量計精度的整流裝置研究［J］.微型機與應用，2017,36（10）：92-93,，95.

0引言

　　*基金項目：校內科研項目（ZZX16054）

　　為滿足氣體流量計測量不斷提高要求,，超聲波技術被應用于氣體流量檢測，它是繼孔板,、渦輪流量計之后出現(xiàn)的第三類高精度的新興氣體檢測儀表,。超聲波氣體流量計是通過超聲波脈沖沿順,、逆流兩個方向上聲傳播時間不同來測量氣體的流速和流量的新技術。由于它對流體無阻力,、無壓力損失,、受流體物理性質限制少以及使用簡單等特點，備受業(yè)界關注,，具有很大的前景,。換能器裝置及其關鍵技術、流場適應性問題,、時間測量技術等都將影響超聲波氣體流量計測量精度,。流場適應性問題又是相對容易解決的技術問題，它可以細分為管道走向,、管壁粗糙度,、阻流件及調整器等問題。

1流程適應性研究

　　對超聲波流量計流場適應性問題的研究主要分析管道走向,、調節(jié)裝置對流量檢測帶來的影響,，達到最適宜于流量計安裝及檢測的條件。管道走向的變化會改變流場速度分布并使之產生扭曲,，很多科研人員出于各種不同的目的都對這一現(xiàn)象進行過研究,，相關的研究成果近年來己被成功應用于氣體超聲波流量計。1982年,ENAYET M M等人利用激光多普勒技術對單彎管流場進行了分析［1］,。1991年,，LAI Y G等人利用理論推導與流體動力學相結合的分析方法計算了彎管中的流體擾動問題，對流場分布給出了數(shù)值解［2］,。1996年德國的科研人員HILGENSTOCK A和ERNST R將計算流體動力學與實驗技術相印證,，成功地分析了超聲波流量計檢測精度與彎管流場變形之間的關系［3］。1999年,，LIM K V等人探討了直角彎管中流場對電磁流量計檢測精度的影響情況,，他們的實驗測量數(shù)據(jù)最遠到達彎管后部22倍直徑的距離［4］。2015年,，吳春華［5］利用實驗測量系統(tǒng)測試了電路延時完成補償算法,，對多個標定流量點進行了樣機實流檢測，驗證了通過測量壓力差對彎管二次流誤差修正的流暢適應性仿真結果和補償方法的有效性,。2014年,，鄭丹丹等人基于實流實驗與數(shù)值仿真相結合［6］，對單聲道流量計的5種聲道布置進行研究,，表明聲道布置對流場適應性有一定的影響,。

　　綜合國內外學者對超聲波流量計復雜流場的研究成果，本文基于實流實驗和數(shù)值仿真相結合方法,，對流場整流裝置進行系統(tǒng)研究,，分別比較了多種不同的整流裝置對流場影響,，提出一種新型整流結構，最終實現(xiàn)整流效果,，提高超聲波流量計的流暢適應性,。

2新型整流裝置

　　由雷諾(Reynolds)實驗我們可以知道，流體在管道中流動時因為黏滯力的存在而產生兩種流態(tài)：層流與湍流,?？紤]到管道內流速分布的不均勻，一般會在管道內加裝整流器,，使流體通過整流器后,，流速分布狀況得到顯著改善。本設計主要針對超聲波氣體流量計管道內的整流器,，提出了一種包括整流器的開孔大小,、開孔個數(shù)、開孔位置等的設計方法,。

　　根據(jù)普朗特流速分布經(jīng)驗公式（式（1））可知,，在不同流體狀態(tài)下，流速分布是不同的,。

　　Vr=Vm(1－r2R2),，Re≤2 300，層流狀態(tài)

　　Vm(1－rR)1n,，Re≥4 000，湍流狀態(tài) （1）

　　式中,，Vr為流體距離軸芯線r處的沿軸線方向的面平均流速,；Vm為流體在軸芯線上的流速值（為Vr的最大值）；R為管道的半徑,；n為流速分布指數(shù),，它與管道內的流體雷諾數(shù)Re有關，如公式（2）所示,。

　　n=2lg(Ren)－0.8（2）

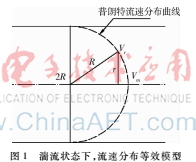
　　根據(jù)普朗特流速分布經(jīng)驗公式可以建立在湍流狀態(tài)下的流速分布等效模型,，如圖1所示。

　　假設流體處于湍流的臨界狀態(tài),，即Re=4 000,，此時根據(jù)公式（2）可以計算得到流速分布指數(shù)n=5；以管道軸芯線為豎坐標,，管道半徑為橫坐標,，建立轉換模型，如圖2所示,，豎坐標表示氣體流速,，橫坐標表示距離軸芯線的距離,。

　　首先確定整流器開孔位置及開孔個數(shù)，設計為由對稱環(huán)形分布的32個鉆孔組成,，孔的尺寸是管道內徑D的函數(shù),。(1)0.25D±0.002 5D節(jié)圓直徑上，一圈4個孔,；(2)0.50D±0.005 0D節(jié)圓直徑上,，一圈8個孔；(3)0.65D±0.006 5D節(jié)圓直徑上,，一圈4個孔,；(4)0.75D±0.007 5D節(jié)圓直徑上，一圈8個孔,；(5)0.85D±0.008 5D節(jié)圓直徑上,，一圈8個孔。然后確定各節(jié)圓直徑上開孔的直徑,，根據(jù)普朗特流速分布公式可以求得在各節(jié)圓直徑上的流速V1,、V2、V3,、V4,、V5，并求得位置與流速對應關系如圖2所示,。

　　加裝整流器的目的是使經(jīng)過整流后的流量分布均勻,，即通過整流器后的體積流量是均勻的，假設流過節(jié)圓直徑開孔的流速等于節(jié)圓直徑上的流速,，各節(jié)圓直徑上開孔的總面積分別為A1,、A2、A3,、A4,、A5，根據(jù)體積流量計算公式（3）,，流過各節(jié)圓直徑上開孔的體積流量相等,。

　　Q=VA（3）

　　式中：Q為體積流量，V為流體流速,，A為過流橫截面積,。

　　根據(jù)普朗特流速分布公式代入，可以得到公式（4）,。

　　A1=0.86A3

　　A2=0.93A3

　　A4=1.07A3

　　A5=1.19A3 （4）

　　由于整流器是安裝在管道內的,，因此開孔面積與管道橫截面積A有關。假設開孔總面積為1/2A，根據(jù)公式（4）計算得到A3=0.1A,。同理可以計算A1,、A2、A4,、A5與總面積A的關系,。

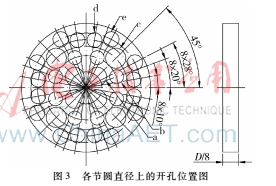
　　根據(jù)各節(jié)圓直徑上開孔個數(shù)以及圓的面積計算公式可以得到各節(jié)圓直徑上開孔的孔直徑分別表示為d1，d2,，d3,，d4，d5,分別等于0.147D,，0.108D,，0.158D，0.116D,，0.122D,。確定好各節(jié)圓直徑上開孔數(shù)目以及開孔直徑后，需要確定開孔在節(jié)圓直徑上的開孔位置,，根據(jù)機械結構的特性,，開孔位置如圖3所示。

3實驗結果

　　本實驗測量模型如下：

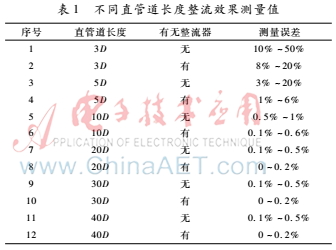
　?。?）測量管道模型直徑D固定,；（2）氣體經(jīng)過彎道形狀固定，到達下游測試前直管道（整流裝置安裝在直管道的最前端）距離長短不同,，分別為3D,、5D、10D,、20D,、30D、40D,；（3）測量區(qū)管段（安裝超聲波測量聲道的管道長度）長度固定；（4）經(jīng)過測量區(qū)后的氣態(tài)出口緩沖區(qū)管道長度固定為20D,。具體測試數(shù)據(jù)如表1所示,。

　　以上實驗數(shù)據(jù)說明：（1）比較上述6個距離處測量值可以看出，當測量表體安裝在距離出口10D管徑之后時,，其流場分布區(qū)域平穩(wěn),；（2）將其與無整流器的情況進行比較，發(fā)現(xiàn)其流線延軸向的旋轉速率變緩,，而且速度較為均衡的區(qū)域變多,；（3）通過自行設計的整流裝置效果對比，發(fā)現(xiàn)整流裝置對管道紊流氣態(tài)有非常大的穩(wěn)定作用，大大提升了儀表測量精度,。

4結論

　　本文通過理論計算實現(xiàn)了一種氣體流量計的整流裝置,，實驗數(shù)據(jù)表明該裝置能有效提高氣態(tài)平均分布，提高儀表測量精度,。

參考文獻

　?。?］ 溫靜馨, 郝建秀, 王淮中. 新型超聲波氣體流量計［J］. 微型機與應用,2010,29(9):25-27.

　　［2］ LAI Y G, SO R M C, ZHANG H S. Turbulencedriven secondary flows in a curved pipe［J］.Theoretical and Computational Fluid Dynamics, 1991,3(3):163-180.

　?。?］ HILGENSTOCK A, ERNST R. Analysis of installation effects by means of computational fluid dynamicsCFD vs experiments?［J］. Flow Measurement and Instrumentation, 1996, 7(3):161-171.

　?。?］ LIM K W, CHUNG M K. Numerical investigation on the installation effects of electromagnetic flowmeter downstream of a 900 elbowlaminar flow case［J］. Flow Measurement and Instrumentation, 1999(10):167-174.

　　［5］ 胡春華. 時差法超聲波流量計的研制及流暢適應性研究［D］.杭州:浙江理工大學,2015.

　?。?］ 鄭丹丹. 單聲道超聲波流量計不同聲道布置形式的流場適應性［J］.天津大學學報,2014,47(8):703-710.