文獻(xiàn)標(biāo)識碼: A
DOI:10.16157/j.issn.0258-7998.2015.10.011
中文引用格式: 杜微,李榮寬. 一種分步式Dual slope ADC的研究與設(shè)計[J].電子技術(shù)應(yīng)用,2015,41(10):45-48.
英文引用格式: Du Wei,Li Rongkuan. Design of a new subranged dual slope A/D converter [J].Application of Electronic Technique,2015,41(10):45-48.
0 引言
溫度、壓力等緩慢變化的信號一般頻率很低(幾赫茲甚至更低),當(dāng)傳感器在感受這些緩慢變化的信號之后,需要通過一個轉(zhuǎn)換速率可以很低但必須很精準(zhǔn)的模數(shù)轉(zhuǎn)換器將未知的模擬信號轉(zhuǎn)換為已知的數(shù)字信號[1]。雙積分 ADC 應(yīng)用非常廣泛。傳統(tǒng)的結(jié)構(gòu)主要由1個帶有輸入切換開關(guān)的模擬積分器1個比較器和1個計數(shù)單元構(gòu)成,通過兩次積分將輸入的模擬電壓轉(zhuǎn)換成與其平均值成正比的時間間隔。與此同時,在此時間間隔內(nèi)利用計數(shù)器對時鐘脈沖進(jìn)行計數(shù),從而實現(xiàn)模數(shù)轉(zhuǎn)換。積分型 ADC 兩次積分的時間都是利用同一個時鐘發(fā)生器和計數(shù)器來確定,因此所得到的表達(dá)式與時鐘頻率無關(guān),其轉(zhuǎn)換精度只取決于參考電壓[2]。此外,由于輸入端采用了積分器,所以對交流噪聲的干擾有很強的抑制能力:能夠抑制高頻噪聲和固定的低頻干擾(如50 Hz或60 Hz),適合在嘈雜的工業(yè)環(huán)境中使用[3]。這類ADC 分辨率高,傳統(tǒng)結(jié)構(gòu)可達(dá)到22位,還具有功耗低、成本低等特點。大量應(yīng)用于低速、精密測量等領(lǐng)域,如現(xiàn)有工業(yè)、民用儀器儀表中。
1 基本原理
此新型Dual slope ADC的實質(zhì)是基于分步式ADC的轉(zhuǎn)換原理,一個基本的m+n位的奈奎斯特ADC的轉(zhuǎn)換過程可以用數(shù)學(xué)公式表示為:

由式(2)可以看出此m+n位ADC的轉(zhuǎn)換公式可以拆分成兩個A/D轉(zhuǎn)換公式,一個n位ADC的轉(zhuǎn)換公式為:
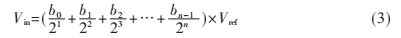
其中的Vin是系統(tǒng)輸入的未知模擬電壓,Vref是給定的參考電壓。另一個m位子ADC的轉(zhuǎn)換公式為:
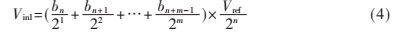
其中,Vin1為未知的輸入信號,而此m位ADC的參考電壓為:

至此,從理論推導(dǎo)的角度證明了這種分步式ADC結(jié)構(gòu)的合理性。
此分步式ADC先進(jìn)行n位ADC的轉(zhuǎn)換,將轉(zhuǎn)換完成后的剩余電壓作為m位子ADC的未知輸入信號。整個過程等效實現(xiàn)了m+n位ADC的轉(zhuǎn)換。但前n位ADC轉(zhuǎn)換的剩余電壓比較小,比較器可能無法分辨[3]。為了解決了這個問題,本系統(tǒng)中引入了自動補償電路,如圖1所示,通過開關(guān)控制積分器電阻和電容的比值,從而改變積分的時間常數(shù)。使得比較器的輸入信號幅度不會被衰減。
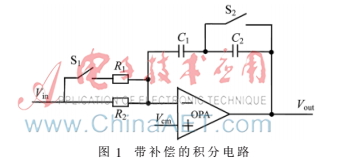
此自動補償方法不會影響分步式Dual slope ADC轉(zhuǎn)換的精準(zhǔn)性,系統(tǒng)中帶補償?shù)姆e分電路如圖1所示,正反向積分轉(zhuǎn)換過程如圖2所示。正向積分時系統(tǒng)的輸入為未知的模擬信號Vin,而反向積分時系統(tǒng)的輸入為參考電壓Vref。

由虛短路、虛斷路原則可以得到:
![3O[]VIIZZFRGH`JU1YA0~}H.png 3O[]VIIZZFRGH`JU1YA0~}H.png](http://files.chinaaet.com/images/2017/01/12/6361981439148053854172852.png)
式中的Vcm為運算放大器的共模電壓,此系統(tǒng)中為2.5 V。Req、Ceq為補償后的等效電阻和電容,這兩個值由開關(guān)控制,可以得出輸出電壓為:

由圖2可知,在T1=2nTck時積分器的輸出電壓為:
![16]@6T7{{OPR~QTOHCTDVLW.png 16]@6T7{{OPR~QTOHCTDVLW.png](http://files.chinaaet.com/images/2017/01/12/6361981457783053851864909.png)
反積分過程接入的電壓為Vref,從T1時刻積分到T1+T2時刻的輸出電壓為:
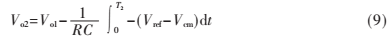
當(dāng)Vo2=0時比較器剛好翻轉(zhuǎn),此時由式(8)、式(9)可以得到轉(zhuǎn)換關(guān)系式:

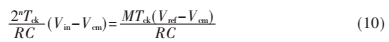
其中的MTck=T2為反積分的時間,輸入的未知模擬電壓為:
![E9_AQ$~Y~`K@]7U(4JUMYM9.png E9_AQ$~Y~`K@]7U(4JUMYM9.png](http://files.chinaaet.com/images/2017/01/12/6361981641933953859774930.png)
由式(10)、式(11)的表達(dá)式可以看出最終的所求電壓Vin與積分時間常數(shù)RC沒有關(guān)系,只要保證正反向積分的時間常數(shù)相同,那么此Dual slope ADC的轉(zhuǎn)換精度就不會受到影響[4]。而此系統(tǒng)中的補償方法滿足穩(wěn)定條件,所以這種補償方法是可行的。
2 系統(tǒng)結(jié)構(gòu)
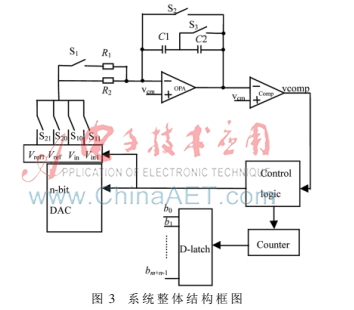
基于以上原理,文中所設(shè)計的分步式Dual slope A/D轉(zhuǎn)換器由補償積分器、比較器、D/A轉(zhuǎn)換器(DAC)、數(shù)字控制邏輯等幾部分組成,如圖3所示。Vref為n位ADC的輸入?yún)⒖茧妷海琕in1是n位ADC轉(zhuǎn)換完成后的剩余電壓(也是m位ADC的未知輸入電壓),Vref1為m位ADC參考電壓。其中Vin1、Vref1可以通過數(shù)字邏輯控制n位DAC模塊而獲得。
整個m+n位ADC的轉(zhuǎn)換分為兩個過程,當(dāng)S10、S20閉合,S1、S2、S3、S11、S21斷開時為n位ADC的轉(zhuǎn)換過程,此時未知輸入信號Vin及參考電壓Vref通過開關(guān)S10、S20接入電路,此過程與傳統(tǒng)的雙積分ADC的工作過程相同。轉(zhuǎn)換完成后,通過鎖存器將得到的n位ADC的轉(zhuǎn)換結(jié)果存儲起來。當(dāng)開關(guān)S10、S20、S2斷開,S11、S21、S1、S3閉合時為m位ADC的轉(zhuǎn)換過程,此時未知輸入信號Vin1及參考電壓Vref1通過開關(guān)S11、S21接入電路。進(jìn)行m位ADC的轉(zhuǎn)換過程。整個過程實現(xiàn)了m+n位ADC的轉(zhuǎn)換。
此結(jié)構(gòu)相對于傳統(tǒng)的雙積分ADC的創(chuàng)新之處有:
(1)通過開關(guān)S10、S20、S11、S21控制實現(xiàn)兩步轉(zhuǎn)換的過程。
(2)通過開關(guān)S1、S3實現(xiàn)了自動補償?shù)墓δ埽WC了m位子ADC轉(zhuǎn)換的精準(zhǔn)性。
(3)通過增加一個DAC電路將n位ADC轉(zhuǎn)換的剩余電壓提取出來,進(jìn)行m位子ADC的轉(zhuǎn)換,從而具備了再分辨的能力。
3 電路設(shè)計

系統(tǒng)中的DAC結(jié)構(gòu)如圖4所示,其中C是單位電容,最右端的電容為終端匹配電容。第一個時鐘周期為放電過程,此時k1、k2為高電平,d1、b1~b10全部為低電平。第二個時鐘周期為采樣過程,此時k1、k2、d1、b1~b10全部為高電平。緊接著的十個時鐘周期是轉(zhuǎn)換過程,此時k1、d1是低電平,b1~b10受數(shù)字控制邏輯控制[5]。其余的時鐘周期為n位ADC轉(zhuǎn)換的剩余電壓提取過程,此時k1為高電平,k2、b1~b10全部為低電平。
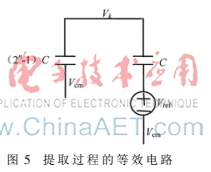
由DAC的轉(zhuǎn)換過程,可以得到簡化的等效電路如圖5所示,從此等效電路可以容易地提取出所需要的電壓Vin1、Vref1。
由基本的電容串聯(lián)分壓理論求得:

DAC電容陣列的上下極板的電荷守恒可以得到:
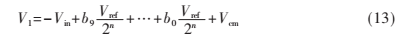
而電壓Vk正好就是參考電壓Vref1,電壓V1就是Vin1。
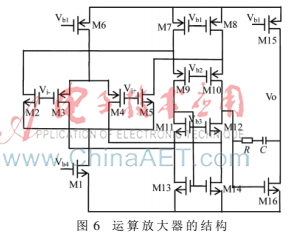
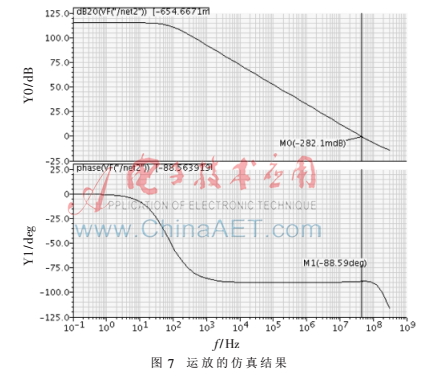
系統(tǒng)中的運放采用折疊共源共柵結(jié)構(gòu),為了增大輸入共模范圍而采用軌到軌運放的結(jié)構(gòu)[6],具體實現(xiàn)電路如圖6所示。在0.5 m工藝下,對此運放進(jìn)行仿真,其增益和相位曲線如圖7所示,由圖可知運放的增益達(dá)到118 dB,相位裕度大于80°,單位增益帶寬達(dá)到100 MHz。
4 系統(tǒng)仿真結(jié)果
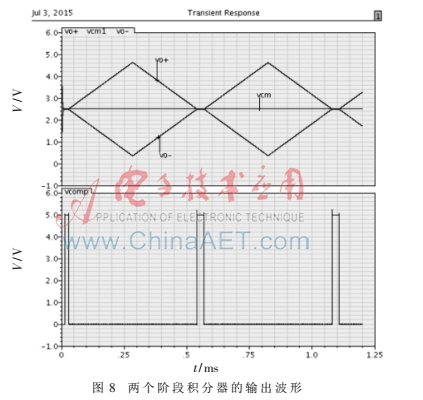
用Cadence軟件對搭建的系統(tǒng)進(jìn)行瞬態(tài)仿真,整個過程積分器的輸出波形如圖8所示,電壓Vo+表示16位ADC的輸出。可以看到由于采用了自動補償電路,使得整個ADC的積分器輸出幅度不會衰減。

在系統(tǒng)時鐘頻率為1 MHz,輸入信號頻率為0.5 kHz時,16位(m=n=8)ADC的系統(tǒng)轉(zhuǎn)換結(jié)果如圖9所示,當(dāng)輸入電壓為3.0 V時,n位ADC的轉(zhuǎn)換結(jié)果約為2.992 2 V,而m+n位ADC的轉(zhuǎn)換結(jié)果約為2.999 92 V。有效位數(shù)大約為15位,其中的誤差主要來自于數(shù)字控制邏輯,若繼續(xù)對控制邏輯進(jìn)行優(yōu)化,分步式Dual slope ADC結(jié)構(gòu)可以很容易達(dá)到很高的精度,同時速度也會得到提高。
相對于傳統(tǒng)的雙積分ADC,此分步式Dual slope ADC結(jié)構(gòu)具有以下優(yōu)點:
(1)此系統(tǒng)具有自動補償功能,可以自動調(diào)節(jié)電壓幅度,從而達(dá)到更高的分辨率。而且減小了傳統(tǒng)雙積分ADC對大電容的依賴性。
(2)此系統(tǒng)的兩個過程通過復(fù)用的方式實現(xiàn),從而使得芯片的功耗不會明顯增大。
(3)此結(jié)構(gòu)采用了分段結(jié)構(gòu),會將傳統(tǒng)的雙積分ADC的轉(zhuǎn)換時間提高很多,傳統(tǒng)結(jié)構(gòu)最慢的轉(zhuǎn)換需要22n個時鐘周期,而此結(jié)構(gòu)只需要2n個時鐘周期。
5 結(jié)論
此新型Dual slope ADC系統(tǒng)采用了分步式工作方式,不僅會使其分辨率較傳統(tǒng)的雙積分ADC得以提高,而且轉(zhuǎn)換速率也會大幅度提升;同時還引入了自動補償方法,從根本上改善了傳統(tǒng)的雙積分ADC需要大的分布電容的缺點。值得一提的是:此系統(tǒng)由于采用了復(fù)用技術(shù),所以將會和傳統(tǒng)的雙積分ADC一樣具有低功耗的優(yōu)勢。此系統(tǒng)的缺點是數(shù)字控制邏輯比傳統(tǒng)方法更復(fù)雜,且占據(jù)的芯片面積要有所增加,所以如何找到一種簡潔有效的控制方法至關(guān)重要。此系統(tǒng)結(jié)構(gòu)將更加適合于在低速、精密測量等領(lǐng)域應(yīng)用。
參考文獻(xiàn)
[1] RAZAVI B.模擬CMOS集成電路設(shè)計[M].陳貴燦,等,譯.西安:西安交通大學(xué)出版社,2001.
[2] ALLEN P E,HOLBERG D R.CMOS analog circuit design[M].Second edition.Oxford University.Inc,ISBN 0-19-511644-5,2002.
[3] JOHNS D A,MARTIN K.Analog integrated circuit design[M].New York:iley,1997.
[4] BAKER R J.CMOS circuit design,layout and simulation[M].3rd Edition,John Wiley & Sons,2010.
[5] 羅剛.基于雙積分原理的ADC設(shè)計[D],成都:電子科技大學(xué),2009.
[6] 趙天挺.一種CMOS 12-bit 125ksps全差分SAR ADC[D].天津:南開大學(xué),2004.

