馬迎輝,，彭成，張文佳,，滿君豐

　　(湖南工業(yè)大學 計算機與通信學院,湖南 株洲 412000)

　　摘要：隨著網(wǎng)絡化軟件應用領域的逐步擴大,，軟件業(yè)對軟件的安全性、可靠性提出了更高的要求,。軟件一旦出現(xiàn)故障,，會給人們的生活、工作帶來不便,，甚至造成嚴重的危害,。因此，研究故障在網(wǎng)絡化軟件中引起的異常行為迫在眉睫,。依據(jù)復雜網(wǎng)絡上的SIR模型,，對網(wǎng)絡化軟件中異常行為的傳播過程進行了理論分析和數(shù)值模擬，表明了復雜網(wǎng)絡特性對異常行為傳播的重要影響,。

　　關鍵詞：網(wǎng)絡化軟件,；復雜網(wǎng)絡；軟件故障,；異常行為

0引言

　　軟件復雜性的增加直接導致軟件故障的增加,。軟件發(fā)生故障或者異常是由于一些內(nèi)外部的因素，致使軟件中類,、方法,、函數(shù)等出現(xiàn)錯誤,，不能夠完成軟件應有的功能。如果一個或者多個個體發(fā)生故障,，那么這個故障就會隨著調(diào)用和依附關系傳播到其他的個體甚至導致整個系統(tǒng)無法正常運行,，最終導致整個系統(tǒng)的崩潰。這種使系統(tǒng)失效的行為被稱為異常行為,。目前,，各種因素都在引領著軟件技術的重大改革，軟件的形態(tài)也明顯呈現(xiàn)出網(wǎng)絡化趨勢,，隨著復雜網(wǎng)絡技術,、服務技術的迅速發(fā)展，網(wǎng)絡化軟件［1］已然成為了現(xiàn)代軟件系統(tǒng)的主要形態(tài),?？偟膩碚f，網(wǎng)絡化軟件就是以因特網(wǎng)為載體,、以互聯(lián)網(wǎng)上的各種資源信息為元素,、以各個元素之間的相互協(xié)同和互操作為構造手段、行為與拓撲結構能夠動態(tài)演變的密集型混合軟件系統(tǒng)［2］,。另外,，網(wǎng)絡化軟件系統(tǒng)不但組成元素間的交互、代碼數(shù)量比較龐大,，而且數(shù)據(jù)訪問,、存取規(guī)模和硬件設備也大大超過了傳統(tǒng)的軟件。規(guī)模和數(shù)量在各維度上大規(guī)模增加,，這不僅使得對軟件系統(tǒng)的理解和改造難度增加,，而且也使得軟件故障對系統(tǒng)的破壞能力更加嚴重［3］，因此,，研究網(wǎng)絡化軟件系統(tǒng)中異常行為的傳播迫在眉睫,，以期在軟件系統(tǒng)崩潰前能夠得到有效的控制，從而維持系統(tǒng)安全有效地運行,。

　　目前,，研究網(wǎng)絡動力學主要是依據(jù)病毒傳播的行為，近來也取得了很大的發(fā)展,。另外,，研究病毒傳播最廣泛的模型是SIS模型［45］與SIR模型［6］，而無標度網(wǎng)絡［78］則是使用最多的網(wǎng)絡模型,。在復雜網(wǎng)絡［9］里,，每個單位節(jié)點代表一個單獨的個體，任意選取其中的一個節(jié)點作為感染源，節(jié)點與節(jié)點之間的連線代表病毒的傳播路徑,。在小世界網(wǎng)絡［1011］中廣泛使用的是SIS模型,，并且，其和SIR模型主要關注的是感染幾率閾值的問題,。

　　鑒于此,，本文依據(jù)復雜網(wǎng)絡中對病毒傳播行為的研究，利用SIR模型,，對網(wǎng)絡化軟件系統(tǒng)中的異常行為傳播過程進行理論分析和數(shù)值模擬，并對影響病毒傳播的因素的感染幾率,、度分布,、集聚系數(shù)等參數(shù)進行分析比較，得出這些參數(shù)對網(wǎng)絡化軟件系統(tǒng)中異常行為傳播的影響具有相同的效果,。研究異常行為的傳播可以為異常行為的控制提供有意義的指導,。對異常行為的研究是十分有價值的。

1相關工作

　　軟件異常作為影響軟件正常運行的重要因素,，它的一些相關研究引起了研究人員的廣泛關注,。由于人為的原因，故障在很多人工復雜系統(tǒng)中都有出現(xiàn),。很多領域都有對故障的研究,，例如通信網(wǎng)絡故障、電路故障,、電力系統(tǒng)故障等,，提出了許多研究成果和技術。

　　現(xiàn)階段一些相關人員主要基于軟件的靜態(tài)拓撲圖,，從各個層次對軟件故障進行研究,。王建等［12］利用軟件中函數(shù)間的交互關系，通過模型的建立去模擬軟件的故障傳播,，進而研究軟件中存在的級聯(lián)故障,。最后，通過對現(xiàn)實中軟件進行模擬實驗,，分析了影響級聯(lián)故障傳播的因素,，并研討了形成這些影響的原因。周寬久等［13］人通過對軟件執(zhí)行路徑的提取,，建立軟件的加權網(wǎng)絡,，利用耦合映像格子（Coupled MapLattice，CML）模型［14］,，研究大型軟件系統(tǒng)故障的傳播過程,，并且在此基礎上提出了一種依據(jù)關鍵路徑進行軟件測試的方法。Damien Challet,，Andrea Lombardoni等［15］人在Linux系統(tǒng)環(huán)境下,，基于各個軟件包間的相互依存關系,，對單一故障進行討論分析。Mohamed A與Zulkernine M等人也是在組件級別對軟件故障傳播及其對軟件可靠性的影響進行了討論分析,，同時也提出了一種基于架構服務路徑（Architectural Service Routes,，ASR）的軟件故障傳播技術，并且分析確認了故障在構建中傳播的下限與上限,，最后得出架構與系統(tǒng)可靠性間的聯(lián)系,。

2網(wǎng)絡化軟件異常傳播理論分析

　　可以把網(wǎng)絡化軟件系統(tǒng)作為一個復雜的網(wǎng)絡，假設這個復雜的網(wǎng)中有n個節(jié)點,，首先選擇其中一個作為感染個體（I）,，若異常則沿著節(jié)點間的連線進行傳播，假定感染個體（I）只能將異常傳播到其鄰居節(jié)點,。設鄰居節(jié)點被傳播感染的概率為φ,，感染個體（I）轉化為免疫個體（R）的概率為τ。假定τ=1,，意思就是說感染個體只能維持一個時間步長,。

　　這里用I（t）表示網(wǎng)絡里被感染個體的總數(shù)。一段時間后,，感染節(jié)點（I）離感染源越來越遠,，被感染的節(jié)點數(shù)目逐漸增多。在有限的時間里,，I（t）逐漸減少,，當I（t）最終等于零時，則異常傳播過程結束,。由此可知,，φ越大，傳播的時間越長,，被感染個體也越多,；當φ=1時，網(wǎng)絡中的所有節(jié)點都會被感染,。

　　依據(jù)擴散定義,，可以得出異常傳播的公式：

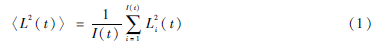
　　其中，Li(t)表示每個感染節(jié)點到感染源的最短距離,。

　　正如前面所說,，網(wǎng)絡中的三角結構與環(huán)形結構會對異常行為傳播造成影響。下面用圖1所示同心圓來證明,。

　　圖1中,，圓心表示異常源點，最內(nèi)層上的節(jié)點與圓心的間距Li(t)=1，第二層上的節(jié)點與圓心的距離Li(t)=2,，依次類推,。當不同層之間有連接時，某層上的異常個體就可能傳播到同層或者是比其更低的一層,，第二層上的異常點就有可能傳播到同層,、第一層或者第三層上的個體，不過前兩種情況會使得〈L2(t)〉=tη中的η小于2,。所以,，網(wǎng)絡化軟件的復雜網(wǎng)絡結構就決定了異常傳播指數(shù)η的大小。

　　一般而言,，描述網(wǎng)絡結構比較重要的兩個參數(shù)是集聚系數(shù)C和度分布P（k）,。前者表示某個節(jié)點的兩個鄰居節(jié)點仍為鄰居的可能性，后者表示網(wǎng)絡中度相同的所有節(jié)點的密度,。集聚系數(shù)越大表明網(wǎng)絡中的三角結構越多。下面就研究這兩個參數(shù)對異常傳播指數(shù)η的影響,。

　　在某一時刻t,，感染個體具有不同的Li(t)。假設Li(t)以δ1(t)的概率取t值,，Li(t)以δ2(t)的概率取t－1,，…，Li(t)以δt(t)的概率取1,。那么〈L2(t)〉可表示為：

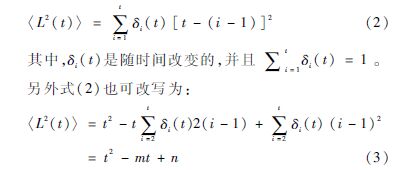
　　假定式（3）可寫為：

　　〈L2(t)〉～tX（4）

　　在異常傳播過程中,，δi(t)是由節(jié)點感染概率φ、集聚系數(shù)C與度分布P(k)共同決定的,。這里只討論網(wǎng)絡結構對傳播指數(shù)的影響,，因此假設φ為定值。集聚系數(shù)C的值越大,，表明網(wǎng)絡中的三角結構越多,，異常傳播的幾率就很小。因此,，η的值隨C增大而減小,。而對于度分布P(k)，假如網(wǎng)絡為BA無標度網(wǎng)絡,，那么對于度大的節(jié)點而言,，則很容易被感染，并會將此異常傳播給其他更多節(jié)點,。假如網(wǎng)絡為小世界網(wǎng)絡,，那么異常的傳播是循序漸進的，被感染的節(jié)點相對來說比較少。如果把異常行為傳播的過程分為兩個部分,，一個是直接向前傳播,，另一個是三角形路線傳播。沿三角形傳播又可分為向前和向后兩種,，并且概率相同,。綜上所述，在網(wǎng)絡化軟件中異常行為傳播指數(shù)η是大于1的,。

3實驗分析

　　下面通過數(shù)值模擬來驗證上述結論,，本文中選用WS小世界網(wǎng)絡模型和HK模型。兩個模型中,，都可以調(diào)節(jié)一定的參數(shù)來改變集聚系數(shù)C的大小,。另外，對于固定不變的集聚系數(shù)C,，WS模型與HK模型的度分布P(k)不同,。所以，用這兩個模型來研究度分布P(k)和集聚系數(shù)C對傳播指數(shù)的影響,。

　　對于WS小世界模型,，其最初是一個具有N個節(jié)點的一維鏈，其中的各個節(jié)點與附近的X個節(jié)點相連,，接著以概率ω斷開并重新相連,，但是新連接的節(jié)點從網(wǎng)絡中的其他節(jié)點中隨機選擇，避免自連接與重復連接,。然后,，在小世界網(wǎng)中隨機選取一個節(jié)點作為異常源點，讓此異常源點以φ的感染概率進行傳播,。最終,，得出〈L2(t)〉與t的關系隨ω與X的變化而變化。

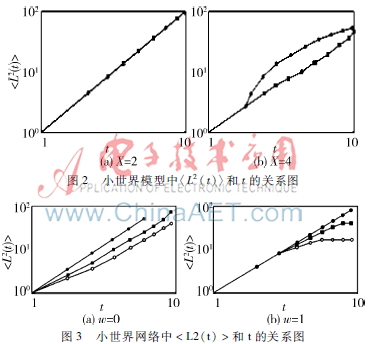
　　圖2中,，圓圈和正方形分別表示ω=0,，1。從圖2（a）中可以看出,，對于ω=0和1,，兩條直線是重合的，η=2,。而在圖2（b）中,，兩條線開始分離，只有ω=1這條線接近于<L2(t)>=t2,。這主要是因為當ω=1時,，網(wǎng)絡成為隨機網(wǎng)絡,，其集聚系數(shù)比較小，從而使η接近2,。當1<ω<2時,，網(wǎng)絡有了一定的集聚系數(shù)，η也就偏離了2,。

　　圖3中,，實心圓、正方形,、空心圓分別代表K=2,、4、6,。

　　圖2小世界模型中〈L2(t)〉和t的關系圖

　　圖3小世界網(wǎng)絡中<L2(t)>和t的關系圖

　　傳播是由δi(t)決定的,，并且δi(t)是隨著時間而變化的。也就是說δi(t)的分布情況決定著η值的大小,。下面對δi(t)和t的關系進行數(shù)據(jù)分析,。圖4中上圖顯示了在不同ω值的情況下δ1(t)和t之間的聯(lián)系。圖中顯示,，在最初的5個時間段里,，隨著ω的增大，δ1(t)的減小速度變慢,，意思是當ω取最大值時,，δ1(t)也最大,。除了δ1(t),，同樣分析了δi(t)的分布情況，結果如圖4中下圖所示,，可以看出δ1(t)與-mt+b的分布趨勢是一樣的,。

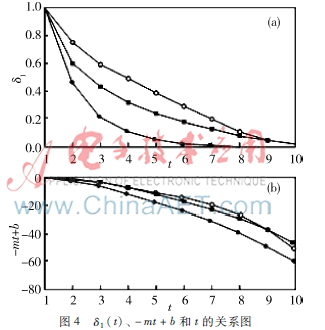
　　接下來，具體可按照以下步驟來構造HK模型：(1)起始狀態(tài),，網(wǎng)絡中有a個不連接的個體,；(2)在接下來的每一步里引入一個新的節(jié)點，從這個節(jié)點開始一共有a條邊連接到初始的所有節(jié)點上,。新引入的這個節(jié)點按照偏好依附機制連接到初始的某個節(jié)點上,，假設這個節(jié)點為θ；新引入的這個節(jié)點的其他邊則以概率Ut隨機連接到θ的鄰居節(jié)點上,，而以概率1－Ut按照依附偏好機制連接到起初的其他節(jié)點上,。此模型的度分布與無標度模型一樣，當Ut=0時,，這個模型就是無標度模型,。通過改變Ut,，就可以得到不一樣的集聚系數(shù)。

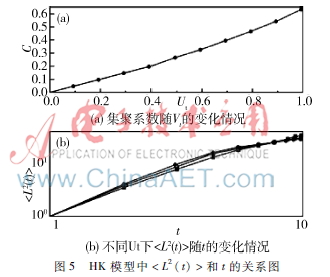
　　圖5（a）顯示了集聚系數(shù)隨Ut的變化情況,，同樣也在HK模型中做了異常行為傳播仿真,，圖5（b）顯示了不同的Ut下，〈L2(t)〉隨t的變化情況,。

　　另外,，從圖5（b）可以看出，集聚系數(shù)的增大使η偏離了數(shù)值2,，此結果和小世界模型相同,。比較圖5（b）與圖4（b）可以看出，HK模型相對來說偏離η=2的幅度更小,，因此,，也就驗證了異常行為更容易在非均勻網(wǎng)絡中進行傳播。同時,，不管是小世界網(wǎng)絡模型還是HK模型,，η的值都是處于1和2之間的。

4結束語

　　對網(wǎng)絡化軟件異常行為的傳播過程進行研究,，能夠提高網(wǎng)絡化軟件系統(tǒng)的穩(wěn)定性與可信性,。本文利用SIR模型對網(wǎng)絡化軟件上的異常行為傳播過程進行了理論分析和實驗模擬。當感染幾率一定時,，聚集系數(shù)C和度分布P(k)都會影響異常行為的傳播,。異常行為的傳播指數(shù)η隨集聚系數(shù)C的增加而變小，隨著非均勻度的增強而變大,。研究異常行為在網(wǎng)絡化軟件中的傳播可以為以后的異常行為控制提供有意義的指導,。它作為網(wǎng)絡化軟件中異常行為研究的一部分，是十分有價值的,。

　　參考文獻

　?。?］ 彭成，楊路明,，滿君豐．網(wǎng)絡化軟件交互行為動態(tài)建模［J］.電子學報,，2013,41（2）：314320.

　　［2］ 何克清,，彭蓉,，劉瑋，等.網(wǎng)絡式軟件［M］.北京：科學出版社,，2008.

　?。?］ HE K Q, PENG R, LIU J, et al. Design methodology of networked software evolution growth based on software patterns ［J］. Journal of Systems Science and Complexity, 2006, 19(2):157181.

　　［4］ PASTORSATORRAS R, VESPIGNANI A. Epidemic spreading in scalefree networks ［J］. Phys. Rev. Lett,2011,86:32003203.

　?。?］ PASTORSATORRAS R, VESPIGNANI A. Epidemics and immunization in scalefree networks ［M］. Berlin: Wiley- VCH,2003.

　?。?］ HETHCOTE H W.The mathematics of infectious diseases ［J］. SIAM Review, 2000, 42（4）: 599653.

　?。?］ COHEN R， HAVLIN S. Scalefree networks are ultrasmall［J］. Phys. Rev. Lett. 2003, 90:058701(14).

　?。?］ FRONEZAK A, FRONEZAK P, HOLYST J A.Meanfield theory for clustering coefficients in BarabasiAlbert networks［J］.Phys.Rev.E,2003,68:046126(14).

　?。?］ 于靜雯,楊冰.基于MapReduce框架下的復雜網(wǎng)絡社團發(fā)現(xiàn)算法［J］.微型機與應用,2014,33(22):7476.

　　［10］ WATTS D J, STROGATZ S H. Collective dynamics of ‘smallword’ networks ［J］. Nature, 1998(393):440442.

　?。?1］ WATTS D J. The‘new’ science of networks ［J］. Publ. Math. Inst. Hung. Acad. Sci., 1960(5):1760.

　?。?2］王健，劉衍珩,，劉雪蓮,等.復雜軟件的級聯(lián)故障建模［J］.計算機學報,，2011,34（6）：11371147.

　　［13］ 周寬久,，蘭文輝,，馮金金,等.基于耦合影響格子的軟件相繼故障研究［J］.計算機科學，2011,38(5):129131,174.

　?。?4］ KANEKO K. Perioddoubling of kinkantikink patterns, quasiperiodicity in antiferrolike structures and spatial intermittency in coupled map lattices ［J］. Prog. Theor. Phys, 1984, 72(3): 480486.

　?。?5］ CHALLET D, LOMBARDONI A. Bug propagation and debugging in asymmetric software structures ［J］. Phys. Rev.E 2004,70(4):10151030.