摘 要： 傳統(tǒng)的K-means算法隨機選取初始聚類中心,，聚類結果不穩(wěn)定,，容易陷入局部最優(yōu)解。針對聚類中心的敏感性,，提出一種優(yōu)化初始聚類中心的K-means算法,。此算法利用數(shù)據集樣本的分布特征計算樣本點的密度并進行分類，在高密度區(qū)域中選擇K個密度最大且相互距離超過某特定閾值的點作為初始聚類中心,，并對低密度區(qū)域的噪聲點單獨處理,。實驗證明，優(yōu)化后的算法能取得更好的聚類效果，且穩(wěn)定性增強,。
關鍵詞： 聚類,；K-means算法；密度,；聚類中心,；噪聲點
0 引言
隨著“信息爆炸”時代的到來，數(shù)據挖掘領域得到人們越來越多的關注,。聚類分析作為數(shù)據挖掘的重要分支,，屬于無監(jiān)督的機器學習方法[1]?；谖镆灶惥鄣乃枷?，聚類分析把樣本點劃分為子簇，使得同一簇中的對象盡可能相似,，而不同簇的對象盡可能相異[2],。目前，聚類已根植于許多應用領域,，包括商務智能,、圖像模式識別、WEB搜索,、生物學和安全等[3],。
K-means算法是目前聚類分析領域中基于劃分的熱門研究課題，具有理論可靠,、算法簡單,、收斂速度快、能有效處理大數(shù)據的特點[4],。但它也存在一些不可避免的問題[5]：（1）聚類數(shù)目k需要預先確定,，經驗的缺乏導致對k的數(shù)值很難界定；（2）聚類結果隨初始聚類中心的不同而變化,，容易陷入局部最優(yōu)解,；（3）對局部極值點敏感，嚴重影響聚類結果的準確性,。
本文提出一種基于密度優(yōu)化初始聚類中心的方法,，使其盡可能有代表性地反映數(shù)據的分布特征。利用數(shù)據集樣本的點密度,，對樣本集劃分高低密度集,，選取高密度集合中的k個相距較遠、密度最大的樣本作為初始聚類中心,，避免初始聚類中心位于同一類簇的缺陷,，同時對噪聲點進行單獨處理,，減小其對聚類結果的影響。
1 K-means算法介紹及相關研究
K-means算法是基于劃分的聚類算法之一,，基本思想[6]是：從包含n個對象的數(shù)據集中隨機選取k個樣本點作為初始聚類中心，對于剩下的每個對象,，計算其與各個聚類中心的距離,，將它分配到最近的聚類，并重新計算聚類中心,，再將所有的樣本點依據最近距離原則分配到相應的聚類簇中,，不斷地迭代直到分配穩(wěn)定，即聚類誤差平方和E收斂,。
K-means算法簡單,，且適用于大規(guī)模數(shù)據量，但初始聚類中心的選取直接影響算法的聚類結果,，算法的迭代次數(shù)依賴于初始聚類中心和實際聚類中心的偏差,，因此，選取一組合適的初始聚類中心非常重要[7],。很多國內外學者從不同角度對該算法聚類中心的選取進行了改進,。陸林華[8]對遺傳算法進行優(yōu)化，將遺傳算法的全局搜索能力與K-means算法的局部搜索能力相結合,；KAUFMAN L等[9]提出一種啟發(fā)式方法,，估計數(shù)據點的局部密度，并以此啟發(fā)選擇初始聚類中心,；袁方等[10]提出給予樣本相似度和通過合適權值來初始化聚類的方法,；Huang J[11]提出一種變量自動加權方法，ALSABTI[12]利用k-d樹結構改進K-means算法,；汪中[5]等人采用密度敏感的相似性度量計算數(shù)據對象的密度,，啟發(fā)式地生成初始聚類中心；韓凌波[13]等人通過計算每個數(shù)據對象的密度參數(shù)選取k個處于高密度分布的點作為初始聚類中心,；賴玉霞[14]等人采用聚類對象分布密度方法,，選擇相互距離最遠的k個處于高密度區(qū)域的點作為初始聚類中心；王賽芳[15]等人通過計算點密度來選取初始聚類中心,。
2 基于密度改進的K-means算法
傳統(tǒng)的K-means算法對初始聚類中心敏感,，聚類結果隨不同的初始中心而波動。隨機選取的初始聚類中心有可能是一些孤立點或噪聲點,，或者不同類簇的初始聚類中心位于同一個類簇,，導致聚類結果可能偏離樣本的真實分布，得到錯誤的聚類結果,，使聚類的收斂速度緩慢甚至難以收斂,。選取相距較遠的樣本作為初始聚類中心，可避免初始聚類中心位于同一類簇的缺陷，但對噪聲點敏感,；參考文獻[11-12]解決了噪聲點的問題,，但由于涉及到密度調節(jié)系數(shù)或噪聲調節(jié)系數(shù)，聚類結果直接依賴于參數(shù)的選擇,。主觀性強,，如果參數(shù)選擇不好，聚類結果將變得很差,。
針對上述局限性,，本文提出一種基于點密度優(yōu)化初始聚類中心選取的方式。在樣本點空間中,，一般認為高密度區(qū)域的點會被低密度區(qū)域的點分割,，而噪聲點往往處于低密度區(qū)域。同時,，在以歐氏距離作為相似性度量標準的情況下,，相互距離遠的k個樣本點往往比隨機選取更具有代表性。因此,，在劃分出含有噪聲點的低密度區(qū)域后,，本文在高密度區(qū)域選取k個相互距離超過某閾值，且密度最大的樣本點作為初始聚類中心,，即改進K-means算法中的隨機選取初始聚類中心,。
2.1 基本定義
設給定含有n個樣本點的數(shù)據集合X={xi|xi∈R，i=1,，2,，…，n},，k個聚類類別Cj（j=1,，2，…,，k,，k<n），k個初始聚類中心ncj（j=1,，2,，…，k）,。有如下定義：
定義1 任意兩個樣本點間的歐氏距離
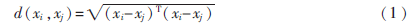
定義2 聚類中心（每個聚類簇的樣本點的均值）
定義3 聚類誤差平方和
聚類誤差平方和是數(shù)據集所有對象與它所在簇的聚類中心的平方誤差的總和,。聚類誤差平方和越大，說明對象與聚類中心的距離越大,，簇內的相似度越低,，反之亦然,。聚類誤差平方和應盡可能小，從而使生成的結果簇盡可能緊湊和獨立,。
定義4 點密度
對數(shù)據集X中的樣本點x,，以x為圓心，r（r>0）為半徑的球域內所包含的樣本點的個數(shù)稱為x的密度,，記為D（x）,，即
D（x）=|{p|y（x，p）≤r,，p∈X}|（4）
式中，y（x,，p）表示樣本點x與p的距離,。通過比較，本文選擇以歐氏距離作為距離度量,，即y（x,，p）=d（x，p）,，r為設定的距離閾值,。D（x）越大，樣本點所處區(qū)域密度越高,。
定義5 噪聲點
對于數(shù)據集X中的樣本點x,，若D（x）<?琢MD（x），則稱x為噪聲點,。其中,，MD（x）為所有樣本點的密度平均值，即
2.2 初始聚類中心的優(yōu)化算法
基于密度優(yōu)化初始聚類中心的基本思想是：首先計算樣本集中每個樣本點的密度D（x）,，并通過與整個樣本集平均密度MD（x）的比較,，將其劃分給高密度集M或低密度集N。選取集合M中密度最大的樣本點作為第一個初始聚類中心nc1,，將其從集合M中剔除,；接著從集合M中選取與nc1距離超過距離閾值r，且密度最大的點作為第二個初始聚類中心nc2,，以此類推,，直到選取了k個初始聚類中心。
基于密度優(yōu)化初始聚類中心算法的具體步驟如下：
輸入：聚類簇的數(shù)目k以及包含n個對象的數(shù)據集X
輸出：初始聚類中心集合nc,，高密度集M和低密度集N
?。?）根據式（1），計算樣本集兩兩樣本點間的距離,，構造距離矩陣D,；
?。?）根據式（4）和式（5），計算樣本集中每個樣本點的密度D（x）,，以及整個樣本集的平均密度MD（x）,；
（3）根據MD（x）,，對樣本點進行劃分,，依次歸類進高密度集M或低密度集N；
?。?）選取M中密度最大的樣本點作為第一個初始聚類中心nc1,，并將其放入集合nc中，即nc=nc∪{nc1},；
?。?）選取下一個初始聚類中心nc2，并將其放入集合nc中,，即nc=nc∪{nc2},。其中，nc2應滿足：①d（nc1,，nc2）≥r,；②D（nc2）=max{D（x）|x∈X-nc}；
?。?）重復步驟（5）,，直到選取k個初始聚類中心。
2.3 噪聲點的處理
聚類過程中,，本文將數(shù)據樣本劃分為高密度集和低密度集,，其中，低密度集就是噪聲點集合,。選取完k個初始聚類中心后,，首先對集合M中的樣本點進行K-means聚類，得到k個聚類和k個聚類中心,。接著依據最小距離原則,，將集合N中的噪聲點分配到各個聚類中，完成所有樣本點的分配聚類,。由于避免了噪聲點對聚類過程的參與,，減少了其對聚類中心的影響，改善了聚類效果,。
3 實驗結果與分析
為了驗證本文算法的有效性,，選用MATLAB語言編程環(huán)境，對UCI數(shù)據集進行測試,，并與參考文獻[5,，12,，14]及傳統(tǒng)K-means算法的聚類結果進行比較。對算法聚類結果的評價標準包含很多種,，本文采用兩種度量指標：聚類準確率和聚類時間,。利用聚類準確率來度量算法的有效性，利用聚類時間來度量算法的執(zhí)行效率,。
3.1 數(shù)據集描述及參數(shù)設定
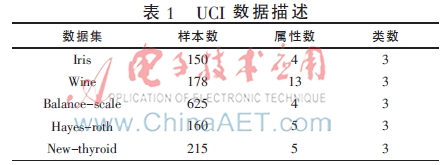
UCI數(shù)據集是國際上專門用來測試機器學習,、數(shù)據挖掘算法的公共數(shù)據庫，庫中的數(shù)據都有確定的分類,，因此可以用準確率來直觀地反映聚類算法的質量,。在此，本文選擇數(shù)據庫中的Iris,、Wine,、Balance-scale、Hayes-roth以及New-thyroid 5組數(shù)據作為測試數(shù)據,，如表1。
3.2 實驗結果
根據經驗,，將改進算法的密度球域半徑r設為樣本點兩兩間的平均歐式距離,；噪聲點劃分閾值0<
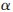≤1，一般取值為1,。所有算法均在表1給出的數(shù)據集上進行實驗,，所有評價結果均為在數(shù)據集上實驗執(zhí)行100次后取平均值。表2為選取五種不同初始聚類中心情況下算法在UCI數(shù)據集上的聚類準確率的比較,，表3為各算法的聚類時間比較,。
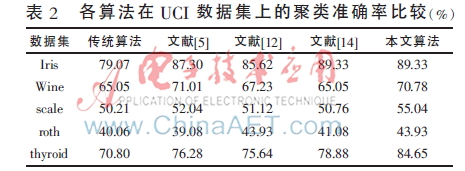
由表2聚類準確率的比較可知，在Iris數(shù)據集上,，本文算法的聚類準確率與參考文獻[14]中的算法一致,，高于傳統(tǒng)K-means算法和參考文獻[5，12],；在Wine數(shù)據集上,，本文算法的準確率略低于參考文獻[5]，但高于參考文獻[12,，14]及傳統(tǒng)K-means,；在Hayes-roth數(shù)據集上，本文算法的聚類準確率與參考文獻[12]一致,，高于參考文獻[5,、14]及傳統(tǒng)算法；而在其他數(shù)據集上,，文本算法的聚類準確率高于其他四種算法,。由此可見,，本文算法相較于其他算法，聚類準確性更高,。
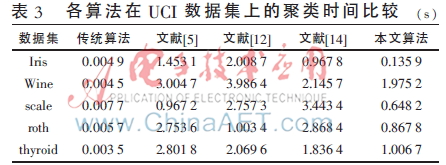
由表3各算法聚類時間的比較可知,，傳統(tǒng)K-means算法的運行時間最短；本文算法的聚類運行時間優(yōu)于參考文獻[12,，14],，具有更快的收斂速度；但與參考文獻[5]相比,，在Scale和Wine數(shù)據集上,，本文算法的聚類速度略有遜色。就總體時間分析而言,，本文的算法優(yōu)于其他算法,，但不如傳統(tǒng)K-means算法的速度快。這是因為改進后的算法增加了選擇初始中心這一環(huán)節(jié),，造成了一定的時間損耗,，但優(yōu)化后的初始聚類中心能更好地表達數(shù)據的分布特征，有效縮短聚類過程,，因此在一定程度上又能減少時間的損耗,。
以上結果表明，相較于其他優(yōu)化初始聚類中心的K-means算法,，本文算法不僅可以獲得更好的聚類效果,，同時也能縮短聚類時間。
4 結束語
K-means算法應用廣泛,，但由于其過分依賴于初始化,，聚類結果隨初始中心的變化而波動，難以保證優(yōu)良的性能,。本文基于密度,，有效改進了初始中心點的選取，克服了傳統(tǒng)算法敏感且聚類效果容易陷入局部最優(yōu)的缺陷,，同時在一定程度上避免了噪聲數(shù)據對聚類結果的影響,。實驗結果證明，該算法能大大提高聚類的準確性,。
參考文獻
[1] 毛國君,，段立娟，王實,，等．數(shù)據挖掘原理與算法[M]．北京：清華大學出版社,，2005．
[2] 朱明．數(shù)據挖掘[M]．合肥：中國科學技術大學出版社，2002．
[3] Han Jiawei,， KAMBER M．數(shù)據挖掘概念與技術[M]．范明,，孟小峰,，譯．北京：機械工業(yè)出版社，2000．
[4] 謝娟英,，郭文娟.基于樣本空間分布密度的初始聚類中心優(yōu)化K-均值算法[J].計算機應用研究,，2012，29（3）：888-890.
[5] 汪中,，劉貴全,，陳恩紅.一種優(yōu)化初始中心點的K-means算法[J].模式識別與人工智能，2009,，22（2）：300-302.
[6] 莫錦萍,，陳琴，馬琳,，等.一種新的K-Means蟻群聚類算法[J].廣西科學學院學報,，2008，24（4）：284-286.
[7] 柯良文,，王靖.基于用戶相似度遷移的協(xié)同過濾推薦算法[J].微型機與應用,，2014，33（14）：71-74.
[8] 陸林華,，王波.一種改進的遺傳聚類算法[J].計算機工程與應用,，2007，43（21）：170-172.
[9] KAUFMAN L,， ROUSSEEUW P J． Finding groups in data：all intro-duction to cluster analysis[M]． New York： Wileys，1990．
[10] 袁方,，孟增輝,，于戈.對K-means聚類算法的改進[J].計算機工程與應用，2004,，40（36）：177-178,，232.
[11] HUANG J Z， NG M K,， HONGQIALLG R,， et al． Automated variable weighting in K-means type clustering[J]． IEEE Trans on Pattern Analysis and Machine Intelligence， 2005,，27（5）：657-668.
[12] ALSABTI K,， RANKA S， SINGH V． An efficient K-means clustering algorithm[C]. IPPS/SPDP Workshop on High Performance Data Mining． Orlando,， Florida,， 1998： 9-15.
[13] 韓凌波，王強,，蔣正峰,，等．一種改進的K-means初始聚類中心選取算法[J]．計算機工程與應用,，2010，46（17）：150-152．
[14] 賴玉霞,，劉建平．K-means算法的初始聚類中心的優(yōu)化[J]．計算機工程與應用,，2008，44（10）：147-149．
[15] 王賽芳,，戴芳,，王萬斌，等．基于初始聚類中心優(yōu)化的K-均值算法[J]．計算機工程與科學,，2010,，32（10）：105-107．