摘 要: AC(Aho-Corasick)自動機是經(jīng)典的多模式匹配算法,但在模式串字符集較大的情況下,AC自動機的存儲開銷較大。為降低存儲開銷提出了存儲優(yōu)化的多模式匹配算法SMMA,該算法在Trie樹建立階段利用正向表來存儲每個狀態(tài)的后續(xù)狀態(tài)指針以及失配指針,而無需存儲字符集所有字符的后繼指針,從而壓縮了每個狀態(tài)的儲存空間。實驗表明,所提出的算法與AC自動機算法在時間效率上相近,但極大地降低了存儲開銷。
關(guān)鍵詞: 模式匹配;AC自動機;Trie樹
0 引言
模式匹配算法一直是信息領(lǐng)域的研究熱點,廣泛應用于入侵檢測、生物信息學、模式識別等領(lǐng)域[1]。模式匹配算法可以分為單模式匹配算法[2-3]和多模式匹配算法[4-8]。Aho-Corasick算法[4](以下簡稱AC算法)是經(jīng)典的多模式匹配算法,它把所有模式串構(gòu)建成Trie樹,并進一步預處理得到有限狀態(tài)自動機,對主串的一次掃描即可完成所有模式串的匹配。Commentz-Walter算法(CW算法)[5]建立反向自動機,在模式匹配階段利用壞字規(guī)則和好后綴規(guī)則,在失配時滑動最大的距離,實現(xiàn)了模式串的跳躍匹配,減少了時間開銷。Wu-Manber(WM)算法[6]對多模式串進行預處理,建立三張映射表進行部分匹配,最后進行全模式匹配,提高了效率。參考文獻[7]提出了改進的多模式匹配算法,在DFSA算法的基礎(chǔ)上,結(jié)合QS算法[8]思想,利用匹配過程中匹配失敗信息,跳過盡可能多的字符。
AC算法的一個不足是需要為自動機每個狀態(tài)分配空間,在模式串字符集比較大的情況下,算法空間復雜度比較大。極端情況下,需要使用外存來保存匹配過程的中間信息,嚴重影響算法效率。為此,參考文獻[9]提出基于異構(gòu)隱式存儲的多模式匹配算法,從橫向扇出壓縮與縱向路徑壓縮入手,減少了空間開銷,但算法的空間壓縮率不高,且算法效率有所降低。參考文獻[10]通過選擇性分群減小匹配算法的空間復雜度,有效解決導致DFA狀態(tài)膨脹的問題。參考文獻[11]提出了對DFA進行高效存儲的方法,從DFA狀態(tài)數(shù)目和狀態(tài)轉(zhuǎn)移數(shù)目兩方面進行壓縮。在復合的FSM中,利用新的正則特征,進一步存儲壓縮,但是算法實現(xiàn)復雜、壓縮性能不穩(wěn)定、時間效率不高,實際工程應用不理想。為了減少自動機各結(jié)點的存儲空間,TUCK N等人[12]在每個結(jié)點中增加一個位圖數(shù)據(jù),以記錄當前結(jié)點所有的下一層結(jié)點的狀態(tài),壓縮了存儲空間。AC-bitmap[13]則將自動機的所有結(jié)點按模式樹結(jié)構(gòu)的層數(shù)進行劃分,使得兩種存儲方式共存,以壓縮算法的存儲空間。但是,基于位圖壓縮自動機算法要求采用連續(xù)的地址空間存儲,以加快轉(zhuǎn)移時的查找速度,算法實現(xiàn)比較復雜,并且算法要求為每個結(jié)點存儲一個位圖信息,隨著字母表的不斷增大,其存儲空間將迅速增大。
為更好地優(yōu)化多模式匹配算法的空間復雜度,本文提出了基于存儲優(yōu)化的多模式匹配算法(Storage-optimized Multi-pattern Matching Algorithm,SMMA)。該算法在建立Trie樹時,動態(tài)建立自動機上每個狀態(tài)結(jié)點的字符集,只保留Trie樹上的有效路徑信息,以保證用最小的空間代價存儲模式串的所有信息,避免了無效字符路徑的創(chuàng)建,壓縮了儲存空間。在模式匹配階段,通過在自動機上的狀態(tài)轉(zhuǎn)移完成匹配。在保持算法時間復雜度不變的情況下,顯著降低了算法的空間開銷。
1 相關(guān)概念
定義1 設(shè)p為Trie樹的一個結(jié)點,則Trie樹中從根結(jié)點到結(jié)點p的簡單路徑上所有字符組成的字符序列稱為結(jié)點p的路徑,記為path(p)。構(gòu)成path(p)中字符的個數(shù)稱為結(jié)點p的路徑長度,記為Len(p)。
定義2 設(shè)p為Trie樹的一個結(jié)點,若結(jié)點p的路徑path(p)是一個模式串,則稱結(jié)點p為匹配點,否則稱為非匹配點。
定義3 自動機M是一個五元組:M=(Q,?撞,g,q0,F(xiàn))。其中:Q是有窮狀態(tài)集;?撞是字母表;g是轉(zhuǎn)移函數(shù),轉(zhuǎn)向下一個狀態(tài);q0是初始狀態(tài);F是自動機M上的終止狀態(tài)集。
定義4 設(shè)pa、p為自動機上的狀態(tài)結(jié)點,c為字符集中的一個字符,若?堝p,pa,c,path(p)=c+path(pa),p∈Q,pa∈Q,c∈(sigma),則稱pa為p的后綴結(jié)點,記為S(p)。
定義5 設(shè)p為Trie樹的一個結(jié)點,當且僅當結(jié)點p或其后綴結(jié)點為匹配點,結(jié)點p具有匹配性。
定義6 設(shè)p為自動機上的一個狀態(tài)結(jié)點,則稱Len(S(p))為結(jié)點p的匹配長度。
2 SMMA模式匹配算法
2.1 SMMA算法的基本思想
SMMA算法包括三個階段:建立Trie樹階段、建立自動機階段和模式匹配階段。SMMA算法在建立Trie樹時,并不像傳統(tǒng)的AC自動機那樣為每一個結(jié)點開辟字符集大小的后繼指針空間,而是根據(jù)具體的模式串信息動態(tài)地擴增Trie樹結(jié)點的后繼指針空間,因此只保留Trie樹上的有效路徑信息,避免了無效字符路徑的創(chuàng)建,壓縮了儲存空間。在實現(xiàn)時,SMMA用正向表來存儲Trie樹。
建立自動機和模式匹配階段都有查詢當前結(jié)點cur的某個后繼ch的操作goto(cur,ch)。若當前結(jié)點的后繼結(jié)點不存在,則繼續(xù)查詢goto(fail[cur],ch)。為了快速求得所需的后繼結(jié)點,本文用Next(cur,ch)函數(shù)獲得后繼結(jié)點編號,Next()函數(shù)的實現(xiàn)在2.3節(jié)介紹。
2.2 正向表
正向表是一種邊表,空間代價與鄰接表相當,由于正向表沒有使用指針而減少了一部分結(jié)構(gòu)性開銷,在存儲樹和稀疏圖時具有巨大優(yōu)勢。將正向表應用于AC自動機多模式匹配算法,可以壓縮所需的存儲空間,減少算法空間開銷。
2.3 結(jié)點后繼獲得函數(shù)Next()
算法1 結(jié)點后繼獲得函數(shù)Next(x,c)
輸入:當前結(jié)點編號x,轉(zhuǎn)移字符c
輸出:當前結(jié)點x以字符c為轉(zhuǎn)移條件的后繼結(jié)點編號
①初始化邊指針i←head[x];
②若邊指針i為空,則轉(zhuǎn)到⑤;
③若edge[i].ch==c,則返回edge[i].to結(jié)點的編號;
④邊指針i指向下一條邊:i←edge[i].next,并轉(zhuǎn)到②;
⑤若結(jié)點x為根結(jié)點,則返回0(根結(jié)點編號);
⑥遞歸調(diào)用結(jié)點后繼獲得函數(shù),返回Next(tree[x].fail,c)。
2.4 建立Trie樹階段
算法2 模式串插入算法
輸入:待插入字符串a(chǎn)rr[],待插入字符串的標號index
輸出:將字符串a(chǎn)rr[]插入Trie樹
①初始化字符指針i←0,設(shè)置當前結(jié)點指針cur←0(Trie樹根結(jié)點),計算字符串長度len←strlen(arr);
②若i≥len,則轉(zhuǎn)到{13};
③初始化邊指針j←head[cur];
④若邊指針j為空,則轉(zhuǎn)到⑦;
⑤若edge[j].ch==arr[i],則轉(zhuǎn)到⑦;
⑥邊指針j指向下一條邊:j←edge[j].next,并轉(zhuǎn)到④;
⑦若邊指針j非空,則轉(zhuǎn)到⑨;
⑧清空結(jié)點編號為nodeNo的結(jié)點,增加一條以cur為源點,以nodeNo為終點,邊上的字符為arr[i]的有向邊,并依次設(shè)置cur←nodeNo,nodeNo←nodeNo+1,轉(zhuǎn)到⑩;
⑨將edge[j].to結(jié)點設(shè)置為當前結(jié)點:cur←edge[j].to;
⑩若i!=len-1,則轉(zhuǎn)到{12};
{11}更新當前結(jié)點信息:tree[cur].end←index,tree[cur].len←len,tree[cur].isDanger←True;
{12}設(shè)置i←i+1,轉(zhuǎn)到②;
{13}插入完成,返回。
2.5 建立自動機階段
建立自動機是實現(xiàn)SMMA算法的關(guān)鍵。建立自動機時,需要對Trie樹進行廣度優(yōu)先遍歷(Breadth First Search,BFS),預處理Trie樹上每個結(jié)點的后綴結(jié)點、匹配性等信息,以便在模式匹配階段快速轉(zhuǎn)移狀態(tài),在失配時,能根據(jù)建立自動機階段預處理出的信息快速確定所需要的后繼狀態(tài)。利用Next()函數(shù)快速返回其后綴結(jié)點的編號。
算法3 自動機建立算法
輸入:Trie樹Tree[]
輸出:建立自動機
①初始化隊列Q的隊頭指針l和隊尾指針h:l←0,h←0,并設(shè)置邊指針i←head[0];
②若邊指針i為空,則轉(zhuǎn)到⑤;
③將edge[i].to結(jié)點放入隊尾:Q[h]←edge[i].to,h←h+1,并設(shè)置edge[i].to結(jié)點的后綴結(jié)點為自動機的起始結(jié)點:tree[edge[i].to].fail←0;
④邊指針i指向下一條邊:i←edge[i].next,并轉(zhuǎn)到②;
⑤若l≥h,則轉(zhuǎn)到⑩;
⑥設(shè)置當前結(jié)點指針cur:cur←Q[l],l←l+1,并設(shè)置邊指針i←head[cur];
⑦若邊指針為空,則轉(zhuǎn)到⑤;
⑧利用結(jié)點后繼獲得函數(shù)計算edge[i].to結(jié)點的后綴結(jié)點:tree[edge[i].to].fail←child(tree[cur].fail,edge[i].ch),更新edge[i].to結(jié)點的信息并將該結(jié)點放入隊尾:tree[edge[i].to].isDanger←tree[edge[i].to].isDanger|tree[tree[edge[i].to].fail].isDanger,Q[h]←edge[i].to,h←h+1;
⑨邊指針i指向下一條邊:i←edge[i].next,并轉(zhuǎn)到⑦;
⑩自動機建立完成,返回。
2.6 模式匹配階段
從自動機的初始狀態(tài)結(jié)點開始,以主串中各字符為轉(zhuǎn)移條件,用Next()函數(shù)返回當前結(jié)點的后繼結(jié)點,再將當前結(jié)點指針cur轉(zhuǎn)移到該后繼結(jié)點上。若該結(jié)點未被訪問并且具有匹配性,則設(shè)置臨時結(jié)點指針p,并賦初值為cur,同時標記該結(jié)點為已訪問的結(jié)點,根據(jù)具體需要獲取數(shù)據(jù)信息,再將結(jié)點指針p轉(zhuǎn)移到結(jié)點p的后綴結(jié)點上。
3 算法的時空復雜度
設(shè)自動機的狀態(tài)結(jié)點個數(shù)為N,字符集規(guī)模為∑,文本主串長度為L,模式串集合大小為P,模式串集合的總規(guī)模為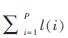 ,其中,l(i)為第i個模式串的長度。
,其中,l(i)為第i個模式串的長度。
3.1 空間復雜度分析
在建立自動機階段,AC算法需要對每個狀態(tài)結(jié)點建立字符集大小的空間,空間復雜度為O(N*?撞)。SMMA算法對于自動機的每個狀態(tài)結(jié)點只保留必要的結(jié)點信息,其所占用的存儲空間大小與自動機的結(jié)點個數(shù)呈線性相關(guān),因此SMMA算法存儲自動機的空間復雜度為O(N)。AC算法和SMMA算法都需要存儲待匹配的文本主串和各模式串的信息,存儲待匹配的文本主串的空間復雜度為O(L),存儲模式串集合具體信息的空間復雜度為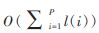 )。
)。
因此,AC算法的總空間復雜度為 ∑+L),SMMA算法的總空間復雜度為
∑+L),SMMA算法的總空間復雜度為 +L)。但隨著字符集規(guī)模∑和模式串集合P的增大,AC算法的空間消耗的增長速度遠快于SMMA算法。
+L)。但隨著字符集規(guī)模∑和模式串集合P的增大,AC算法的空間消耗的增長速度遠快于SMMA算法。
3.2 時間復雜度分析
在建立Trie樹階段,在插入模式串的每個字符時都需要遍歷當前結(jié)點的所有后繼結(jié)點,該階段最差時間復雜度為 。
。
在建立自動機階段,SMMA算法需要通過BFS序遍歷所有結(jié)點,預處理出每個狀態(tài)結(jié)點的后綴結(jié)點、匹配性等重要信息,對于Trie樹上的每一條從根到葉的路徑上的結(jié)點來說,它們的后綴結(jié)點離根的距離一般是逐層增長的,若不是,則進行多次回溯,而回溯的總次數(shù)不會大于路徑上的結(jié)點個數(shù),其平均時間復雜度為O(l(i)*∑),所以建立自動機階段的最差時間復雜度為O(N*∑)。
在主串匹配階段,SMMA算法轉(zhuǎn)移所需的時間復雜度為O(∑)。由于可能出現(xiàn)主串失配的情況而需要多次回溯查找后繼結(jié)點,但每次失配時,回溯查詢的次數(shù)最多僅為當前結(jié)點所在層的深度。因此最壞情況下進行了主串長度次回溯,其平均時間復雜度為O(L*∑),而設(shè)立臨時結(jié)點指針回溯查詢具有相同后綴的模式串的次數(shù)不會超過自動機的狀態(tài)結(jié)點數(shù),其最差時間復雜度為O(N),因此主串匹配階段的總時間復雜度為O(L*∑+N)。
AC算法在建立Trie樹階段的時間復雜度為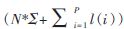 ,在建立自動機階段的時間復雜度為O(N*∑),在主串匹配階段的時間復雜度為O(L)。
,在建立自動機階段的時間復雜度為O(N*∑),在主串匹配階段的時間復雜度為O(L)。
綜上所述,SMMA的總時間復雜度為O(∑(l(i)*∑)+N*∑+L*∑+N),在字符集規(guī)模?撞和模式串集合P不斷增大的情況下,SMMA算法和AC算法的時間開銷具有相同數(shù)量級的增長速度。
4 實驗仿真
實驗部分測試了SMMA算法,同時比較SMMA算法和AC算法、AC_bitmap算法的時間開銷和空間開銷。本文隨機產(chǎn)生100 KB文本主串,并給出不同字符集大小的模式串集合,各模式串長度均為100 B,程序運行結(jié)果:處理模式串集合,給出每個模式串與主串的關(guān)系信息,例如模式串是否匹配、模式串在主串中的位置等。實驗所得數(shù)據(jù)如圖1~圖6所示,其中P為模式串規(guī)模,∑為字符集大小。


分析可見SMMA算法在漸近時間復雜度上與AC算法相同,僅在常數(shù)上有所增加,在模式串規(guī)模擴大、字符集大小增大的情況下,SMMA算法極大地減少了多模式匹配算法的空間消耗。SMMA算法與AC_bitmap算法的時空效率十分接近,平均情況下,SMMA算法的時間效率比AC_bitmap算法提升了5.8%,空間消耗減少了16.3%。但隨著模式串規(guī)模和字符集大小的增加,SMMA算法的優(yōu)勢更加明顯。
5 結(jié)論
本文提出的SMMA算法避免了無效字符路徑的創(chuàng)建,壓縮了多模式匹配算法的儲存空間,優(yōu)化了空間效率,有效地改進了AC算法在存儲空間上的缺陷。實驗結(jié)果表明,SMMA算法具有高效的時空效率,在模式串規(guī)模與字符集規(guī)模增大的情況下,優(yōu)勢更加明顯。
參考文獻
[1] 王培鳳,李莉.基于Aho-Corasick算法的多模式匹配算法研究[J].計算機應用研究,2011,28(4):1251-1259.
[2] KNUTH D E, MORRIS J H. Pattern matching in strings[J]. SIAM Journal on Computing,1977,6(2):323-350.
[3] BOYER R S, MOORE J S. A fast string searching algorithm [J]. Communications of the ACM, 1988,20(10):762-772.
[4] AHO A V, CORASICK M J. Efficient string matching: an aid to bibliographic search[J]. Communications of the ACM,1975,18(6):330-340.
[5] COMMENTS W R. A string matching algorithm fast on the average[C]. Proceedings of the 6th Colloquium on Automata, Language and Programming[S.1.]: Springer-Verlag, 1979.
[6] Wu Sun, MANBER U. A fast algorithm for multi-pattern searching[Z]. Taiwan, China: Department of Computer Science, Chung-Cheng University, 1994.
[7] 王永成,沈州,許一震.改進的多模式匹配算法[J].計算機研究與發(fā)展,2002,39(1):55-60.
[8] SUNDAY D M. A very fast substring search algorithm[J]. Communications of the ACM, 1990,33(8):132-142.
[9] 李志東,楊武,張汝波,等.基于異構(gòu)隱式存儲的多模式匹配算法[J].通信學報,2009,30(3):119-124.
[10] 徐乾,鄂躍鵬,葛敬國,等.深度包檢測中一種高效的正則表達式壓縮算法[J].軟件學報,2009,20(8):2214-2226.
[11] 于強,霍紅衛(wèi).一組提高存儲效率的深度包檢測算法[J].軟件學報,2011,22(1):149-163.
[12] TUCK N, SHERWOOD T, CALDER T, et al. Deterministic memory efficient string matching algorithms for intrusion detection[C]. Proceedings of the 23rd Annual Joint Conference of IEEE Computer and Communications Societies, New Jersey: IEEE Press, 2004: 2628-2639.
[13] 張元競,張偉哲.一種基于位圖的多模式匹配算法[J].哈爾濱工業(yè)大學學報,2010,42(2):277-280.

