0 引言

    MIMO-OFDM系統(tǒng)憑借其系統(tǒng)容量大,、抗干擾能力強等優(yōu)點,，成為新一代無線通信領域的核心技術^[1-3]。由于MIMO-OFDM對延時和頻偏很敏感,，為保證接收端能夠正確解調,，必須要進行時頻同步^[2-3]。此外,，由于MIMO-OFDM系統(tǒng)中有多根天線,，其相互間的干擾使得同步更加困難^[3]。

    文獻[4]首次提出使用相互正交的訓練序列,，將OFDM系統(tǒng)中的SC算法應用到MIMO-OFDM系統(tǒng)中,，解決了各天線間的相互干擾問題^[5]。文獻[6]利用各天線分時發(fā)送訓練序列來保證時域上的正交性,，但是在天線較多時占用較多時域資源,。以上兩種方法在時間同步前都需要進行幀檢測，補償頻偏后再進行符號同步才能得出正確的定時位置,，因而運算量大,，并且時間同步性能易受到頻偏補償性能的影響。文獻[7]提出了WPS算法,，利用CAZAC序列良好的自相關性,，使得定時性能有了顯著提高，但是沒有考慮到頻偏對定時位置的影響,。文獻[8]使用循環(huán)的延遲序列,，采用互相關和自相關結合的方法進行定時同步，性能良好,，但是依然受到頻偏影響,，在頻偏補償之后需要對定時位置進行修正。本文基于WPS算法,，提供了一種改進的前導序列結構和定時同步方法,，該方法僅需一步便能完成整個時間同步,，定時結果不受頻偏影響，而且同時還能估計出整數倍頻偏,。仿真結果表明,，在AWGN信道和多徑信道下，該同步方法都具有良好的性能,。

1 MIMO-OFDM系統(tǒng)模型

    MIMO-OFDM系統(tǒng)原理框圖如圖1所示,。

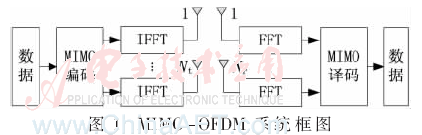
    各發(fā)射天線發(fā)送的OFDM符號可表示為：

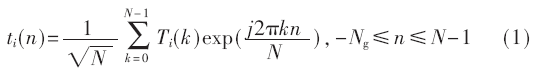
其中，i表示發(fā)射天線序號,，最大為N_t,；N表示IFFT變換的點數，也即系統(tǒng)所用子載波個數,；T_i(k)為第i個發(fā)射天線,、第k個子載波上的調制數據；N_g為消除OFDM符號間干擾的循環(huán)前綴的長度,。

    在高斯信道下,，接收天線接收到的基帶信號可表示為：

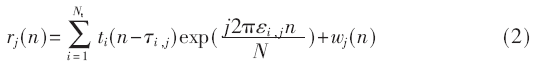
其中，j表示接收天線序號,，最大為N_r,；τ_i，j和ε_i,，j分別表示第i條發(fā)射天線到第j條接收天線的時間延遲和頻率偏移,，?著ij包括整數部分和小數部分，在系統(tǒng)同步過程中需要分別估計,；ω_j(n)表示第j根天線上接收到的AWGN總和,。

2 時間同步方法分析

2.1 WPS定時同步算法

    圖2所示為WPS算法使用的同步序列結構。

    該前導序列由長度為N的CAZAC序列構成,。其生成表達式如下^[9]：

    容易看出,，CAZAC序列的自相關函數是理想的二值函數，因此將其循環(huán)移位后得到的序列和原序列相互正交,，保證了各發(fā)射天線上的序列正交性,。

    由式(3)易知，生成的CAZAC序列還具有自反特性,，如下式：

    只有在訓練序列起始處,，判決函數M_i(d)才能取得最大值，其余位置上的取值均接近于零,，如圖3(a)所示,?？梢钥闯?，定時函數的峰值尖銳,，很容易得出定時點位置。

    引入頻偏?著之后,，判決函數峰值雖然依然尖銳,，但是峰值點位置會有一定的移位，影響定時點位置的判斷,，如圖3(b)所示,。

2.2 改進的前導序列結構和時間同步方案

2.2.1 改進的前導序列結構

    由于WPS算法的定時準確性受頻偏的影響，因此對同步序列結構進行一定的改進,，采用如圖4所示的序列結構,。

    該序列占用2個OFDM符號長度，由周期分別為N_c和N的CAZAC序列組成,，N=2N_c,。各天線上的序列由CAZAC序列循環(huán)移位得到。若第1根發(fā)射天線上的序列為c(n),，則第i根發(fā)射天線上的序列可以表示為c(n-(i-1)·D),，D表示循環(huán)移位數。

    當存在頻偏ε時,，將接收端接收到的信號同本地序列c(n)進行互相關如下：

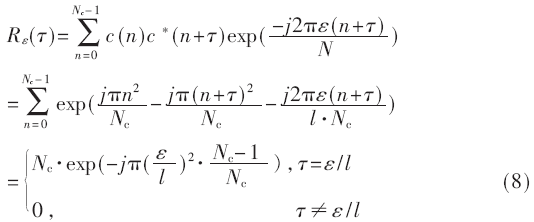
其中l(wèi)=N/N_c,。對比式(5)和式(8)可以看出：當存在頻偏時，互相關函數峰值位置相對理想位置有[ε/l]長度的移位,。

2.2.2 改進的時間同步算法

    本文提出的方法利用接收信號同本地序列進行互相關來進行定時同步,。假設本地序列分別為長度為N_c的c₁(n)和長度為N的c₂(n)，則判決函數可表示為：

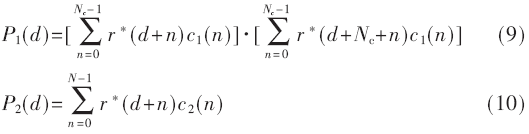
    在P₁(d)和P₂(d)分別取得最大值處即為訓練序列c₁(n)和c₂(n)的起始位置處,。

    由于信號傳輸過程中存在頻偏ε,，由式(8)可知，求得的P₁(d),、P₂(d)的峰值位置相對于理想定時點分別有[ε/2]和[ε]的移位,，如圖5所示。

    與WPS算法相比,，本文采用的方法雖然增加了訓練序列的長度,，占用了一定的信道資源，但是能夠直接地得出準確的定時點,，使定時不受頻偏影響,，并且在定時的同時能夠估計出整數倍頻偏，縮短了同步過程,，從而降低了系統(tǒng)同步的復雜度,。

3 仿真與比較

    參考IEEE802.11n標準^[10]，在高斯信道和多徑信道下對本文提出的算法和WPS算法分別進行了仿真,。天線數為2發(fā)1收,，更多天線數目的情況可由此推廣得到,。仿真各參數如表1所示。

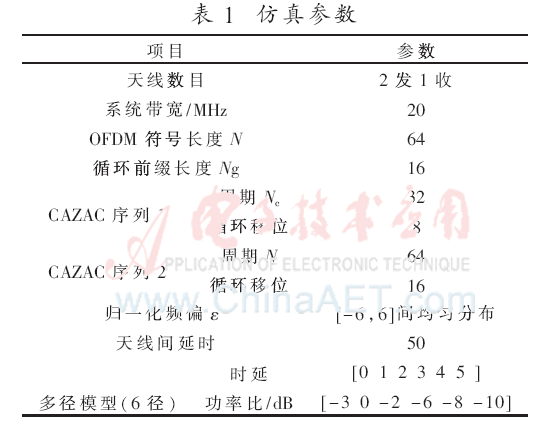
    忽略頻偏影響,，在單徑信道下,，對WPS算法和本文提出算法的正確定時概率進行比較，在不同信噪比下的曲線如圖6所示,?？梢钥闯霰疚奶岢龅乃惴ǘ〞r性能優(yōu)于WPS算法，尤其在低信噪比條件下更為明顯,。

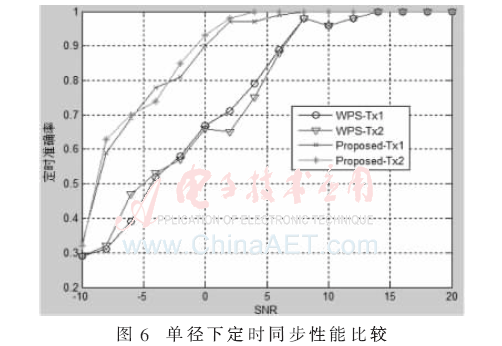
    圖7所示分別為在多徑條件下,，頻偏為0、信噪比為10時,，WPS算法和本文提出算法的定時判決函數曲線,。可以看出,，圖7(a)中WPS算法在兩根發(fā)射天線信號處都能產生峰值,，但是由于偽峰存在，難以判斷定時點的具體位置,；圖7(b),、圖7(c)中，本文提出的算法對兩根發(fā)射天線信號分別進行判斷,，雖然判決函數也存在偽峰,，但是在最強徑定時點上一定取得最大值，偽峰的存在對定時點的判斷并沒有太大影響,。

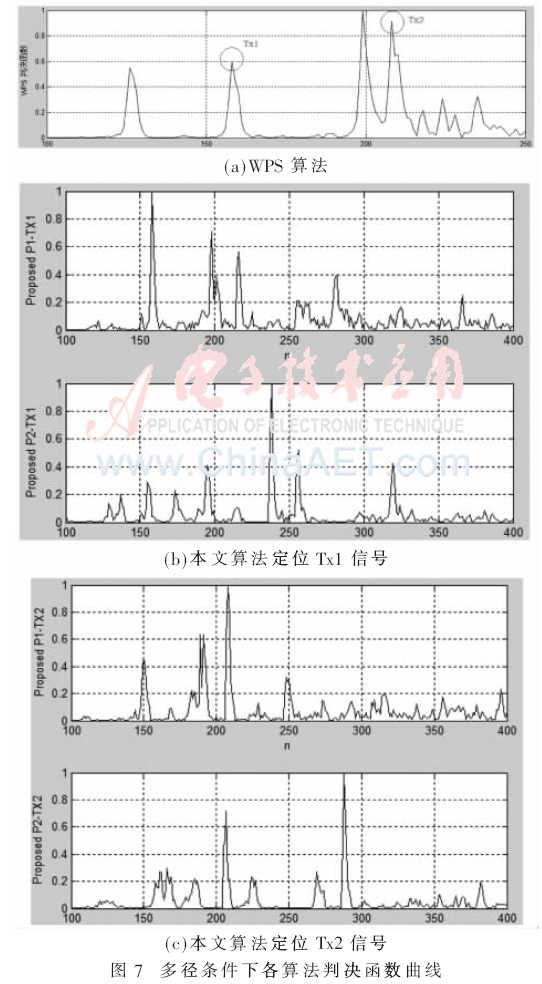
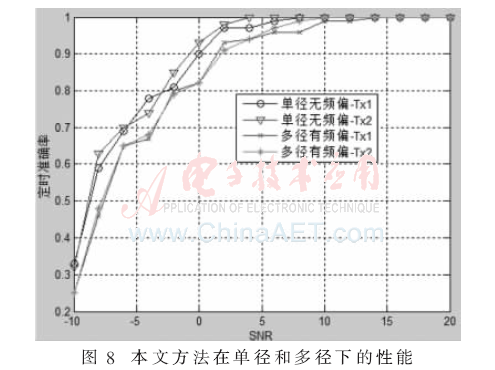
    圖8所示為本文提出方法在單徑無頻偏和多徑有頻偏下的性能對比,。由圖中可以看出，算法在多徑與單徑條件下性能差別不大,，多徑的存在幾乎不對算法性能產生大的影響,，同時也可以看出，算法在有頻偏的情況下也能正確定時,。

4 結束語 

    本文針對MIMO-OFDM系統(tǒng),，提出了一種改進的訓練序列結構和定時同步方法。采用不同長度的CAZAC序列構成訓練序列,，接收時利用本地互相關的方法進行定時同步,。雖然增加了訓練序列的長度，但是能夠直接得出正確的定時點,，使定時位置不受頻偏影響,；并且能同時估計出整數倍頻偏，縮短了同步過程,，從而降低了系統(tǒng)的復雜度,。理論和仿真分析表明,，該方法相對WPS算法有著明顯的性能提升。

參考文獻

[1] CHO YONG SOO,，JAEKWON KIM,，WON YOUNG YANG,，et al.MIMO-OFDM wireless communications with MATLAB[M].John Wiley & Sons,，2010.

[2] RACHINI A，BEYDOUN A,，NOUVEL F,，et al.Timing synchronization method for MIMO-OFDM system using orthogonal preamble[C].Telecommunications(ICT)，2012 19th International Conference on.IEEE,，2012：1-5.

[3] WANG HUNG-CHIN,，WANG CHIN-LIANG.A compact preamble design for synchronization in distributed MIMO OFDM systems[C].IEEE Vehicular Technology Conference(VTC Fall)，San Francisco,，California,，USA：IEEE，2011：1-4.

[4] MODY,，APURVA N,，GORDON L.STUBER.Synchronization for MIMO-OFDM systems[C].Global Telecommunications Conference，2001.GLOBECOM′01.IEEE.San Antonio,，USA：IEEE,，2001：509-513.

[5] SCHMIDL T M，COX D C.Robust frequency and timing synchronization for OFDM[J].Communications,，IEEE Transactions on,，1997，45(12)：1613-1621.

[6] VANZELST V,，SCHENK T C W.Implementation of a MIMO-OFDM-based wireless LAN system[J].Signal Processing,，IEEE Transactions on，2004,，52(2)：483-494.

[7] FENG C,，ZHANG J，ZHANG Y,，et al.A novel timing synchronization method for MIMO OFDM systems[C].Vehicular Technology Conference,，2008.VTC Spring 2008.IEEE.Singapore：IEEE，2008：913-917.

[8] 許成謙,，劉萌萌．多徑衰落信道下MIMO-OFDM系統(tǒng)的定時同步算法[J]．北京郵電大學學報,，2012，35(3)：95-98.

[9] HEIMILLER R C．Phase shift pulse codes with good periodiccorrelation properties[J]．Information Theory,，IRE Transactions on,，1961,，7(4)：254-257.

[10] IEEE Std.802.11nTM-2009[S].IEEE STANDARD for Information Technology-Telecommunications and information exchange between systems-Local and metropolitan area networks-Specific requirements.Oct.2009.