文獻(xiàn)標(biāo)識(shí)碼: A
文章編號(hào): 0258-7998(2015)05-0109-03
0 引言
藝術(shù)家經(jīng)常將圖像、紋理應(yīng)用到三維模型的表面,然而,在模型上顯示圖像時(shí)必須小心,因?yàn)樵诩y理和顯示像素之間沒有一一對(duì)應(yīng)關(guān)系。當(dāng)一個(gè)在遠(yuǎn)處的模型把幾個(gè)紋理對(duì)應(yīng)于每個(gè)像素采樣會(huì)導(dǎo)致錯(cuò)誤的模式,即出現(xiàn)混疊。如果繪制紋理作為二維信號(hào)采樣,香農(nóng)采樣定理要求在圖像采樣之前必須使用一個(gè)低通濾波器去除高頻數(shù)據(jù)。渲染算法通常使用名為Mipmap的圖像金字塔[1]加速圖像濾波。本文提出一種方法,結(jié)合在Mipmap中的紋理重現(xiàn),只讀取每個(gè)樣本的幾個(gè)紋理的低通濾波結(jié)果。由于內(nèi)存帶寬往往是圖形應(yīng)用程序的瓶頸,所以盡可能有效使用帶寬。該方法可以通過擴(kuò)展紋理的數(shù)目來匹配可用帶寬,通過精心選擇紋理元素來準(zhǔn)確地再現(xiàn)圖像過濾器,為圖像的放大、平移和旋轉(zhuǎn)而過濾掉嚴(yán)重的混疊[2]。此方法還可以近似高質(zhì)量的過濾器,例如在實(shí)時(shí)Lanczos 2過濾器[3]中,由于過濾器的尺寸和復(fù)雜性僅僅影響預(yù)處理時(shí)間,因而用來計(jì)算濾波器系數(shù)表和生成Mipmap。
1 多分辨率采樣


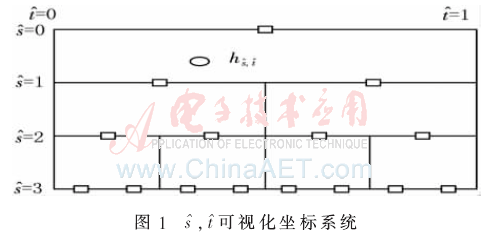


本文的方法和線性插值使用4個(gè)基函數(shù)在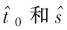 上插值。本文方法的結(jié)果見圖2(a),雙線性插值結(jié)果見圖2(c),從圖上能看出本文方法再現(xiàn)濾波器優(yōu)于線性插值,基函數(shù)乘以系數(shù)用來近似濾波器的結(jié)果顯示在圖2(b)和圖2(d)中。在圖2(b)中不同的平移顯示近似濾波器的最優(yōu)策略取決于參數(shù)
上插值。本文方法的結(jié)果見圖2(a),雙線性插值結(jié)果見圖2(c),從圖上能看出本文方法再現(xiàn)濾波器優(yōu)于線性插值,基函數(shù)乘以系數(shù)用來近似濾波器的結(jié)果顯示在圖2(b)和圖2(d)中。在圖2(b)中不同的平移顯示近似濾波器的最優(yōu)策略取決于參數(shù) 在左邊,最好的方法是從比
在左邊,最好的方法是從比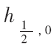 更寬的基函數(shù)中減去;在右邊,最好的解決辦法是增加高分辨率基函數(shù)來近似
更寬的基函數(shù)中減去;在右邊,最好的解決辦法是增加高分辨率基函數(shù)來近似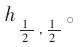
2 多項(xiàng)式擬合

式(4)中cij是二次方程,它作為一個(gè)線性系統(tǒng),可優(yōu)化選擇多少個(gè)紋理可以使用、如何細(xì)分域和多項(xiàng)式的階。
3 組合和啟發(fā)式算法
通過求解線性系統(tǒng)來找到紋理的權(quán)重非常方便,但也會(huì)出現(xiàn)許多紋理集合。對(duì)于每個(gè)子域,需要找到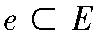 的紋理集合,當(dāng)評(píng)估式(4)時(shí)具有最低的誤差。如果從N=|E|個(gè)可能的紋理中選出n個(gè)紋理,則需要檢查
的紋理集合,當(dāng)評(píng)估式(4)時(shí)具有最低的誤差。如果從N=|E|個(gè)可能的紋理中選出n個(gè)紋理,則需要檢查 個(gè)紋理組合的錯(cuò)誤。顯然,為容易處理這個(gè)問題需要盡可能地減小N。首先需要觀察的是排除紋理不在
個(gè)紋理組合的錯(cuò)誤。顯然,為容易處理這個(gè)問題需要盡可能地減小N。首先需要觀察的是排除紋理不在 的支持內(nèi),其次需要觀察的是當(dāng)n很小時(shí)主要用低分辨率紋理來近似濾波器。對(duì)于一個(gè)n=8的濾波器僅用來自相對(duì)于Mipmap的0、1和2級(jí)的紋理,因此在優(yōu)化過程中可以排除其他的分辨率。
的支持內(nèi),其次需要觀察的是當(dāng)n很小時(shí)主要用低分辨率紋理來近似濾波器。對(duì)于一個(gè)n=8的濾波器僅用來自相對(duì)于Mipmap的0、1和2級(jí)的紋理,因此在優(yōu)化過程中可以排除其他的分辨率。
4 實(shí)現(xiàn)

圖3中用曲線圖表示本文方法的近似誤差和三線性插值的誤差歸一化,比較一個(gè)直接卷積濾波器為從2~10的整數(shù)樣本。本文方法的成本取決于子域的數(shù)目和匹配多項(xiàng)式的順序,所以比較線性多項(xiàng)式為ei在2×2×1、4×4×2和8×8×4細(xì)分域上的誤差以及二次多項(xiàng)式在2×2×1和4×4×2細(xì)分域上的誤差。本文的方法可以近似各種濾波器,用不同濾波器進(jìn)行Mipmap采樣時(shí),比較本文方法與三線性插值的誤差。
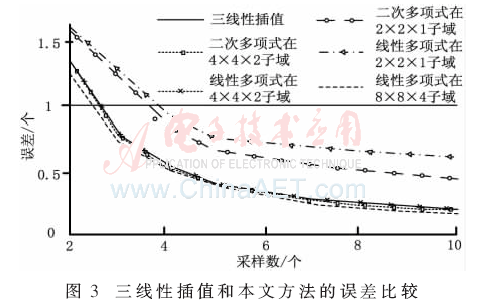
圖4是使用8個(gè)紋理的濾波器來展示本文方法的訪問模式的示例。從3個(gè)Mipmap級(jí)別讀取,而三線性插值僅僅從2個(gè)級(jí)別讀取,通過使用兩個(gè)緩存交替Mipmap級(jí)別為三線性訪問作GPU優(yōu)化,從3個(gè)級(jí)別讀取會(huì)導(dǎo)致緩存沖突。圖形處理器也可能通過三線性插值優(yōu)化2×2四邊形紋理。本文方法也將不規(guī)則地讀取相鄰像素,因?yàn)樵谝粋€(gè)4×4×2離散相鄰的像素中將至少有一個(gè)子域的跨越。
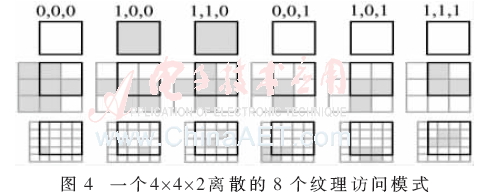
測(cè)試在ATI和NVIDIA的GPU之間是一致的,表明了本地硬件實(shí)現(xiàn)顯著提高了三線性插值的性能,展示了一個(gè)濾波器的4×4×2離散的8個(gè)紋理訪問模式。單元域?yàn)榇志€條黑色方框,圖像的每一列表示在一個(gè)子域所使用的紋理,其中具有非零系數(shù)的紋理為黑色陰影。
圖5為使用一個(gè)濾波器,取4、6和8個(gè)紋理元件時(shí)表現(xiàn)出鋸齒在一個(gè)無限平面的棋盤圖案。一個(gè)差的過濾器不能輕松地隱藏混疊模式,當(dāng)使用8個(gè)紋理、在三線性插值獲取相同數(shù)目的紋理時(shí),本文的過濾器看起來銳利和清晰;使用6個(gè)紋理和8個(gè)紋理的結(jié)果幾乎無區(qū)別;當(dāng)使用4個(gè)紋理元素,圖像會(huì)略顯雜亂,并在前臺(tái)邊緣顯得有點(diǎn)粗糙。

5 結(jié)論
內(nèi)存帶寬是圖形應(yīng)用的一個(gè)瓶頸,本文方法具有一定的實(shí)用價(jià)值,其局限是GPU已設(shè)計(jì)為三線性插值優(yōu)化,這使得多種解釋方法可能存在:一個(gè)是該方法更適合于離線光柵化和光線追蹤;另一個(gè)是硬件設(shè)計(jì)將改變以更好地支持隨機(jī)訪問該方法的訪問模式。實(shí)驗(yàn)表明,在簡單的假設(shè)下可以通過優(yōu)化紋理和系數(shù)實(shí)現(xiàn)更好的濾波。
參考文獻(xiàn)
[1] WILLIAMS L.Pyramidal parametrics[M].SIGGRAPH,1983:1-11.
[2] 吳江波,汪西原.一種改進(jìn)的基于紋理和顏色的運(yùn)動(dòng)陰影檢測(cè)[J].電視技術(shù),2014,38(7):178-181.
[3] DUCHON C.Lanczos filtering in one and two dimensions[J].Journal of Applied Meteorology,1979,18(8):1016-1022.
[4] 李國成,肖慶憲.基數(shù)約束投資組合問題的一種混合元啟發(fā)式算法求解[J].計(jì)算機(jī)應(yīng)用研究,2013,30(8):2292-2297.
[5] 王波,高岳林.基數(shù)約束下基于CVaR度量的投資組合優(yōu)化模型[J].統(tǒng)計(jì)與決策,2011,14(1):52-55.

