文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2014)09-0130-03
隨著汽車電子技術(shù)的飛速發(fā)展,國內(nèi)外眾多學(xué)者對智能車輛視覺導(dǎo)航系統(tǒng)進(jìn)行了深入的研究。由于智能車輛視覺導(dǎo)航橫向控制系統(tǒng)在實(shí)際運(yùn)行中將會受到車輛參數(shù)的影響,采用何種適宜的橫向控制策略是當(dāng)前研究的熱點(diǎn)[1]。國內(nèi)外關(guān)于橫向控制策略的研究主要集中在以下方面:參考文獻(xiàn)[2]以車輛與路徑上近點(diǎn)作為基準(zhǔn)點(diǎn),結(jié)合自適應(yīng)PID算法和模糊控制方法,由于對前方環(huán)境缺乏預(yù)見性而限制了系統(tǒng)的控制有效性和準(zhǔn)確性;參考文獻(xiàn)[3]基于汽車操縱動力學(xué)模型建立了智能車輛自主導(dǎo)航最優(yōu)控制模型,該模型非常適用于低速行駛車輛,取得了較好的控制效果,但是在智能車輛高速行駛過程中控制效果較差;參考文獻(xiàn)[4]將轉(zhuǎn)向盤轉(zhuǎn)矩作為主導(dǎo)控制參數(shù),建立了一個魯棒控制模型,由于轉(zhuǎn)向盤轉(zhuǎn)矩與駕駛?cè)说牟倏v行為過程密切相關(guān),但是該模型并未將駕駛?cè)诵袨槟P图{入考慮范疇;參考文獻(xiàn)[5]采用直接橫擺力矩控制策略進(jìn)行車輛橫向控制,但該控制策略受預(yù)瞄點(diǎn)選擇的影響較大,導(dǎo)致控制效果差異性大;參考文獻(xiàn)[6]建立了駕駛?cè)祟A(yù)瞄行為模型,并結(jié)合專家先驗(yàn)知識預(yù)測、預(yù)瞄距離實(shí)現(xiàn)對智能車輛的橫向控制,但是在預(yù)瞄控制模型中僅將車輛速度簡單劃分為快、中、慢3個范圍,導(dǎo)致系統(tǒng)的可靠性和適應(yīng)性較差。
為了大幅提高智能車輛視覺導(dǎo)航過程中橫向控制的精度,進(jìn)一步減少路徑彎度、預(yù)瞄距離等因素的影響,本文建立了橫擺角速度預(yù)測模型、車輛7自由度操縱動力學(xué)模型,結(jié)合系統(tǒng)辨識的方法,提出了一種橫擺角速度與橫向偏差的智能車輛橫向模糊控制策略。仿真結(jié)果驗(yàn)證了本文所提出的智能車輛視覺導(dǎo)航橫向模糊控制策略的有效性和良好的適應(yīng)性。
1 控制系統(tǒng)結(jié)構(gòu)設(shè)計[7]
智能車輛視覺導(dǎo)航橫向模糊控制策略如圖1所示。根據(jù)空間幾何坐標(biāo)系逆透視投影轉(zhuǎn)換得到的車輛預(yù)瞄點(diǎn)的相對位置,建立橫擺角速度預(yù)測模型以及7自由度車輛操縱動力學(xué)模型。模糊控制系統(tǒng)的設(shè)計中非常關(guān)鍵的環(huán)節(jié)即模糊控制器的輸入變量的選擇,在智能車輛視覺導(dǎo)航過程中,車身橫向運(yùn)動的控制本質(zhì)上即動態(tài)調(diào)整車輛相對于行駛路徑的橫向偏差和航向偏差這兩個運(yùn)動參數(shù)。綜上可知,車輛實(shí)時位姿信息必須作為重點(diǎn)考慮的因素,因此本文將車輛的橫擺角速度和橫向偏差作為模糊控制器的兩個輸入項。

2 橫擺角速度預(yù)測模型的建立[8]
假設(shè)在某一特定時刻,世界坐標(biāo)系中的車輛質(zhì)心坐標(biāo)為(Xw,Yw),車輛坐標(biāo)系的縱軸線與橫坐標(biāo)之間的夾角為φv。已知車輛質(zhì)心速度v、車輛質(zhì)心側(cè)偏角β以及車輛橫擺角速度ω,則車輛動力學(xué)方程可以用下式表示:

通過式(1)不難看出,智能車輛視覺導(dǎo)航中的車身位置姿態(tài)與車輛橫擺角速度、車輛質(zhì)心速度、質(zhì)心側(cè)偏角這3個因素密切相關(guān)。在諸多因素之中,車輛橫擺角速度的變化對車輛的軌跡狀態(tài)影響較大。因此可以在利用車輛質(zhì)心速度變化率的基礎(chǔ)上,通過控制車輛的橫擺角速度進(jìn)一步干涉智能車輛的運(yùn)動狀態(tài)。
在建立橫擺角速度預(yù)測模型的過程中,為了進(jìn)一步提高系統(tǒng)的控制效果,忽略車輛運(yùn)動中的質(zhì)心偏差,并假設(shè)車輛一直沿視覺導(dǎo)航路徑行駛,運(yùn)動軌跡保持不變,不發(fā)生突變,則橫擺角速度可以通過下式表示:

3 車輛操縱動力學(xué)模型的建立
通過對車輛操縱動力學(xué)的研究分析以及根據(jù)智能車輛視覺導(dǎo)航過程中橫向控制策略仿真研究的實(shí)際需要,本文建立了一個包括橫擺、側(cè)傾、俯仰3個自由度以及車輪4個自由度的7自由度車輛操縱動力學(xué)模型[9],如圖2所示。


4 模糊控制模型的建立
本文建立了智能車輛橫向模糊控制器,其中兩個輸入變量中,將橫擺角速度e的模糊論域定義為[-3,3],橫向偏差ec的模糊論域定義為[-3,3]。其輸入變量的論域都劃分成7個模糊子集用NB、NM、NS、ZE、PS、PM、PB表示,輸出控制變量k的論域設(shè)為[-0.06,0.06],并把它劃分為7個模糊子集(即NB、NM、NS、ZE、PS、PM、PB),模糊子集中對應(yīng)的元素分別表示負(fù)大、負(fù)中、負(fù)小、零、正小、正中、正大。在完成了模糊論域和模糊子集的參數(shù)化過程之后,需要進(jìn)一步確定模糊論域內(nèi)所包含的元素對模糊變量的隸屬度函數(shù)。如圖3~圖5所示分別為橫擺角速度e、橫向偏差ec以及控制變量k的隸屬度函數(shù)[10]。
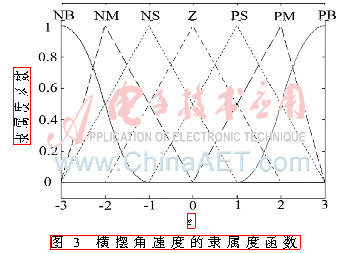
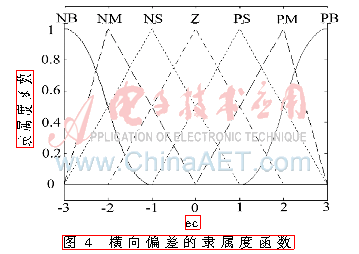
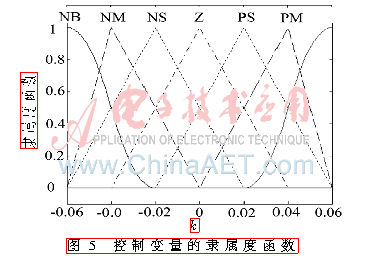
綜合考慮智能車輛視覺導(dǎo)航橫向控制系統(tǒng)的應(yīng)用特點(diǎn),如表1所示,本文建立了系統(tǒng)輸出控制變量k的模糊控制規(guī)則表。

模糊邏輯推理作為模糊控制的核心內(nèi)容,用來確定控制參數(shù)的模糊向量。本文中采用了模糊控制中普遍使用的Mamdani推理法,它根據(jù)模糊控制算法和規(guī)則計算出最終控制量。反模糊化過程采用工業(yè)控制中普遍采用的重心法,以獲取較為滿意的推理控制結(jié)果[11]。
5 系統(tǒng)模糊控制策略仿真分析
為了檢驗(yàn)本文所提出的控制策略的有效性和可靠性,以MATLAB/Simmulink作為仿真環(huán)境,建立了智能車輛視覺導(dǎo)航中的橫向模糊控制模型,并對其進(jìn)行了仿真實(shí)驗(yàn),如表2所示為控制系統(tǒng)的部分仿真參數(shù)。假設(shè)車輛分別以30 km/h和70 km/h的車速行駛,設(shè)置虛擬路徑作為模擬仿真的行駛路徑,仿真模擬結(jié)果分別如圖6~圖9所示。


如圖6所示為車輛行駛軌跡對比曲線,從圖中可以看出,采用橫向模糊控制策略控制精度更高,進(jìn)一步減小了車輛與最近點(diǎn)之間的距離偏差,在常規(guī)路況控制中均能穩(wěn)定地沿目標(biāo)路徑行駛,具有良好的跟蹤特性。如圖7所示為車輛橫擺角速度對比曲線,與不加任何控制策略的橫擺角速度曲線相比較,采用橫向模糊控制策略進(jìn)一步降低了系統(tǒng)的響應(yīng)時間和減小了響應(yīng)峰值,獲得了更加優(yōu)化的動態(tài)控制性能,能夠滿足系統(tǒng)控制穩(wěn)定性的需求。
圖8和圖9分別為車輛低速和高速行駛過程中出現(xiàn)的橫向偏差。通常情況下隨著車輛縱向速度的增加,其橫擺運(yùn)動會出現(xiàn)較大幅度的變化,然而仿真結(jié)果表明,采用橫向模糊控制策略車輛橫向加速度增大幅度并不明顯,在縱向速度有較大增加時,智能車輛趨向行車路線所需的時間只是出現(xiàn)略微增加,當(dāng)然實(shí)際行駛的距離肯定會有明顯增加,但并未對車輛橫向控制帶來不便,最終可以提高智能車輛對縱向速度的快速適應(yīng)能力,從而獲得更好的橫向運(yùn)動穩(wěn)定性和易操控性。
因此,采用本文提出的基于橫擺角速度與橫向偏差的智能車輛橫向模糊控制策略,使得智能車輛橫向位移控制精度有顯著提高。同時對縱向速度具有較好的適應(yīng)能力,取得了非常好的效果,橫向偏差誤差范圍較小,具有較好的穩(wěn)定性和適應(yīng)性。
本文通過對智能車輛視覺導(dǎo)航中橫向控制特點(diǎn)的深入分析,針對目前橫向控制策略存在的問題,提出了一種基于橫擺角速度與橫向加速度的智能車輛視覺導(dǎo)航橫向模糊控制策略,并建立了7自由度車輛操縱動力學(xué)模型,最后進(jìn)行了仿真實(shí)驗(yàn)驗(yàn)證。仿真結(jié)果表明,本文采取的控制策略不僅較好地滿足了車輛橫向控制平穩(wěn)性和舒適性要求,并且對車輛縱向速度具有令人滿意的適應(yīng)能力,具有廣泛的應(yīng)用前景和實(shí)際意義。
參考文獻(xiàn)
[1] 馬瑩,王建強(qiáng),徐友春,等.智能車輛車道保持系統(tǒng)[J].ITS通訊,2004,19(1):7-12.
[2] 王京起,陳慧巖,鄭培.應(yīng)用模糊自適應(yīng)PID和預(yù)瞄策略的自主車輛轉(zhuǎn)向控制[J].汽車工程,2003,25(4):367-371.
[3] 王榮本,李兵,徐友春.基于視覺的智能車輛自主導(dǎo)航最優(yōu)控制器設(shè)計[J].汽車工程,2001,23(2):97-100.
[4] MASAYASU S,HIROSHI K,ON S,et al.Design of lanekeeping control with steering torque input for a lane-keeping support system[R].SAE,2001-01-0480,2001.
[5] PONGSATHORN R,MASAO N,MOTOKI S.Lane keeping control strategy with direct yaw moment control input by considering dynamics of electric vehicle[J].Vehicle System Dynamics,2006(44):192-201.
[6] YANAGIYA M,TOMITA K,TSUGAWA S.Effects of field of view on lateral control performance in a vision-based autonomous vehicle[J].JSAE Review,1999,20(4):499-504.
[7] 丁海濤,郭孔輝,李飛,等.基于加速度反饋的任意道路和車速跟隨控制駕駛員模型[J].機(jī)械工程學(xué)報,2010,46(10):116-120.
[8] 李小勇,張文濤,熊顯名.基于車輛視覺的車道閘桿防撞系統(tǒng)研究[J].微型機(jī)與應(yīng)用,2014,33(1):40-45.
[9] 王家恩,陳無畏,王檀彬,等.基于期望橫擺角速度的視覺導(dǎo)航智能車輛橫向控制[J].機(jī)械工程學(xué)報,2012,48(4):107-114.
[10] 郭孔輝.汽車操縱動力學(xué)[M].長春:吉林科學(xué)技術(shù)出版社,1991.
[11] 劉金琨.智能控制[M].北京:清華大學(xué)出版社,2005.

