2 系統(tǒng)分析與設(shè)計(jì)
首先根據(jù)需要選取產(chǎn)生混沌信號(hào)的混沌方程。然后確定方程的系數(shù)及初值。與采用分立元件設(shè)計(jì)信號(hào)源不同的是:分立元件設(shè)計(jì)混沌信號(hào)源的系數(shù)是需要通過(guò)電路結(jié)構(gòu)分析計(jì)算各元件的參數(shù)值得到,而采用DSP設(shè)計(jì)信號(hào)源直接設(shè)定即可;分立元件設(shè)計(jì)混沌信號(hào)源時(shí)不必設(shè)定初值,而采用DSP設(shè)計(jì)混沌信號(hào)源時(shí)方程的初值設(shè)定是必不可少的。初值可以是不為零的任意數(shù),但最好選取在混沌系統(tǒng)的吸引子中,這樣能使系統(tǒng)迅速進(jìn)入混沌。因?yàn)镈SP產(chǎn)生的混沌信號(hào)極其有限,可根據(jù)實(shí)際需要在輸出端采用其他電路設(shè)計(jì)增益放大電路。圖1為系統(tǒng)設(shè)計(jì)流程。
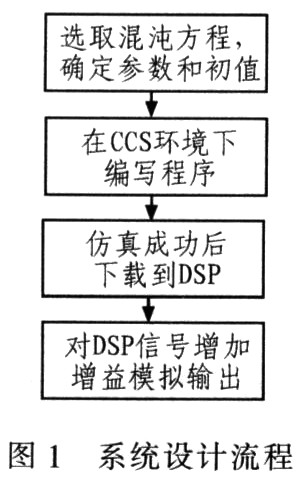
3 程序設(shè)計(jì)和精度問(wèn)題
3.1 程序設(shè)計(jì)
此設(shè)計(jì)中的DSP主要用于微分?jǐn)?shù)值的迭代運(yùn)算,其計(jì)算性能將決定信號(hào)產(chǎn)生速度,這里采用TI公司的TMS320C5402型低功率器件作為核心,其速度可達(dá)100 MI/s,以Lorenz方程為例,其方程如下:
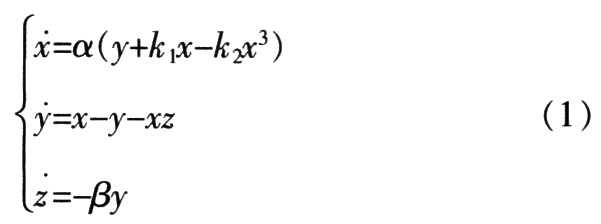
式中,參數(shù)值分別為:α=5.5,β=-7.4,k1=0.25,k2=0.1。
圖2為系統(tǒng)程序流程。


3.2 精度問(wèn)題
混沌信號(hào)的產(chǎn)生主要借助于:DSP強(qiáng)大的運(yùn)算能力,采用數(shù)值計(jì)算方法,可根據(jù)不同的精度要求選用不同的方法。精度越高,運(yùn)算量越大,則混沌信號(hào)的頻率越低,所以要根據(jù)實(shí)際需要選取合適的精度。混沌方程的微分?jǐn)?shù)值計(jì)算方法主要有:歐拉方法、改進(jìn)歐拉方法及四階龍格一庫(kù)塔法。這3種方法精度由低到高,計(jì)算量也由低到高。運(yùn)算量的大小直接決定運(yùn)算速度,即決定混沌信號(hào)的產(chǎn)生速度。選用何種計(jì)算方法取決于對(duì)精度和速率的要求以及對(duì)運(yùn)算量的承受能力。上述核心程序采用四階龍格一庫(kù)塔法。
4 信號(hào)的驗(yàn)證與測(cè)試
4.1 信號(hào)驗(yàn)證
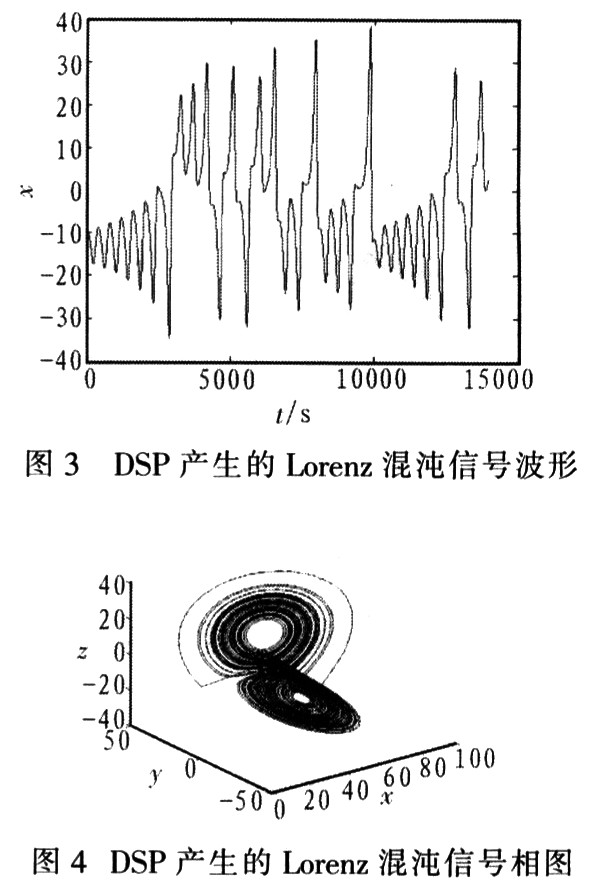
產(chǎn)生的信號(hào)是否為混沌信號(hào)必須經(jīng)過(guò)驗(yàn)證。判斷混沌信號(hào)的方法很多,但都存在需要復(fù)雜運(yùn)算的問(wèn)題。一般情況下通過(guò)示波器顯示的單通道波形很難判斷混沌與否。MATLAB和TI公司聯(lián)合開發(fā)的MATLAB Link for CCS Development Tool(簡(jiǎn)稱CCSlink)工具箱更適合于程序的調(diào)試,對(duì)混沌信號(hào)的驗(yàn)證不夠靈活。這里采用一種簡(jiǎn)單有效的方法判斷DSP產(chǎn)生的信號(hào)是否混沌。運(yùn)用 JTAG測(cè)試技術(shù)和CCS的在線調(diào)試功能,直接訪問(wèn)DSP內(nèi)存。以Lorenz混沌信號(hào)的檢測(cè)為例,在CCS編譯環(huán)境的程序部分通過(guò)設(shè)定,將數(shù)據(jù)X存在 DSP的地址0X0088,Y存在地址0X0099,Z存在地址0X00A0,使用探針功能采集內(nèi)存中的數(shù)據(jù),并將其存為DAT文件格式,然后利用 Matlab強(qiáng)大的圖形能力對(duì)數(shù)據(jù)進(jìn)行處理,通過(guò)分析相圖判斷信號(hào)是否為混沌信號(hào)。這里共采集98 047個(gè)點(diǎn)的數(shù)據(jù)。利用Matlab方法將采集到的DSP產(chǎn)生的數(shù)據(jù)制成波形圖和相圖,分別如圖3、圖4所示。由圖3和圖4易知產(chǎn)生的數(shù)據(jù)是混沌的,從而驗(yàn)證了設(shè)計(jì)的正確性。
4.2 可重用性測(cè)試
為驗(yàn)證系統(tǒng)的可通用性,對(duì)Lorenz混沌信號(hào)產(chǎn)生模塊稍作修改,修改的內(nèi)容包括:微分方程、參數(shù)值以及初始值。
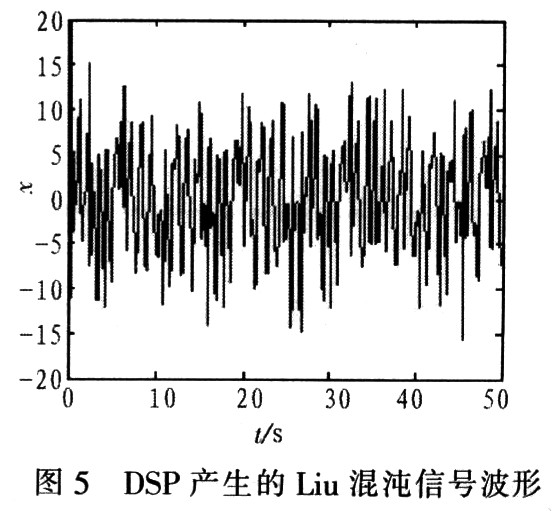
Liu系統(tǒng)的方程為:

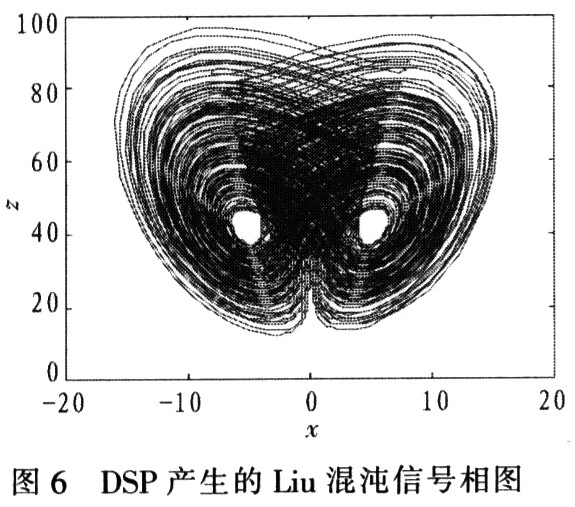
采用同樣的方法,得到Liu系統(tǒng)產(chǎn)生的混沌信號(hào)。如圖5和圖6所示。
5 結(jié)論
針對(duì)模擬電路設(shè)計(jì)的混沌信號(hào)模塊結(jié)構(gòu)復(fù)雜、噪聲高等缺點(diǎn),采用DSP實(shí)現(xiàn)了可調(diào)精度的混沌信號(hào)產(chǎn)生模塊,并實(shí)現(xiàn)了Lorenz方程和Liu系統(tǒng)的混沌信號(hào)。總結(jié)如下:以TI公司的TMS320C5402型DSP為例給出了混沌信號(hào)源詳細(xì)的設(shè)計(jì)方法,并對(duì)信號(hào)進(jìn)行了驗(yàn)證;運(yùn)用JTAG測(cè)試技術(shù)和CCS的在線調(diào)試,直接訪問(wèn)DSP內(nèi)存,進(jìn)而判斷信號(hào)是否發(fā)生混沌,此方法簡(jiǎn)單有效。該模塊的設(shè)計(jì)可根據(jù)不同應(yīng)用需求,如對(duì)混沌信號(hào)產(chǎn)生速率、功耗、精度等方面的要求,選擇不同器件片。所以具有很大的通用性和靈活性。

