摘  要： 提出了一種針對基于標(biāo)量乘的公鑰密碼體制的攻擊方法,。由于小整數(shù)n階點(diǎn)在點(diǎn)加和倍點(diǎn)運(yùn)算時能夠產(chǎn)生顯著數(shù)值變化,，即產(chǎn)生顯著功耗變化,，因此基于小整數(shù)n階點(diǎn)的選擇明文與簡單功耗分析可以有效攻擊橢圓曲線密碼(ECC)這種基于標(biāo)量乘的公鑰密碼算法。
關(guān)鍵詞： 橢圓曲線密碼,；簡單功耗分析,；標(biāo)量乘

    與對稱密鑰密碼體系相比，公鑰密碼體系允許更靈活的密鑰管理,。目前,，應(yīng)用最廣泛的兩種公鑰密碼算法是RSA以及橢圓曲線密碼(ECC)算法[1-2]。與RSA相比,，ECC具有更短的密鑰長度,、更快的運(yùn)算(諸如內(nèi)存、能量消耗以及帶寬存儲),，從而在學(xué)術(shù)與工程領(lǐng)域引起持續(xù)增長的興趣,。
    側(cè)信道分析(如時序、功耗,、電磁輻射)攻擊已經(jīng)對公鑰密碼體制的硬件實(shí)現(xiàn)產(chǎn)生了威脅,。簡單功耗分析SPA(Simple Power Analysis)攻擊已被證明可有效攻擊一些公鑰密碼算法[3]。該技術(shù)主要涉及對運(yùn)行公鑰加密算法的設(shè)備功耗進(jìn)行檢查分析,。RSA實(shí)現(xiàn)中的模方和模乘運(yùn)算是可以被區(qū)分開的,，使得對方可以獲得密鑰。ECC中點(diǎn)加和倍點(diǎn)操作類似于RSA中的模方和模乘操作,。如果可以區(qū)分ECC實(shí)現(xiàn)中的點(diǎn)加和倍點(diǎn)操作,，那么攻擊者就可以獲取ECC密鑰,。
    目前大多數(shù)的RSA算法都使用相同的序列進(jìn)行模乘和模方操作,，大多數(shù)ECC算法也使用相同的序列進(jìn)行點(diǎn)加和倍點(diǎn)運(yùn)算，這增大了對差異的區(qū)分難度,。RSA中“一貫的模乘和模方操作”以及ECC中“一貫的點(diǎn)加和倍點(diǎn)操作”似乎成為了對抗SPA攻擊的有效手段,。為了從功耗波形中獲得更強(qiáng)的信息泄露，針對特殊輸入數(shù)據(jù)的RSA的選擇明文攻擊方法得以提出[4-7],，以及采取更為復(fù)雜的原子化平衡操作[9]和蒙哥馬利方法[10]等,，但都使得在SPA攻擊時得不到點(diǎn)加和倍點(diǎn)運(yùn)算的顯著功耗變化。
    為了在功耗波形中獲得增強(qiáng)的信息泄露,，本文提出了一種針對ECC算法的選擇明文側(cè)信道攻擊方法,，該方法利用了2階或者其他小整數(shù)階點(diǎn)作為特殊輸入點(diǎn)P，以增強(qiáng)點(diǎn)和倍點(diǎn)操作中的顯著變化,。
1 ECC概述
1.1 橢圓曲線
    ECC算法把現(xiàn)有的離散對數(shù)問題轉(zhuǎn)化為橢圓曲線上的連續(xù)問題,。一個生成元為g的n階循環(huán)群G的離散對數(shù)問題指的是找出群G上使y=gx成立的x。橢圓曲線上的離散對數(shù)比其他有限域上的群(諸如乘法群)要困難得多,。令E(EP)為一個定義在有限域FP上的橢圓曲線,，令P為一個E(EP)上的點(diǎn),。素?cái)?shù)p、橢圓曲線方程FP,、點(diǎn)P以及其階數(shù)n是公共的域參數(shù),。私鑰是一個從區(qū)間[1，n-1]上均勻隨機(jī)選取的整數(shù)d,，其相應(yīng)的公鑰是Q=dP,。私鑰d的確定問題就是橢圓曲線上的離散對數(shù)問題(ECDLP)。
   

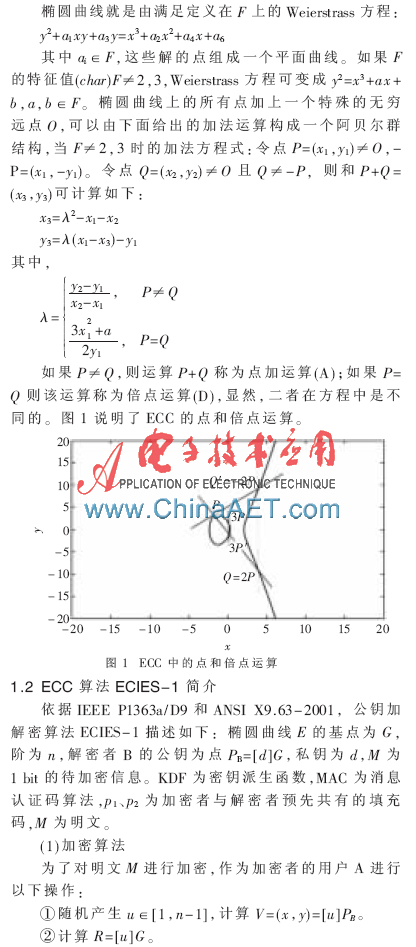
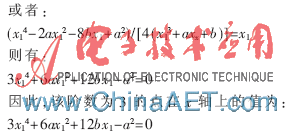
    尋找其他階數(shù)點(diǎn)的方法可以進(jìn)一步閱讀參考文獻(xiàn)[10-12],。
    本文提出了一種新的選擇明文的簡單功耗分析攻擊法,。在該方法中，選擇階數(shù)為2或者其他小整數(shù)階點(diǎn)作為特殊點(diǎn)P,，是為了利用其在無限域上的特殊性,。該方法放大了點(diǎn)倍與點(diǎn)加操作的功耗差。通過該方法,，可以對ECC實(shí)現(xiàn)中的從左至右或從右至左二進(jìn)制算法進(jìn)行有效攻擊,。
參考文獻(xiàn)
[1] MILLER V S.Use of elliptic curves in cryptography[C]. Advances in Cryptology，CRYPTO’85 Proceedings,，1986,，218：417-426.
[2] KOBLITZ N.Elliptic curve cryptosystems[J].Mathematics of Computation，1987,，48(177)：203-209.
[3] KOCHER P,，JAFFE J，JUN B.Timing attacks on implementations of Diffie-Hellman,，RSA,，DSS，and other systems[C]. Proceedings of 16th International Advances in Cryptology  Conference,，CRYPTO’96,，1996，1109：104-113.
[4] MIYAMOTO A,，HOMMA N,，AOKI T，et al.Enhanced power analysis attack using chosen message against RSA hardware implementations[C].IEEE Intrnational Symposium on Circuits  and Systems,，ISCAS 2008,，2008：3282-3285.
[5] NOVAK R.SPA-based adaptive chosen-ciphertext attack on RSA implementation[C].International Workshop on Practice and Theory in Public Key Cryptography，LNCS,，2002,，2274：252-262.
[6] BOER B D，LEMKE K,，WICKE G.A DPA attack against  the modular reduction within a CRT implementation of RSA[C]. International Workshop on Cryptographic Hardware and Embedded Systems,，CHES 2002,，LNCS，2003,，2523：228-243.
[7] YEN S M,，LIEN W C，MOON S J,，et al.Power analysis by exploiting chosen message and internal collisions-vulnerability of checking mechanism for RSA-decryption[J].Proceedings of Progress in Cryptology,，Mycrypt 2005，2005,，3715：183-195.
[8] Chen Tingding,，Li Huiyun，Wu Keke,，et al.Countermeasure of ECC against side-channel attacks：balanced point addition and point doubling operation procedure[C].Asia-Pacific Conference on Information Processing,APCIP 2009,，2009，2:465-469.
[9] KIHARA S.On the rank of elliptic curves with a rational point of order 4[J].Proceedings of the Japan Academy,，Series A,，Mathematical Sciences，2004,，80(4)：21-34.
[10] KIHARA S.On the rank of elliptic curves with three rational points of order 2.Ⅲ[J].Proceedings of the Japan Academy,，Series A，Mathematical Sciences,，2004,，80(3)：13-20.
[11] KIHARA S. On the rank of elliptic curves with a rational point of order 4.Ⅱ[J].Proceedings of the Japan Academy,Series A，Mathematical Sciences,，2004,，80(8)：151-168.
[12] Li Huiyun，Wu Keke,，Xu Guoqing,，et al.Simple power analysis attacks using chosen message against ECC hardware implementations[C].World Congress on Internet Security, 2011:68-72.