摘  要： 在自適應(yīng)遺傳算法的基礎(chǔ)上,，提出了一種基于模板匹配的測量固態(tài)流體速度的方法,。基于基本遺傳算法的模板匹配快速,、簡單且魯棒性好[6],，但準(zhǔn)確度不夠，因此采用改進(jìn)的自適應(yīng)遺傳算法,。實(shí)驗(yàn)證明,，基于自適應(yīng)遺傳算法的模板匹配高效準(zhǔn)確，能夠滿足所采取的嵌入式實(shí)驗(yàn)平臺(tái)關(guān)于實(shí)時(shí)性,、準(zhǔn)確性的基本要求,。
關(guān)鍵詞：自適應(yīng)遺傳算法,；模板匹配；嵌入式

    遺傳算法是模仿自然界生物進(jìn)化機(jī)制發(fā)展起來的隨機(jī)全局搜索和優(yōu)化方法,，它借鑒了達(dá)爾文的進(jìn)化論和孟德斯鳩的遺傳學(xué)說,具有簡單,、快速及魯棒性好等特點(diǎn),在函數(shù)優(yōu)化、組合優(yōu)化,、生產(chǎn)調(diào)度,、自動(dòng)控制、機(jī)器人學(xué),、圖像處理和遺傳編程等領(lǐng)域得到廣泛應(yīng)用[1],。本文利用它在圖像匹配方面的應(yīng)用，來實(shí)現(xiàn)已知時(shí)間差之間固態(tài)流體圖像中的圖像模板匹配,，從而實(shí)現(xiàn)對固態(tài)流體的測速,。針對簡單遺傳算法容易產(chǎn)生“早熟”現(xiàn)象、局部尋優(yōu)能力較差和收斂速度慢等缺點(diǎn),，本文將自適應(yīng)遺傳算法引入模板匹配其中,，從而實(shí)現(xiàn)快速準(zhǔn)確的模板匹配,滿足了固態(tài)流體流速檢測關(guān)于實(shí)時(shí)性準(zhǔn)確性的要求。
1自適應(yīng)遺傳算法的原理和流程
1.1基本遺傳算法
    基本遺傳算法的原理和步驟如下,。先將解空間中的解數(shù)據(jù)通過編碼(encode)操作,，完成表現(xiàn)型到基因型的映射。然后以隨機(jī)的方式產(chǎn)生一個(gè)初始化群體（population）,，對其中的個(gè)體進(jìn)行適應(yīng)度的評價(jià)檢測,，再經(jīng)過選擇（selection）、交叉（crossover）和變異（mutation）操作產(chǎn)生下一代的群體,。對新一代群體重復(fù)上述適應(yīng)度評價(jià),、選擇、交叉和變異操作,，直到達(dá)到預(yù)先設(shè)定的進(jìn)化代數(shù)[2],。在最后一代中選出最大適應(yīng)度的個(gè)體，對其進(jìn)行解碼（decode）之后得到最優(yōu)解,。
    基本遺傳算法存在以下不足：在基本遺傳算法(SGA)參數(shù)中,， 交叉率(PC)和變異率(Pm)直接影響算法的收斂速度。交叉率的大小決定新個(gè)體產(chǎn)生速度的快慢,交叉率越大,舊個(gè)體的模式越容易被破壞,新個(gè)體產(chǎn)生的速度就越快,。過高的交叉率可能使較優(yōu)良的個(gè)體的模式遭到破壞,過小的交叉率又會(huì)延緩新個(gè)體的產(chǎn)生,導(dǎo)致算法早熟,停滯不前,。變異率是決定算法跳出局部最優(yōu)解的一個(gè)關(guān)鍵因素,變異率過小，不易生成新的模式結(jié)構(gòu);而變異率過大,，會(huì)使SGA成為純粹的隨機(jī)搜索算法,。基本遺傳算法采用固定的交叉率和變異率,，不能使適應(yīng)度高的個(gè)體有較小的PC和Pm以保留其優(yōu)良基因,，也不能使低劣個(gè)體(適應(yīng)度低的個(gè)體)有較小的PC和Pm以加快其進(jìn)化速度。SGA的這一缺陷導(dǎo)致在處理優(yōu)化問題時(shí)收斂速度慢,，也容易產(chǎn)生“早熟”現(xiàn)象,陷入局部最優(yōu)解[2],。


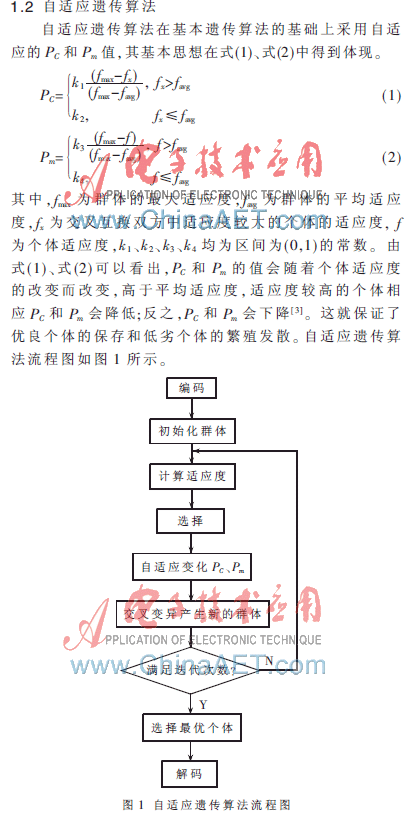
2 自適應(yīng)遺傳算法在模板匹配中的實(shí)現(xiàn)
2.1 編碼
    如果是一幅N×M的圖像，模板的大小為K×K,，那么可以將模板中心像素點(diǎn)在匹配圖中的坐標(biāo)位置(i,j)作為編碼的原始數(shù)據(jù),，可以采取22 bit二進(jìn)制編碼，把解空間的數(shù)據(jù)表示成一個(gè)個(gè)的二進(jìn)制串,。由于像素點(diǎn)在內(nèi)存中的存儲(chǔ)位置是從左到右從下到上,，本文把N×M圖像的最左下角點(diǎn)編碼為二進(jìn)制22 bit全0，最右上角點(diǎn)編碼為二進(jìn)制22 bit全1,。
2.2 初始化群體
    隨機(jī)產(chǎn)生N個(gè)初始化串結(jié)構(gòu)數(shù)據(jù),，每個(gè)串結(jié)構(gòu)數(shù)據(jù)稱為一個(gè)個(gè)體，組成最原始的群體,，以便后面迭代使用,。本文采取30個(gè)初始個(gè)體，進(jìn)化代數(shù)為100代,。

2.4 選擇
    采用經(jīng)典的輪盤賭的選擇方法,，每個(gè)個(gè)體進(jìn)入下一代的概率等于它的適應(yīng)度值和整個(gè)群體中每個(gè)個(gè)體適應(yīng)度值和的比例。也就是說適應(yīng)度越高,，被選中的可能性越大,，進(jìn)入下一代的可能性就越大[1]。
2.5 PC和Pm的調(diào)整
    如式(1)和式(2)所示,，分別設(shè)置k1,、k2、k3,、k4為0.3,、0.25、0.02,、0.01,。
2.6 交叉
    交叉是指對群體中隨機(jī)兩兩配對的個(gè)體進(jìn)行部分基因交換的過程，本文采用單點(diǎn)交叉的方式,，對交叉?zhèn)€體交叉點(diǎn)后面的二進(jìn)制位進(jìn)行互換,。例如：兩個(gè)個(gè)體的基因二進(jìn)制碼分別為0000101011100000100011和0000001111000001001100，交叉點(diǎn)位置為5,，交叉之后就會(huì)變成0000101111100000001100和0000001011100001100
011[5],。
2.7 變異
    變異是以較小的概率對個(gè)體編碼串中的某些位進(jìn)行變換，具體到二進(jìn)制編碼中就是將“1”變成“0”或是將“0”變成“1”。變異的概率由Pm決定,，不宜取太高,。
2.8 解碼
     當(dāng)滿足迭代次數(shù)之后，在最后一代的群體中選取適應(yīng)度最高的解即為最優(yōu)解,，將其二進(jìn)制碼進(jìn)行解碼之后就得到模板的位置了,。
3 固態(tài)流體測速的實(shí)現(xiàn)
    本文的最終目標(biāo)是為了測量圖2中礦料的流速。

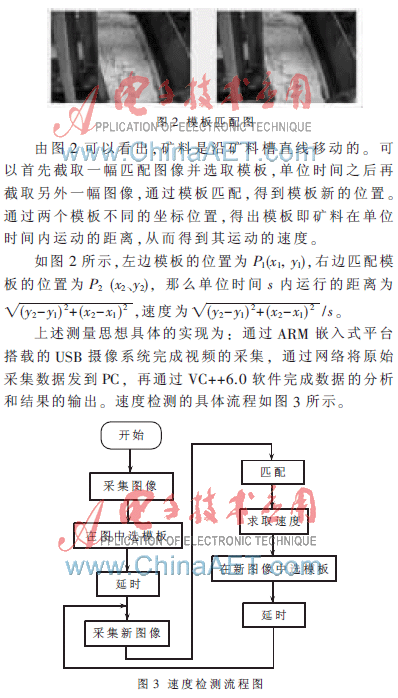
    從圖3可以看出,，這是一個(gè)連續(xù)匹配的過程,，其中有兩個(gè)問題必須注意：一是模板位置的選擇，顯然必須選接近礦料槽的中間位置,，這樣礦料比較穩(wěn)定,，不易向兩邊垮散；二是兩幅圖像間截取的時(shí)間延時(shí),，延時(shí)時(shí)間大小為兩幅圖像獲取時(shí)間的間隔減去之間算法消耗的時(shí)間, 因此時(shí)間不宜過短,，過短算法完不成，但也不能太長,，太長匹配區(qū)域很有可能變形,。經(jīng)過多次實(shí)驗(yàn)，在算法中選擇的匹配區(qū)域?yàn)?150,，90),、(180，90),、(150,，120)和(180，120)4個(gè)點(diǎn)組成的四邊形, 原始圖像大小為320×240,，延長時(shí)間為0.06 s,。
4 試驗(yàn)結(jié)果
    本文在VC++6.0軟件環(huán)境下進(jìn)行試驗(yàn)，首先對普通全局搜索模板進(jìn)行匹配,、簡單遺傳算法模板匹配以及自適應(yīng)遺傳算法模板匹配進(jìn)行了比較,對同一匹配點(diǎn)使用三種方法分別試驗(yàn)50次,，結(jié)果如表1所示。

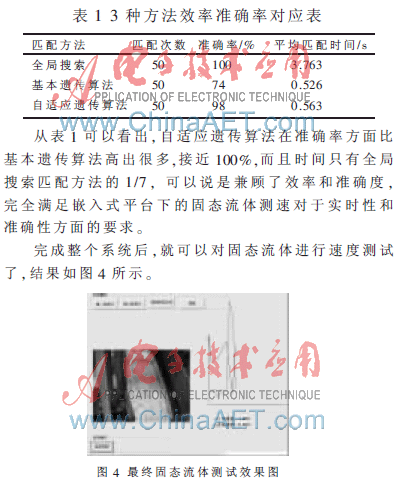
    本文以自適應(yīng)遺傳算法的模板匹配為理論基礎(chǔ),，提出了一種對固態(tài)流體的測速方法,。該方法高效準(zhǔn)確，能夠滿足實(shí)際需要,。當(dāng)然,，本文提出的方法還有很多方面的不足，比如自適應(yīng)遺傳算法的改進(jìn),，以及具體實(shí)施過程中的防抖,、光線等問題,，有待進(jìn)一步改進(jìn)。
參考文獻(xiàn)
[1] 王小平,，曹立明．遺傳算法——理論應(yīng)用于軟件實(shí)現(xiàn)[M]．西安：西安交通大學(xué)出版社,，2002．
[2] 英杰，張善文． Matlab遺傳算法工具箱及應(yīng)用[M]．西安：西安電子科技大學(xué)出版社,，2005．
[3] 鄭軍,，諸靜．基于自適應(yīng)的遺傳算法的圖像匹配[J]．浙江大學(xué)學(xué)報(bào),，2003,，37(6)：689-692．
[4] 巨永鋒， 藺廣逢,， 蔡占華． 基于遺傳算法的圖像識(shí)別技術(shù)[J]．長安大學(xué)學(xué)報(bào)(自然科學(xué)版),，2004，24(6)：98-101．
[5] MALLEY M E． A methodology for simulating the joint strike fighter’s prognostics and health management symem[D]．PhD．Department of the Air Force Air University,，2001．