摘 要:? 提出了一種改進(jìn)的交互式圖像分割算法,。采用全變分去噪模型對圖像進(jìn)行預(yù)處理,，在去除噪聲的同時(shí)更好地保護(hù)了邊緣；提出了一種對梯度模值進(jìn)行曲率加權(quán)的邊緣檢測方法,，采用該方法獲得圖像的邊緣點(diǎn)集,；將邊緣點(diǎn)集中曲率較大的邊緣點(diǎn)作為候選邊界點(diǎn)推薦給用戶；用戶通過主觀判斷,，在候選邊界點(diǎn)中選擇合適的“初始邊界點(diǎn)”,，算法便可采用GAC模型完成對目標(biāo)的分割。實(shí)驗(yàn)結(jié)果表明,，改進(jìn)算法提高了交互式圖像分割的自動(dòng)化程度,，有效地減少了交互過程中的人工參與量。
　　關(guān)鍵詞:? 圖像分割; 交互式;? TV_L1模型; 曲率加權(quán)梯度模值

?

　　在對圖像的研究和應(yīng)用中,，人們往往只對圖像的某個(gè)部分感興趣,，這些部分稱之為目標(biāo)或者對象，而其余部分稱為背景,。為了將目標(biāo)從背景中提取出來就需要采用圖像分割技術(shù),。圖像分割既可直接應(yīng)用于諸如醫(yī)療輔助診斷,、圖像修復(fù)、拼接等方面,，也可為后續(xù)的圖像分析和解釋,、基于對象的圖像(視頻)編碼等應(yīng)用提供基礎(chǔ)數(shù)據(jù)。
　　廣義上講,，圖像分割可分為兩大類：自動(dòng)分割和交互式分割,。傳統(tǒng)的自動(dòng)分割方法有基于灰度信息的投影分割法、直方圖分割法,、基于細(xì)節(jié)特征的邊緣檢測法等,。目前的基于偏微分方程的自動(dòng)分割方法在圖像處理領(lǐng)域得到迅速發(fā)展，其中最具代表性的就是測地線活動(dòng)輪廓GAC(Geodesic Active Contour)模型^[1-3],。
　　由于圖像的類型和內(nèi)容多種多樣,，自動(dòng)分割方法對多目標(biāo)或背景復(fù)雜的圖像很難奏效。因此,，往往需要一定的人工干預(yù),。目前，交互式圖像分割方法在醫(yī)療及臨床等領(lǐng)域有著廣泛的應(yīng)用,。然而,，通過人工目測的方式進(jìn)行圖像分割，不僅存在工作量大,、效率低的問題,，而且準(zhǔn)確度和一致性也難以得到保證。在交互式圖像分割方法研究中,，如何提高自動(dòng)化程度,，盡量減少人工干與，一直是人們努力的方向,。
　　本文提出一種可為用戶自動(dòng)提供候選邊界點(diǎn)的交互式圖像分割方法,。如何自動(dòng)提供數(shù)量少而有效的候選邊界點(diǎn)是本文研究的重點(diǎn)。
1 基于GAC模型的交互式圖像分割算法
　　基于GAC模型的交互式圖像分割方法[4]要求用戶參與的工作是:在待處理的圖像上給定少數(shù)幾個(gè)邊界點(diǎn){P_i,，i=1，…,，N},，之后，算法將自動(dòng)計(jì)算N段曲線,，它使每兩點(diǎn)(P_i,，P_i+1)(默認(rèn)P_N+1=P₁)之間的加權(quán)弧長為:
　　
　　達(dá)到最小(即最短路徑)，從而形成1條封閉曲線作為對象的輪廓,。式中g(shù)為邊緣函數(shù),。
引入函數(shù)v=1/g,，則式(1)可改寫為:

　　式(3)也稱為(動(dòng)態(tài))Hamilton-Jacobi方程。對它進(jìn)行數(shù)值計(jì)算時(shí),，可采用迎風(fēng)方案(Upwind Scheme)離散化,、計(jì)算等到達(dá)時(shí)間曲線。
　　待到達(dá)時(shí)間曲線計(jì)算完成之后,，就可以從Pi+1出發(fā),，進(jìn)行反向跟蹤而獲得P_i與P_i+1之間的最短程線，從而得到圖像的邊緣,。更詳細(xì)的算法流程可見參考文獻(xiàn)^[1],。
　　在基于GAC模型的交互式圖像分割方法中，其初始邊界點(diǎn)的選取是影響分割結(jié)果的重要步驟,。而用戶憑借視覺和經(jīng)驗(yàn)選取初始邊界點(diǎn),，不僅不夠恰當(dāng)或位置不夠精確，而且是一件很費(fèi)神的事情,。下面提出一種由計(jì)算機(jī)向用戶推薦初始邊界點(diǎn)的方法,，從而提高交互式圖像分割的自動(dòng)化程度。
2 改進(jìn)算法
2.1 TV_L1濾波
　　計(jì)算機(jī)推薦的邊界點(diǎn)原則上應(yīng)該是圖像邊緣點(diǎn),。為了減少噪聲的影響,，首先需要對圖像進(jìn)行平滑。眾所周知,，高斯濾波在去除噪聲的同時(shí)將導(dǎo)致邊緣模糊化,。由于交互式GAC分割技術(shù)本來就是針對邊緣微弱模糊的圖像所提出的，所以高斯濾波更不宜采用,。因此,，這里采用在濾除噪聲的同時(shí)能較好地保留邊緣的TV_L1模型對圖像進(jìn)行濾波。
　　TV_L1模型^[6]最早由Alliney提出,，其出發(fā)點(diǎn)是最小化如下能量泛函：
　　
　　式中,前一項(xiàng)是輸出圖像u的全變分(Total Variation),后一項(xiàng)是輸出圖像相對于輸入圖像u₀誤差的L¹范數(shù),λ為Lagrange乘子,，用于平衡兩項(xiàng)對“能量E”的貢獻(xiàn)。Chan和Esedoglu^[6]對此模型進(jìn)行了更深入的理論研究,，揭示出它具有非常優(yōu)越的尺度空間特性,。
　　(4)式對應(yīng)Euler-Lagrange方程為:

2.2 改進(jìn)的邊緣檢測算法
　　一般地，邊緣檢測的依據(jù)是圖像的梯度模值,，已被廣泛應(yīng)用的Canny算法[8]就是依據(jù)圖像的梯度模值來檢測邊緣的,。然而，事實(shí)上,，人們關(guān)注的邊緣除了梯度模值足夠大之外,，還需要足夠光滑?；谶@一考慮,，本文引入曲率加權(quán)梯度模值：

　　可以滿足權(quán)函數(shù)的這一要求,。式中，常數(shù)β用以控制下降的速率,。由于曲率的倒數(shù)是平面曲線密切圓的半徑,，當(dāng)用數(shù)字圖像的空間采樣間隔作為長度單位時(shí)，1條光順的邊緣的曲率半徑應(yīng)大于1,，即曲率絕對值應(yīng)小于1,。故選取β=2。
　　與Canny邊緣檢測算法類似,，計(jì)算出曲率加權(quán)梯度模值后,，用低閾值T1可得“弱邊緣”E₁，用高閾值可得“強(qiáng)邊緣”E₂,，顯然E₁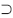E₂,。最終在E₁中僅保留與E₂有連通關(guān)系的連通分量作為輸出邊緣E。
2.3 候選點(diǎn)的獲取
　　原則上,，采用2.2節(jié)算法獲得的圖像邊緣點(diǎn)都可以作為初始邊界點(diǎn)的候選點(diǎn),，但是這種邊緣點(diǎn)的數(shù)量太多，不方便選擇,。為了減輕用戶選點(diǎn)的負(fù)擔(dān),，應(yīng)提供盡量少的候選點(diǎn)。由于曲率大的點(diǎn)往往是最受關(guān)心的初始邊界點(diǎn),，因此,，對已檢測出的邊緣點(diǎn)按曲率絕對值進(jìn)行降序排列，將大曲率的邊緣點(diǎn)優(yōu)先推薦給用戶,。這樣就可以大大減小用戶選點(diǎn)的難度,。對于只有1個(gè)對象的圖像分割，可以自動(dòng)選取前幾個(gè)點(diǎn)直接作為初始邊界點(diǎn),。而對于多個(gè)對象的分割,，可以通過多次人工指定包含被分割對象在內(nèi)的矩形區(qū)域，轉(zhuǎn)化為多次對單個(gè)對象的分割,，并最終完成全部對象的分割,。
　　綜上所述，改進(jìn)的基于GAC模型的交互式圖像分割算法可以描述如下：
　　(1)預(yù)處理,。采用TV_L1模型對圖像進(jìn)行平滑(取λ=0.5),。
　　(2)用8鄰點(diǎn)差分格式計(jì)算梯度和圖像等照度線的曲率:

?

　　(3)按照式(6)和式（7）計(jì)算曲率加權(quán)梯度模值。
　　(4)用低閾值T₁得“弱邊緣”E₁,，用高閾值T₂得“強(qiáng)邊緣”E₂，保留E₁中與E₂有連通關(guān)系的連通分量作為輸出邊緣E,。
　　(5)將邊緣點(diǎn)集按曲率絕對值進(jìn)行降序排列輸出,。
　　(6)用戶選擇邊界候選點(diǎn)后,，采用GAC模型實(shí)現(xiàn)圖像分割。
3 實(shí)驗(yàn)結(jié)果分析
　　為了驗(yàn)證本文方法的有效性和實(shí)用性,利用MATLAB的圖形用戶界面開發(fā)環(huán)境GUIDE,開發(fā)了簡單的交互式圖像分割圖形用戶界面,，對本文提出的邊緣檢測算法和分割進(jìn)行實(shí)驗(yàn)研究,。
3.1 邊緣檢測比較實(shí)驗(yàn)
　　將2.2節(jié)的邊緣檢測算法與經(jīng)典的Canny算法進(jìn)行實(shí)驗(yàn)比較。圖1中,，本文算法λ取0.3,高閾值T₂取0.966,，低閾值T₁取0.4×T₂；Canny算法中,高閾值T₂取0.5,，低閾值T₁取0.4×T₂,。圖2中,本文算法所取參數(shù)同圖1；Canny算法中,，高閾值T₂取0.42,，低閾值T₁取0.4×T₂。

　　從圖1和圖2不難看出,，改進(jìn)的邊緣檢測算法的效果優(yōu)于Canny算法,，主要表現(xiàn)在檢測出的邊緣更為準(zhǔn)確，并且雜亂的,、虛假的邊緣更少一些,。
3.2 單個(gè)對象的圖像分割
??? 圖3是對醫(yī)學(xué)圖像進(jìn)行分割的實(shí)驗(yàn)結(jié)果。圖3(a)中高閾值T₂取0.966,，低閾值T₁取0.4×T₂,。通過改進(jìn)的邊緣檢測方法進(jìn)行邊緣檢測，計(jì)算機(jī)自動(dòng)提供了足夠多而且精確的病變邊界候選點(diǎn)集,，且大曲率的邊緣點(diǎn)被優(yōu)先推薦,，此處選取如圖3(a)所示的6個(gè)初始邊界點(diǎn)，計(jì)算機(jī)便可精確地畫出圖像輪廓,。而圖3(b)中由于未選上曲率最大的點(diǎn),，最后得到的圖像分割結(jié)果不夠理想。

??? 圖4是對線粒體細(xì)胞圖像進(jìn)行的分割實(shí)驗(yàn),。實(shí)驗(yàn)參數(shù)同圖3,。圖4(a)是選取曲率大的初始邊界點(diǎn)后所得分割結(jié)果，圖4(b)的4個(gè)點(diǎn)通過隨機(jī)選取,，從實(shí)驗(yàn)結(jié)果可見,，圖4(a)的分割結(jié)果更為準(zhǔn)確。

　　以上實(shí)驗(yàn)結(jié)果表明,，在獲得足夠平滑的邊緣點(diǎn)集后,，選擇其中曲率較大的點(diǎn)作為初始邊界點(diǎn)的思路是正確的。由此可見,，除了要考慮曲率足夠大以外,，也需要注意所選初始點(diǎn)的空間分布應(yīng)該盡可能大一些,，也就是說，不要集中在一個(gè)局部取點(diǎn),，所選點(diǎn)之間應(yīng)該有一定的幾何距離,。這可以通過簡單的刪選程序?qū)崿F(xiàn)。
3.3 對多個(gè)對象進(jìn)行圖像分割
　　圖5是單純皰疹病毒感染細(xì)胞的超薄切片圖像分割實(shí)驗(yàn),。其中,，高閾值T₂取0.85，低閾值T₁取0.4×T₂,。圖中,，待分割圖像中包含多個(gè)目標(biāo)圖像，而實(shí)驗(yàn)僅選取其中的3個(gè)不同病毒細(xì)胞進(jìn)行圖像分割,。采取改進(jìn)的算法和本文開發(fā)的用戶圖形界面,，通過3次分別指定包含被分割病毒細(xì)胞在內(nèi)的矩形區(qū)域，逐次進(jìn)行單個(gè)目標(biāo)的分割,，最終實(shí)現(xiàn)了對3個(gè)病變細(xì)胞的準(zhǔn)確分割,。

?

　　針對交互式圖像分割方法的重要問題——如何更精確地選取“初始邊界點(diǎn)”并減輕交互過程中的人工量，本文提出了計(jì)算機(jī)自動(dòng)推薦候選邊界點(diǎn)的算法,，同時(shí)提出了對梯度模值進(jìn)行曲率加權(quán)的邊緣檢測方法,。為了驗(yàn)證本文算法的有效性，還開發(fā)了簡單的圖形用戶界面進(jìn)行實(shí)驗(yàn)研究,。通過開發(fā)的用戶圖形界面,，用戶只需在所列候選邊界點(diǎn)中選取“感興趣目標(biāo)”處的少數(shù)幾個(gè)點(diǎn)，便可得到圖像分割結(jié)果,。實(shí)驗(yàn)結(jié)果表明,，本文算法有效地提高了交互式圖像分割的自動(dòng)化程度，減少了交互過程中的人工參與量,，同時(shí)改善了由于人的主觀判斷所帶來的邊界點(diǎn)選取不精確的問題,。

參考文獻(xiàn)
[1] ?王大凱，侯榆青,，彭進(jìn)業(yè). 圖像處理的偏微分方程方法[M]. 北京：科學(xué)出版社,，2008.
[2] ?GONZALEZ R C, WOODS R W. 數(shù)字圖像處理.第二版[M]. 北京：電子工業(yè)出版社，2003:460-500.
[3] ?SAPIRO G. Geometric partial differential equations and?image processing. London: Cambridge University Press,2001.
[4] ?COHEN L D, KIMMEL R. Global minimum for active?contours models:A Minimal Path approach[J]. International ?Journal of Computer Vision,1997.
[5] ?ALLINEY S. Digital filters as absolute norm regularizers[J]. IEEE Transactions on Signal Processing, 1992,40(6):1548-1562 .
[6] ?CHAN T F, ESEDOGLU S. Aspects of total variation regularized L1 function approximation[J]. SIAM Journal on?Applied Mathematics, 2005, 65(5):1817-1837.
[7] ?VOGEL C R, OMAN M E. Fast robust total variation-based reconstruction of noisy, blurred images. IEEE, IP,?1998,7:813-824.
[8] ?CANNY J. A? computational approach to edge detection[J]. IEEE Transactions on PAMI, 1986,8(6):679-698.