IIR濾波器不易做成線性相位,，F(xiàn)IR濾波器只要滿足一定條件就可做成線性相位,，F(xiàn)IR濾波器有傳統(tǒng)的設(shè)計方法，如窗函數(shù)法,、頻率采樣法,、切比雪夫逼近法等;曾喆昭等人提出了一種基于余弦基神經(jīng)網(wǎng)絡(luò)的算法，給出了該算法的收斂條件,，并將其應(yīng)用到高階多通帶FIR濾波器中,，用實例說明了該算法在精度、計算速度等方面的優(yōu)越性,?；谶@種算法，有人分別將其在數(shù)域和維數(shù)上做出了推廣,。
本文提出的方法,，是基于余弦基神經(jīng)網(wǎng)絡(luò)設(shè)計方法的一種改良，其基本思想首先是使設(shè)計頻響與理想頻響之間的全局誤差在通帶和阻帶范圍最小,，其次再使用模擬退火算法,，以最小阻帶衰減為評價函數(shù)優(yōu)化網(wǎng)絡(luò)權(quán)值，使最后的結(jié)果朝著最優(yōu)值靠近。由該方法設(shè)計的濾波器,，通帶和阻帶范圍無過沖,、無波動，且阻帶的衰減高,，初始條件隨機給定,，算法速度快，因而是一種有效的設(shè)計方法,。
1 I型線性相位FIR濾波器的幅頻特性
若脈沖響應(yīng)h(n)是實序列,，且滿足h(n)=h(N-1-n)，N為脈沖響應(yīng)h(n)的長度,，并且N為奇數(shù),，則有：
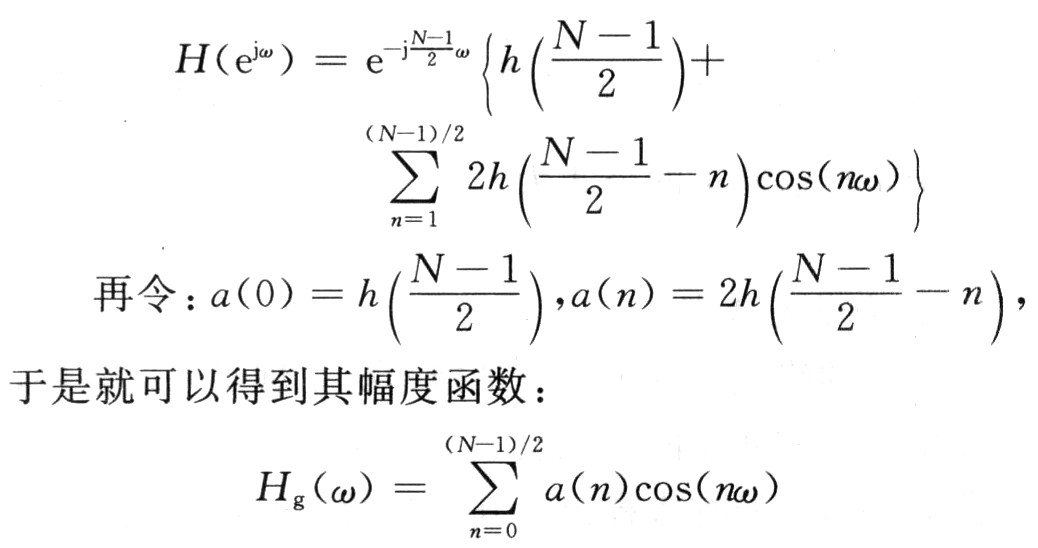
容易看出，此式是由(N+1)/2個余弦項迭加而成的函數(shù),，而此函數(shù)在ω=0,，π，2π處均不等于零,，因此I型線性相位FIR濾波器既可以用作低通濾波器(在ω=0處,，幅度函數(shù)不為零)，也可用作高通濾波器(在ω=π處,，幅度函數(shù)不為零),，而且也可以用作帶通和帶阻濾波器，是應(yīng)用最為廣泛的,。
2 余弦基神經(jīng)網(wǎng)絡(luò)
在網(wǎng)絡(luò)結(jié)構(gòu)方面,，如圖1所示，類似于BP網(wǎng)絡(luò)的結(jié)構(gòu)：
輸入層和輸出層都只有一個節(jié)點,，隱含層有M個節(jié)點，且各節(jié)點對應(yīng)的激勵函數(shù)如下：
式中：M=(N-1)/2
再令輸入層到隱含層的全值都為1,，而隱含層到輸出層的權(quán)值ω0～ωM分別取為a0～aM,，于是神經(jīng)網(wǎng)絡(luò)的輸入/輸出關(guān)系就恰好為濾波器的幅度函數(shù)
網(wǎng)絡(luò)學(xué)習(xí)算法方面，也可以采用類似BP網(wǎng)絡(luò)的學(xué)習(xí)算法,。
首先定義權(quán)值矩陣：
設(shè)置性能指標：
為訓(xùn)練樣本數(shù),。
于是權(quán)值修正的公式為：
式中：α為學(xué)習(xí)速率。
迭代的終止條件可設(shè)為性能指標J滿足一定條件,，而關(guān)于學(xué)習(xí)速率α的選取會直接影響到神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性,。目前，已經(jīng)有人提出了其適當?shù)倪x取范圍,，例如羅玉雄等人已經(jīng)證明,，當滿足0<α<(2/|| C ||2)時(這里||·||2表示的是歐氏范數(shù)的平方)，神經(jīng)網(wǎng)絡(luò)是穩(wěn)定的;曾喆昭等人也提出并證明了當滿足0<α<(4/N)時，神經(jīng)網(wǎng)絡(luò)是穩(wěn)定的,。
3 模擬退火算法
由于以上的網(wǎng)絡(luò)學(xué)習(xí)算法從本質(zhì)上來說,，還是一種BP算法，所以不可避免地會存在BP算法的缺陷,，初始值的選取會影響最終結(jié)果,，且容易陷入局部極小值。
模擬退火算法與初始值無關(guān),，算法求得的解與初始解狀態(tài)(是算法迭代的起點)無關(guān);模擬退火算法具有漸近收斂性,，在理論上已得到嚴格證明，當初溫充分高,，降溫足夠慢,，每一溫度下抽樣足夠長，最終溫度趨于零時,，算法最終以概率1收斂到全局最優(yōu)解,。模擬退火算法通過概率判斷來接受新狀態(tài)是算法在局部極小解處有機會跳出并最終趨于全局最優(yōu)的根本原因。于是將模擬退火算法加到前面的算法中去,，就可以很好地彌補上述算法的不足,。
模擬退火算法的步驟如下：
(1)由一個產(chǎn)生函數(shù)從當前解S產(chǎn)生一個位于解空間的新解S’。
(2)計算與新解所對應(yīng)的目標函數(shù)差,。這里以最小阻帶衰減為評價函數(shù)C(S),，這個函數(shù)可以由所得解S輕易地求出，于是目標函數(shù)差△t=C(S’)-C(S);
(3)判斷新解是否被接受,，其依據(jù)是一個接受準則,，最常用的接受準則是Metropolis準則。若△t≥0,，則接受S’作為新的當前解S;否則,，以概率exp(-△t/T)接受S’作為新的當前解S。
(4)當新解被確定接受時,，用新解代替當前解,，同時修正評價函數(shù)。此時,，當前解實現(xiàn)了一次迭代,，可在此基礎(chǔ)上開始下一輪試驗;當新解被判定為舍棄時，則在原當前解的基礎(chǔ)上繼續(xù)下一輪試驗,。
將模擬退火融入原算法,，其實主要是用原算法來實現(xiàn)模擬退火中第(1)步的產(chǎn)生解S，于是可得到總的算法：
(1)初始化,，初始溫度T(充分大),，初始解狀態(tài)S(是算法迭代的起點),，每個T值的迭代次數(shù)L，初始權(quán)值W,，性能指標J,，學(xué)習(xí)速率α，并且設(shè)定目標向量(理想幅頻響應(yīng)Hg(ωk));
(2)對k=1,，2,，…，L做第(3)～(8)步驟;
(3)計算誤差E(k),，使用權(quán)值修正公式：W=W+αE(k)C(Ωk)修正權(quán)值;
(4)滿足性能指標J轉(zhuǎn)步驟(5),，否則轉(zhuǎn)步驟(3);
(5)由步驟(4)產(chǎn)生的W得出新解S’;
(6)以濾波器的最小阻帶衰減為評價函數(shù)，計算△t,，其中△t=C(S)-C(S);
(7)若△t>0,，則接受S’作為新的當前解，否則以概率exp(-△t/T)接受S’作為新的當前解;
(8)如果滿足終止條件,，則輸出當前解作為最優(yōu)解,，終止條件通常取為連續(xù)若干個新解都沒有被接受;
(9)減小T，轉(zhuǎn)步驟(2),。當T→0時,，終止算法。
4 仿真實例
例1：設(shè)計一線性相位高通FIR濾波器,，其理想幅頻特性為：
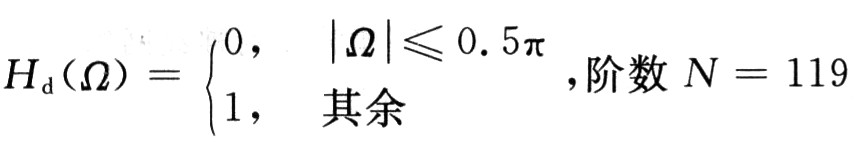
對Ω在[0,，π]范圍內(nèi)均勻取樣，共取(N+1)/2=60個樣點,，即Ωk=πk/59(k=0,，1，2,，…,，59)，為了使通帶和阻帶內(nèi)無過沖,、無波動,，在過渡帶內(nèi)取兩個點0.78和0.25，于是實際的幅頻取樣點為Hd(k)=[zeros(1,，29)，0.25,，0.78,，ones(1，29)];網(wǎng)絡(luò)結(jié)構(gòu)取為1×60×1,，性能指標設(shè)置為J=10-8,。
經(jīng)過計算機仿真得到如圖2和圖3的仿真圖,。
例2：設(shè)計一線性相位帶阻FIR濾波器，其理想幅頻特性為：
與例1類似,，對Ω在[0,，π]范圍內(nèi)均勻取樣，共取(N+1)/2=60個樣點,，即Ωk=πk/59,，(k=0，1,，2,，…，59),，同樣地,，為了使通帶和阻帶內(nèi)無過沖，無波動,，在過渡帶內(nèi)取兩個點0.78和0.25,，于是實際的幅頻取樣點為Hd(k)=[ones(1，17),，0.78,，0.25，zeros(1,，16),，0.25，0.78,，ones(1,，23)];網(wǎng)絡(luò)結(jié)構(gòu)取為1×60×1，性能指標設(shè)置為J=10-8,。
經(jīng)過計算機仿真得到如圖4和圖5的仿真圖,。
通過仿真，可以和與文獻[2]中的算法相比較,。在這里以例1中的情形為例,，兩種方法各運行10次，取最后得到的最小阻帶衰減(單位：dB)和程序的運行時間(單位：s)來比較：
文獻[2]中的算法：
兩者相比較可得,，雖然在運行時間上本文的算法遜于文獻[2]中的算法,，但這個運行時間本身也僅0.5 s左右，是可以接受的,。在性能上本文的算法得出的結(jié)果幾乎都在-190 dB左右,，而文獻E23中算法得出的結(jié)果則在-77～-93 dB之間波動，因此可以說用本文的算法可以得到更好,、更穩(wěn)定的最小阻帶衰減,。
5 結(jié) 語
本文方法的特點是先用類似BP網(wǎng)絡(luò)的方法調(diào)整神經(jīng)網(wǎng)絡(luò)權(quán)值,，再用模擬退火技術(shù)進行優(yōu)化，獲取更好的FIR濾波器的脈沖響應(yīng),，從而完成濾波器的設(shè)計,。由文中給出的兩個范例可以看出，設(shè)計濾波器的幅頻響應(yīng)在通帶與阻帶范圍均無過沖現(xiàn)象,，衰耗特性好,，阻帶最小衰減在190 dB以上，通帶沒有衰減,。而且這種方法可以輕松地實現(xiàn)低通,、高通、帶通,、帶阻FIR濾波器的設(shè)計,，程序運行時間均在0.5 s左右，是一種十分有效的設(shè)計方法,。