—個實際數(shù)字系統(tǒng)往往要求能夠工作在多采樣率狀態(tài),。多采樣率轉換是指對—個已知采樣頻率的信號進行重新抽樣,，使之變?yōu)橐粋€新采樣頻率的信號，若新采樣頻率比原來的小,，將此頻率轉換的過程稱作抽取,，否則，稱之為內(nèi)插,。多采樣率轉換是正交頻分復用(OFDM)的一項關鍵技術,，在很多數(shù)字信號處理教科書中都有介紹，但對多速率轉換引起的頻譜變化分析研究不夠透徹,。文中在已有工作的基礎上利用傅里葉變換的定義推導了抽取和插值后信號的頻譜變化,。

1 信號整數(shù)倍抽取
    已知連續(xù)信號為x(t)，以采樣率F1=1／T1(T1為采樣的間隔)進行等間隔采樣得到x(n),，M倍抽取后得到信號為y(n),，則抽取后序列對應的采樣率F2=1／T2,，其中，T2=MT1,，則有


    從式(5)可以看出,，整數(shù)倍抽取序列的數(shù)字譜是原序列x(n)的頻譜沿頻率軸擴展M倍且平移間隔為2π／M的M個平移樣本的迭加譜。
    如果輸入信號的頻譜>π／M,，將會混疊,，會給抽取信號的頻譜帶來失真，因為抽取信號的采樣速率不允許降到奈奎斯特采樣速率以下,，因此在抽取前應進行“反混淆”濾波,，該低通濾波器的截止頻率為π／M。

    令“反混疊”低通濾波器為理想濾波器
   

2 信號整數(shù)倍插值

    由式(9)可知,，插值后信號頻譜是原信號頻譜的L：1壓縮,。在實際的插值過程中，“插零”后還要經(jīng)過低通濾波,，濾波的目的在于消除填零過程引起的“復制”,。濾波采用理想的低通濾波器，其頻響為
   
    插值信號的頻譜為原信號沿頻率周壓縮L：1,。

3 計算機仿真
    信號x(t)=cos(2πf1t)+cos(2πf2t),，f1=15 Hz，f2=20 Hz,，以采樣頻率fs=100 Hz,，等間隔采樣N=256點，得到信號x(n),。為驗證抽取和插值對頻譜的影響,，做如下仿真。

    對x(n)進行M=2倍抽取,，得y(n)=x(2n),。

    對x(n)進行M=2倍抽取，得z(n)=x(4n),。

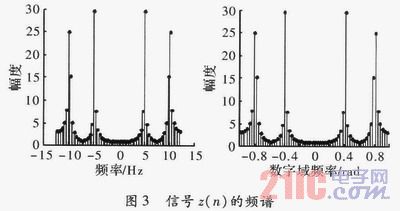
    從圖1～圖3可以看出,，M=2倍抽取采樣頻率為50 Hz滿足采樣頻率，抽取后頻率估計正確,，M=4倍抽取采樣頻率為25 Hz,，不滿足采樣定理，存在頻譜混疊現(xiàn)象,，頻率估計出錯,。對比圖1和圖2可以看出,，M=2倍抽取后,，數(shù)字域頻率展寬為原來的2倍,。
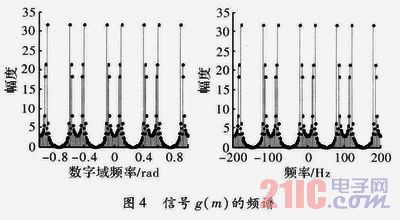
    對x(n)進行L=4倍零值內(nèi)插，得信號,。

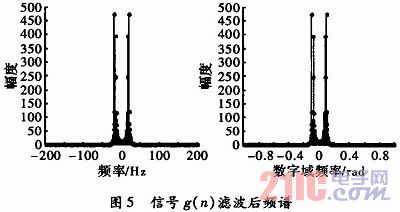
    其經(jīng)過的理想濾波器濾波后的頻譜如圖5所示,。

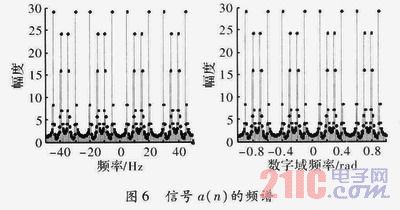
    對z(n)進行L=4零值內(nèi)插，得,。
    從圖4和圖5看出,，信號4倍零值內(nèi)插后的頻譜出現(xiàn)3個高頻鏡像譜，經(jīng)低通濾波后數(shù)字域頻譜壓縮為原來的1／4,。從圖6看出,，對不滿足采樣定理的信號z(n)進行4倍零值內(nèi)插后，仍然存在頻譜混疊,。

4 結束語
    在整數(shù)倍抽取時,，信號必須要滿足頻率采樣定理，才能使抽取后信號不發(fā)生頻譜混疊現(xiàn)象,，所得序列頻譜為原序列頻譜橫軸M倍擴展,。零值內(nèi)插序列的頻譜是原序列頻譜延拓L倍，讓其頻譜信號通過一個低通濾波器,，就可以得到有用的頻率分量,，其頻譜橫軸壓縮為原來的1／L。