1 頻率細化過程介紹
　　頻率細化是在信號處理和模態(tài)分析中廣泛應用的一種技術(shù),，它能夠提高頻率的分辨率,，將選定的頻率域上的特性曲線放大,，從而使系統(tǒng)的頻率特性能更清楚地顯示出來，如圖1所示,。

　　設(shè)系統(tǒng)的采樣頻率為fs,，采樣點數(shù)為NO，則頻率分辨率為：
　　Δf＝fs/NO
　　從上式可以看出,，要進行頻率細化,，即提高頻率分辨率，使Δf變小,，有兩種方法：增加采樣點數(shù)NO和降低采樣頻率fs,，這里只介紹降低采樣頻率的方法。
　　這種方法主要是基于移頻原理,，如圖2所示,。

　　設(shè)想要移頻部分的頻率為fp，其角頻率為ωp＝2πfp,，令f(t)＝exp(－jωpt)。時域信號x(t)與f(t)卷積后,，則在頻域上,，該信號的fp頻率就移到了原點處。
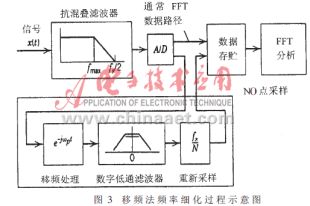
　　信號頻率移到低頻后,，經(jīng)過低通濾波,，就可以用低的采樣頻率進行采樣，從而達到提高頻率分辨率,、頻率細化的目的,。具體過程如圖3所示。
2 移頻法頻率細化過程中幾個問題的分析
　　(1)非細化處理的系統(tǒng)采樣頻率為fs,，采樣點數(shù)為NO,。對于細化過程，設(shè)頻率細化倍數(shù)為Nr,，信號經(jīng)過抗混疊濾波器后進行A/D采樣,，采樣頻率應仍為原來的fs，保持不變,，采樣點數(shù)則為Nr*NO,，這樣就保證了細化與非細化處理的基本頻帶范圍保持不變，并且可以細化這一頻帶中的任何一段,。
　　(2)要細化的頻率范圍為f1～fu,，移頻后，低頻點f1移到原點,，則高頻點變?yōu)?fu－f1),。這時數(shù)字低通濾波器的截止頻率應大于(fu－f1),，并小于低頻重采樣頻率fs/Nr的一半。即截止頻率的范圍為：
　　(fu－f1)＜fc＜fs/2Nr
　　且可以得到最大細化倍數(shù)N與細化頻率范圍之間的關(guān)系為：
　　Nr＜fs/2(fu－f1)
　　這為設(shè)置細化倍數(shù)范圍提供了依據(jù),。
　　(3)數(shù)字低通濾波器的通帶必須平,，通帶內(nèi)波動要小，這樣原信號的頻率特性細化后在幅值上才不會改變,；同時,，最好使濾波器的帶外衰減＞－70dB，且－70dB處的頻率＜fs/2Nr,，這樣就能保證低頻重新采樣時抗混疊的效果最好,，細化的效果也最好。
　　(4)細化與不細化過程占用時間的比較：由于采樣點數(shù)NO保持不變,，因此細化處理的FFT時間與不細化的FFT時間一樣,，都是NOlog(NO)/2；細化過程要進行Nr*NO點的高頻采樣和NO點的低頻采樣,，而不細化過程只進行NO點的高頻采樣,，所以在采樣時間上，細化過程要稍長一點,。但它與NO點的FFT變換時間比起來可以不計,，因此，細化處理與不細化處理在時間上差不多,。
　　(5)移頻法頻率細化與增加采樣點數(shù)頻率細化的比較：移頻法頻率細化只進行NO個點的FFT變換,，和一些數(shù)組、矩陣的運算,，它所花的時間約為：NOlog(NO)/2,；而采用增加采樣點數(shù)頻率細化要進行Nr*NO個點的FFT變換，它所花的時間約為：(Nr*NO)log(Nr*NO)/2,，因此采用移頻法頻率細化的時間要短得多,，這是它的優(yōu)點，也是工程應用中多采用這種方法的原因,，我們也只對它進行仿真,。
　　由于移頻使f1前面的頻段移到頻域的負軸上，而低通濾波又濾掉了fu后面的高頻部分,，因此,，這種方法只能進行一段頻率的細化，不能進行全頻段的細化,，這是移頻法頻率細化的缺點,。要進行全頻段細化，可以采用增加采樣點數(shù)的方法,。

3 用MATLAB仿真頻率細化過程
　　用MATLAB程序仿真圖3這個過程,，主要實現(xiàn)A/D采樣,、移頻、低通濾波,、低頻重新采樣,、FFT變換等，同時注意上面幾個問題的分析,。
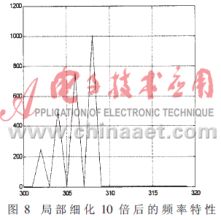
　　總信號由302Hz,、304Hz、306Hz,、308Hz四個不同頻率,、不同幅值的正余弦信號合成。采樣點為512,，采樣頻率為5120Hz,，則頻率分辨率為10Hz，這在頻域內(nèi)分辨不出這四個信號,。仿真軟件在300～320Hz范圍內(nèi)細化10倍,，則這時頻率分辨率為1Hz，就可以逐漸看清楚這四個信號,。
　　x(t)＝sin(2*302)+2cos(2π*304)+3sin(2π*306)+4sin(2π*308)
　　細化處理需要5120個采樣點,，仿真時A/D采樣用對連續(xù)信號x(t)進行離散化來代替，離散化的點值就是采樣值,，它們組成一個數(shù)組(矩陣)，這是一個點序列,。
　　采樣完成后,，對采樣點進行移頻仿真(將300Hz移頻到原點)，由以下步驟實現(xiàn)：
　　令：f1＝300,ω1＝2π*f1
　　f(t)＝exp(－jω1*t)
　　t取離散化時刻,，Δt＝1/fs,Tk＝k*Δt
　　則f(t)離散化可變?yōu)椋?BR>　　f(k)＝exp(－jω1*Tk)
　?。絜xp[(－j2π*f1*k)/fs]
　　這也是一個點序列。
　　MATLAB將上面兩個點序列進行卷積(矩陣相乘),，得到一個新的點序列,，就實現(xiàn)了移頻過程，即使f1＝300Hz 在頻域上移動了0,，其它頻率特性依此前移,。
　　MATLAB語言有很方便的濾波器設(shè)計和數(shù)字濾波功能，可用它設(shè)計一個帶內(nèi)波動＜0.1dB,，帶外衰減＞－70dB,，截止頻率為20Hz的低通濾波器，并將上面的點序列進行數(shù)字濾波,，得到一個只在0～20Hz頻段上有特性曲線,、其它頻段被濾掉的信號的點序列,。
　　對上面的點序列每隔10點(細化倍數(shù))進行抽取，實際上就是對經(jīng)移頻,、濾波后的信號進行重新采樣,。采樣頻率為5120Hz/10，即采樣頻率降低了10倍,，抽取得到512個點,。
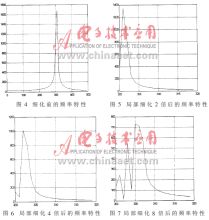
　　對這512個點進行FFT變換，就可以得到300Hz～320Hz頻段上已細化10倍的頻率特性曲線了,，結(jié)果如圖4,、圖8所示。

?