摘 要: 運用MATLAB編程實現(xiàn)遺傳算法,數(shù)值仿真驗證了該實現(xiàn)方法的有效性,,表明它能夠?qū)瘮?shù)進行全局尋優(yōu),。這種實現(xiàn)方法既可以熟悉MATLAB語言,又可以加深對遺傳算法的認識和理解,,以此來設(shè)計智能系統(tǒng)。
關(guān)鍵詞: MATLAB 遺傳算法 優(yōu)化
遺傳算法(Genetic Algoritms,,簡稱GA)是以自然選擇和遺傳理論為基礎(chǔ),,將生物進化過程中適者生存規(guī)則與群體內(nèi)部染色體的隨機信息交換機制相結(jié)合的搜索算法。自從1975年John H.Holland教授出版GA的經(jīng)典之作“Adaptation in Natural and Artificial Systems”以來,,GA已獲得廣泛應(yīng)用,。
1 遺傳算法簡介
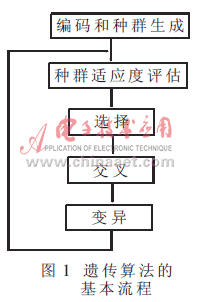
遺傳算法是具有“生成+檢測”的迭代過程的搜索算法?;玖鞒倘鐖D1所示,??梢姡z傳算法是一種群體型操作,,該操作以群體中的所有個體為對象,。選擇(selection)、交叉(crossover)和變異(mutation)是遺傳算法的三個主要操作算子,。遺傳算法包含如下6個基本要素:
(1)參數(shù)編碼:由于遺傳算法不能直接處理解空間的解數(shù)據(jù),,因此必須通過編碼將它們表示成遺傳空間的基因型串結(jié)構(gòu)數(shù)據(jù)。
(2)生成初始群體:由于遺傳算法的群體型操作需要,,所以必須為遺傳操作準備一個由若干初始解組成的初始群體,。初始群體的每個個體都是通過隨機方法產(chǎn)生的。
(3)適應(yīng)度評估檢測:遺傳算法在搜索進化過程中一般不需要其他外部信息,,僅用適應(yīng)度(fitness)值來評估個體或解的優(yōu)劣,,并作為以后遺傳操作的依據(jù)。
(4)選擇(selection):選擇或復(fù)制操作是為了從當(dāng)前群體中選出優(yōu)良的個體,,使它們有機會作為父代為下一代繁殖子孫,。個體適應(yīng)度越高,其被選擇的機會就越多,。本文采用與適應(yīng)度成比例的概率方法進行選擇,。具體地說,就是首先計算群體中所有個體適應(yīng)度的總和(∑f),,再計算每個個體的適應(yīng)度所占的比例(fi/∑f),,并以此作為相應(yīng)的選擇概率ps。
(5)交叉操作:交叉操作是遺傳算法中最主要的遺傳操作,。簡單的交叉(即一點交叉)可分兩步進行:首先對種群中個體進行隨機配對,;其次,在配對個體中隨機設(shè)定交叉處,,配對個體彼此交換部分信息,。
(6)變異:變異操作是按位(bit)進行的,即把某一位的內(nèi)容進行變異,。變異操作同樣也是隨機進行的,。一般而言,變異概率pm都取得較小,。變異操作是十分微妙的遺傳操作,,它需要和交叉操作配合使用,目的是挖掘群體中個體的多樣性,,克服有可能限于局部解的弊病。
2 基于MATLAB的遺傳算法的實現(xiàn)
為簡單起見,,我們假設(shè)尋求一單變量函數(shù)F(x)的全局最優(yōu)解,,x對應(yīng)于[a,b],,下面介紹實現(xiàn)步驟。
2.1 初始化
首先用二進制串表示初始種群中的個體,,每一個體由一系列二進制位(0和1)組成,,stringlength和popsize分別表示二進制序列的長度和初始種群的個體個數(shù),每一個體用如圖2的方式來編碼,,整個初始種群的數(shù)據(jù)結(jié)構(gòu)由大小為popsize*(stringlength+2)的矩陣實現(xiàn),。

第一列stringlength包括了初始真值x的二進制編碼,該串是隨機產(chǎn)生的,,但必須滿足在x的定義域[a,b]中,,交叉和變異操作將會對此串進行操作,第(stringlength+1)和(stringlength+2)列分別包含x真值和x的適應(yīng)度函數(shù)F(x),,于是用以下代碼實現(xiàn)初始化過程:
function[pop]=initialise(popsize,stringlength,fun);
pop=round(rand(popsize,stringlength+2));
pop(:,stringlength+1)=sum(2.^(size(pop(;,1:stringlength),2)-1:-1:0).
pop(:,1:stringlength)(b-a)/(2.^stringlength-1)+a;
pop(:,stringlength+2)=fun(pop(;,stringlrngth+1);
end
在上面代碼中,,首先隨機產(chǎn)生二進制串,然后用x的真值和目標函數(shù)填充到(stringlength+1)和(stringlength+2)中,,其中fun為目標函數(shù),,以.m的文件形式存在。
2.2 交叉
交叉過程選取兩個體作為父代parent1,parent2,,產(chǎn)生出兩新的子代個體child1和child2,,pc表示交叉概率,交叉算子的實現(xiàn)過程如下:
function[child1,child2]=crossover(parent1,parent2,pc);
if(rand<pc)
cpoint=round(rand*stringlength-2))+1;
child1=[parent(:,1:cpoint)parent2(:,cpoint1+1:stringlength)];
child2=[parent2(:,1:cpoint)parent1(:,cpoint1+1:stringlength)];
child1(:,stringlength+1)=sum(2.^(size(child1(:,1:stringlength),2)-1:-1:0).
*child1(:,1:stringlength))*(b-a)/(2.^stringlength-1)+a;
child2(:,stringlength+1)=sum(2.^(size(child2(:,1:stringlength),2)-1:-1:0).
*child2(:,1:stringlength))*(b-a)/(2.^stringlength-1)+a;
child1(:,stringlength+2)=fun(child1(:,stringlength+1));
child2(:,stringlength+2)=fun(child1(:,stringlength+1));
else
child1=parent1;
child2=parent2;
end
end
在交叉過程的開始,,先產(chǎn)生隨機數(shù)與交叉概率相比較,,如果隨機數(shù)比pc小,則進行交叉運算,,否則將不會進行交叉運算,,直接返回父代。一旦進行交叉運算,,交叉斷點cpoint將在1和stringlength之間選取,,交叉點cpoint是由隨機函數(shù)在1和(stringlength-1)之間返回一偽隨機整數(shù),于是獲得新的子代個體的真值和其適應(yīng)度,。
2.3 變異
變異操作由一個父代parent產(chǎn)生單個子代child,,pm表示變異概率,如果在目前父代允許變異的情況下,,我們選擇變異點mpoint使該位取反,,可同樣獲得新的子代的真值和適應(yīng)度。
function[child]=mutation(parent,pm);
if(rand<pm)
mpoint=round(rand*(stringlength-1))+1;
child=parent;
child[mpoint]=ads([parent[mpoint]-1);
child(:,stringlength+1)=sum(2.^(size(child(:,1:stringlength),2)-1:-1:0).
*child(:,1:stringlength))*(b-a)/(2.^stringlength-1)+a;
child=(:,stringlength+2)=fun(child(:,stringlength+1);
else
child=parent;
end
end
2.4 選擇
選擇或復(fù)制操作是決定哪些個體可以進入下一代,。程序中采用賭輪盤選擇法選擇,,這種方法較易實現(xiàn)。根據(jù)方程fi/∑f>0計算出每個個體被選擇的概率,向量prob包含了選擇概率之和,,向量rns包含歸一化過的隨機數(shù),,經(jīng)過比較rns和prob向量中的元素,我們可以選擇出進入下一代的個體,。
function[newpop]=roulette(oldpop);
totalfit=sum(oldpop(:,stringlength+2);
prob=oldpop(:,stringlength+2)/totalfit;
prob=cumsum(prob);
rns=sort(rand(popsize,1));
fitin=1;newin=1;
while newin<=popsize
if(rns(newin)<prob(fitin))
newpop(newin,:)=oldpop(fitin,:);
newin=newin+1;
else
fitin=fitin+1;
end
end
3 仿真例
為了驗證基于MATLAB設(shè)計的遺傳算法的全局尋優(yōu)能力,,舉例驗證??紤]一單變量函數(shù)為:
f(x)=x+10*sin(5x)+7*cos(4x)????????? (2)
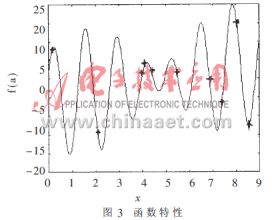
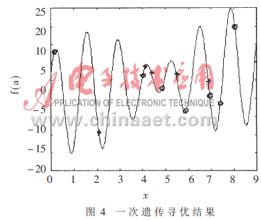
x∈[0,9],。按照上述方法,取popsize=10,stringlength=20,pc=0.95,pm=.08,。圖3為此函數(shù)的特性,,圖中‘+’表示隨機產(chǎn)生的10個函數(shù)值;圖4中‘o’為經(jīng)過一代遺傳,,得到的尋優(yōu)值,;經(jīng)過25代遺傳運算,得到函數(shù)的全局最大值,,如圖5中的‘*’:即當(dāng)x為7.8569時函數(shù)取得最大值24.8554,。
本文用MATLAB語言實現(xiàn)了遺傳算法的各項遺傳操作,如交叉,、變異和選擇等,,仿真例檢驗了該方法的有效性。采用這種方法既可以使大家熟悉MATLAB語言,,又可以加深對遺傳算法的認識和理解,,以此來設(shè)計智能系統(tǒng)。
參考文獻
1 D.E.Goldberg.Genetic algorithms in search,optimization and machine learning.Addison-Wesley,1989
2 孫增圻.智能控制理論與技術(shù).北京:清華大學(xué)出版社,,1997
3 席裕庚.遺傳算法綜述.控制理論及應(yīng)用,,1996,13(6):697-708
4 Y.J.Cao,Q.H.Wu.Teaching Genetic Algorithm Using MAT-LAB.Int.Journal Electrical Engineering on Education,1998(2):139-152