??? 摘? 要:?采用雙Booth 2編碼技術(shù),,對高基radix-16 Montgomery模乘法器進(jìn)行了優(yōu)化設(shè)計,,減小了電路面積,提高了模乘運算速度,。使用SMIC0.18μm標(biāo)準(zhǔn)單元工藝庫綜合后,,計算256bit有限域GF(p)上的模乘只需要0.51μs,。?
??? 關(guān)鍵詞: 布斯編碼; Montgomery,; 有限域,; 模乘法器
?
??? RSA算法、數(shù)字簽名標(biāo)準(zhǔn),、橢圓曲線密碼系統(tǒng)都要涉及到模乘或模冪運算,。Montgomery模乘算法[1]把模乘運算時的除法運算轉(zhuǎn)換成了簡單的移位操作,大大提高了模乘運算的速度,,從而得到了廣泛的應(yīng)用[2-4],。公鑰密碼體制中模乘運算的操作數(shù)位寬很大,ECC需要160~512bit,,RSA等甚至達(dá)到1 024~2 048bit,。直接利用原始的Montgomery模乘算法只能處理固定位寬的操作數(shù),,而且速度和面積均不理想。為此,一種基于字的Montgomery模乘算法被提了出來[2],,該算法不僅大大縮短了關(guān)鍵路徑,,而且可將操作數(shù)擴展到任意位寬。目前已有多種基于這種算法的模乘法器設(shè)計方案[3-4],。本文基于雙Booth 2編碼提出了另一種改進(jìn)方案并進(jìn)行了優(yōu)化設(shè)計,,使得模乘運算的速度得到了進(jìn)一步的提高。?
1 基于字的雙有限域Montgomery模乘算法?
??? Tenca[2]提出了基于字的雙有限域Montgomery模乘算法,?;谶@種算法設(shè)計的模乘法器采用基于字的操作數(shù)代替固定長度操作數(shù),不但解決了大數(shù)加法進(jìn)位鏈過長使電路關(guān)鍵路徑延遲太大的問題,,而且使得模乘法器具有了可擴展性,,能支持任意位長的模乘。把素數(shù)域GF(p)與二進(jìn)制域GF(2m)上的模乘統(tǒng)一起來則能在一個硬件上支持兩種域上的運算,,從而節(jié)省了成本,。基于字的雙有限域Montgomery模乘算法如下:?
??? Input: A,B,p,w,k,field?
??? Output: C∈[1,p-1]?
??? 1a: C=0?
??? 1b: spill=0?
??? 2: for i=0 to u-1?
??? 3: (spill|c0)=(aib0)φc0?
??? 4: q=f(c0,p0,field)?
??? 5a: (spill|c0)=(q·p0)φ(spill|c0)?
??? 5b: for j=0 to e-1?
??? 5c: (spill|cj)=(ai·bj)φcjφspillφ(q·pj)?
??? 6a: cj-1=(cj|cj-1)/r mod w?
??? 6b: ce-1=(spill|ce-1)/r mod w?
??? 6c: ce=0?
??? 7: if C>p, then C=C-p?
??? 算法把m bit模乘操作數(shù)擴展后看作基于字的向量,,然后對操作數(shù)逐字掃描進(jìn)行運算,。其中,p=(0,pe-1,…,p1,p0),B=0(0,be-1,…,b1,b0),C=(0,ce-1,…,c1,c0),A=(au-1,…,a1,a0),pi、bi,、ci是基為2w的字,,ai是基為2k的字,u= 二進(jìn)制域上多項式A(x)可以簡單地看成素數(shù)域上的A,只是在部分積累加時有區(qū)別,,素數(shù)域上有進(jìn)位的傳播,,二進(jìn)制域上為“異或”運算無進(jìn)位,算法中統(tǒng)一用φ表示,。函數(shù)f(c0,p0,field)只用到了c0,、p0的最低k bit,有限域GF(p)上q=(c0·(2k-p0-1))mod r,,有限域GF(2m)上q=(c0·p0-1)mod r,。?
二進(jìn)制域上多項式A(x)可以簡單地看成素數(shù)域上的A,只是在部分積累加時有區(qū)別,,素數(shù)域上有進(jìn)位的傳播,,二進(jìn)制域上為“異或”運算無進(jìn)位,算法中統(tǒng)一用φ表示,。函數(shù)f(c0,p0,field)只用到了c0,、p0的最低k bit,有限域GF(p)上q=(c0·(2k-p0-1))mod r,,有限域GF(2m)上q=(c0·p0-1)mod r,。?
??? Tenca[2]把上述Montgomery模乘算法組織成了流水線結(jié)構(gòu)。它包括s級處理單元(PE),,每個PE運算單元做兩次一個字長的加法,,加法器采用帶域選擇信號field的進(jìn)位保留加法器(CSA),運算結(jié)果經(jīng)過一級流水線寄存器后傳給下一級PE運算單元,。PE經(jīng)重定時優(yōu)化后采用兩級寄存器結(jié)構(gòu),,第一級計算q,第二級完成第5步的累加,。PE每次處理3bit的A,,即對A的編碼采用基為8的Booth 3編碼,。為面向RSA應(yīng)用,Yibo Fan[3]在素數(shù)域GF(p)上對Tenca[2]提出的結(jié)構(gòu)進(jìn)行了優(yōu)化,,采用基為16的Booth 4編碼,,提高了近26%的性能。?
2 雙Booth 2雙有限域模乘法器的設(shè)計?
??? Yibo Fan[3]采用的處理單元PE采用分裂基的方法簡化對ai的Booth編碼,,有效避免了不規(guī)則bi,、pi的倍數(shù)(如出現(xiàn)3bi、7pi),,但其需要六選一的數(shù)據(jù)選擇器,,而且左右兩個數(shù)據(jù)選擇器不一樣,造成布局布線的不規(guī)則,。本文經(jīng)研究發(fā)現(xiàn)可以把基為16的ai分成兩個基為4的操作數(shù)同時操作,,仍然可采用類似分裂基的硬件結(jié)構(gòu),而且左右數(shù)據(jù)選擇器相同,,使得VLSI實現(xiàn)時布線更容易,;對基為4的操作數(shù)采用Booth 2編碼后,編碼器結(jié)構(gòu)也更簡單,,數(shù)據(jù)選擇器的輸入只有0,、bi、-bi,、2bi、-2bi,,它們只需要經(jīng)過簡單的移位與取反操作就能夠?qū)崿F(xiàn),,從而減小了電路面積。編碼電路和數(shù)據(jù)選擇器電路更加簡單還可以縮短關(guān)鍵路徑的延遲,,從而提高了模乘法器的速度,。?
2.1 總體結(jié)構(gòu)設(shè)計與優(yōu)化?
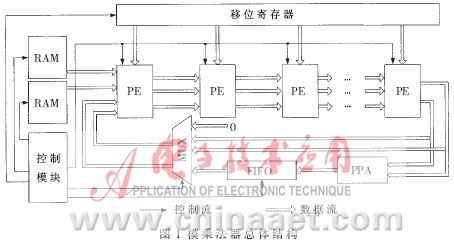
??? 雙Booth 2雙有限域模乘法器的核心仍然是基于字的Montgomery模乘算法,因此也可以組織成流水線結(jié)構(gòu),,如圖1所示,。它由s個處理單元(PE)、一個移位寄存器,、兩個同步讀寫RAM,、一個異步FIFO以及控制模塊組成。移位寄存器根據(jù)算法外層循環(huán)依次移位輸出ai,,兩個同步讀寫RAM則根據(jù)算法內(nèi)層循環(huán)輸出bi,、pi。如果在模乘運算中出現(xiàn)流水線溢出,,則把中間結(jié)果暫存到FIFO中,,等待流水線空閑,;如果不出現(xiàn)流水線溢出,則旁路掉FIFO直接使中間結(jié)果進(jìn)入新的流水線,。PE處理后的數(shù)據(jù)是以carry-save的冗余形式表示的,,中間數(shù)據(jù)位寬增大了一倍,造成FIFO需要增大一倍,。由于FIFO一路的中間結(jié)果不處在關(guān)鍵路徑上,,可以用一個并行前綴加法器PPA把carry-save冗余形式轉(zhuǎn)化為整數(shù)形式,這樣可以節(jié)省一半的FIFO,。Tenca[2]實現(xiàn)的模乘法器中使用循環(huán)寄存器存儲bi,、pi需要占用大量的面積,而本文使用RAM代替可以充分利用標(biāo)準(zhǔn)單元庫的資源,減小了電路面積,。?
?
?
2.2 模乘處理單元結(jié)構(gòu)?
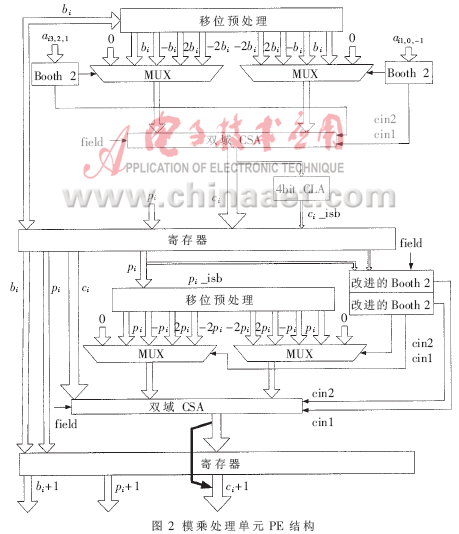
??? 模乘處理單元PE是模乘法器的核心部件,,若干級PE通過流水線寄存器串聯(lián)起來執(zhí)行大數(shù)模乘運算,其電路結(jié)構(gòu)如圖2所示,。它包含4個五選一的數(shù)據(jù)選擇器,、2個雙有限域進(jìn)位加法器CSA、1個4位超前進(jìn)位加法器CLA,、2個Booth 2編碼器,、2個修改的Booth 2編碼器及若干寄存器。為了提高電路工作頻率,,用寄存器把PE電路分成兩個部分,,使其用兩個時鐘完成部分積的累加。為平衡路徑延遲,,把兩個CSA放在寄存器的兩邊,。由于第二個時鐘周期內(nèi)的編碼電路比第一個時鐘周期內(nèi)的編碼電路要復(fù)雜,延時更大,,如果把4位CLA放在第一個時鐘內(nèi)計算則剛好能達(dá)到大致平衡,。?
?
?
??? 乘數(shù)A每次掃描4位,分成兩組,,每組2位,,經(jīng)Booth 2編碼后得到3位的輸入數(shù)據(jù)控制數(shù)據(jù)選擇器的輸出。函數(shù)f通過編碼器實現(xiàn),,有限域GF(p)與GF(2m)上的q值計算不一樣,,因此需要同時編碼并通過域選擇信號field選擇輸出。編碼輸出的四位q值再次經(jīng)過雙Booth 2編碼控制數(shù)據(jù)選擇器的輸出,。上述分兩步的編碼方式其中間值q是可以省略的,,直接修改Booth 2編碼的輸入信號,一次編碼完成,,部分編碼如表1所示,。?
?

?
3 實現(xiàn)結(jié)果?
??? 基于雙Booth 2編碼的雙有限域模乘法器作為核心部件應(yīng)用在雙有限域ECC協(xié)處理器中,,根據(jù)協(xié)處理器的實際需要,處理的最長操作數(shù)為384位,,因此模乘法器采用4級流水,;bi、pi的字寬為32位,,便于與常用總線連接,。這種設(shè)計既考慮了處理速度,又兼顧了電路占用的面積,。模乘法器用Verilog語言描述,,采用Synopsys公司的Design Complier 在SIMC 0.18μm-typcal工藝庫下綜合,等效“與非門”為4.5萬門,,最高工作頻率可達(dá)280MHz,,完成一次GF(p)上的256bit模乘運算只需要0.51μs。表2是本文設(shè)計的模乘法器與已發(fā)表文獻(xiàn)中同類設(shè)計的比較結(jié)果,。表中結(jié)果顯示,本文設(shè)計的速度比最好的已發(fā)表的設(shè)計[3]提高了16%,。?
?

?
??? 雙有限域模乘法器使用同一套硬件電路實現(xiàn)有限域GP(p)與GF(2m)上的ECC模乘運算,節(jié)約了硬件成本,,擴展了運用空間,。本文基于雙Booth 2編碼對基為16的Booth 4編碼的模乘法器進(jìn)行了優(yōu)化,使得電路更加規(guī)范,、簡單,。從實現(xiàn)結(jié)果可以看出,本文的設(shè)計有效地減小了關(guān)鍵路徑延遲,,提高了模乘法器的運算速度,。?
參考文獻(xiàn)?
[1] MONTGOMERY P L. Mondular multiplication without trial?division. Mathematics of Computation, 1985,44(7):519-521.?
[2] TENCA A F, SAVAS E, KOC C K. A design framework?for scalable and unified multipliers in GF(p) and GF(2m).?International Journal of Computer Research, 2004,13(1):68-83.?
[3] FAN Yi Bo, ZENG Xiao Yang, GANG Yi Yu,et al. A?modified high-radix scalable montgomery multiplier. IEEE??International Symposium on Circuit and System(ISCAS),?Island of ? Kos, Greece, May. 2006.?
[4] 史焱,吳行軍.高速雙有限域加密協(xié)處理器設(shè)計.微電子學(xué)與計算機,2005,22(5):8-12.

