摘  要： 提出在支持向量機回歸預測中采用粒子群算法優(yōu)化參數和主成分析降維的方法,，通過算例分析表明,，此法能夠顯著提高預測的精度。
關鍵詞： 支持向量機；粒子群算法,；主成分析法,；預測

    預測是國家、企業(yè)等組織制定政策和計劃的主要依據,，因而預測的準確度是政策與計劃制定是否科學的前提,。預測的方法有傳統的多元回歸預測，以及近幾年來發(fā)展起來的人工神經網絡預測[1],、灰色預測[2],。多元回歸預測模型簡單、易用性強,，但難以處理高維,、非線性模式；人工神經網絡雖然能夠較好地解決高維非線性預測的難題,，但它需要大量的訓練樣本,，且泛化能力不強，所以當可得到的預測樣本是小樣本,，或者獲得大量樣本的成本很高時,，就難免影響其實用性和經濟性；灰色預測雖具有短期預測能力強,，可檢驗等優(yōu)點,，但其長期預測能力較差。Vapnik等人提出的支持向量機[3-4]是在統計學習理論基礎上發(fā)展起來的一種新的機器學習算法,，是目前針對小樣本統計和預測學習的最佳理論,，支持向量機具有完美的數學形式、直觀的幾何解釋和良好的泛化性能,，解決了模型選擇與欠學習,、過學習及非線性等問題，克服了收斂速度慢,，易陷入局部最優(yōu)解等缺點,，因此支持向量機在分類和回歸中均表現出優(yōu)越的性能。

射函數,。核函數的作用是當樣本點在原空間線性不可分時,，可以通過映射函數映射到高維空間，從而達到線性可分的目的,，但實際應用中映射函數的顯式表達式很難找到,，觀察式(2)~式(4)中只用到了映射在高維空間的點積，而核函數的特點就是能使變量在低維空間核函數值等于其映射到高維空間的點積值,，從而實現不需要知道顯式映射函數達到向高維空間映射的目的,。任何滿足Mercer 條件的函數均可作為核函數,。
2 粒子群算法基本原理
    微粒群算法最早是在1995年由美國社會心理學家Kennedy和Russell[6]共同提出，其基本思想是受鳥群覓食行為的啟發(fā)而形成的,。PSO算法把優(yōu)化問題的解看作是D維空間中一個沒有體積沒有質量的飛行粒子，所有的粒子都有一個被優(yōu)化目標函數決定的適應度值,，而速度決定每個粒子的飛行方向和距離,，粒子根據自己先前達到的最優(yōu)位置和整個群體達到的最優(yōu)位置來更新自己的位置和速度，從而向全局最優(yōu)位置聚集,。粒子根據以下公式來更新自己的速度和位置：

4 應用實例
    試驗從UCI上選取美國波斯頓地區(qū)1993年城鎮(zhèn)住房數據作為試驗數據[9],。試驗步驟如下：
    (1)應用主成分析法降維
    由于統計軟件SPSS提供了主成份分析功能，而且具有采用交互式,、圖形化操作界面,、結果圖形化輸出、直觀性強等優(yōu)點,，故本文采用SPSS16.0作為降維工具,，表1為最大方差旋轉后的因子載荷圖，從表中可以看出,，7個主成份都有很好的解釋意義(載荷絕對值>0.5,，說明變量與主成份存在相關性)。主成份1為城鎮(zhèn)生活環(huán)境,，主成份2為治安環(huán)境,，主成份3為人口密度，主成份4為人口層次,，主成份5為是否有河流,，主成份6為商業(yè)環(huán)境，主成份7為教育發(fā)展水平,。

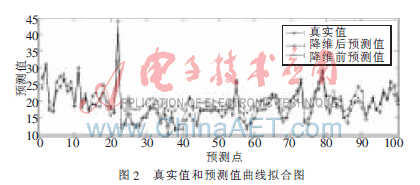
    本文把量子群優(yōu)化算法和主成分析降維的方法應用于支持向量機的回歸預測中,，試驗結果表明此法能顯著提高支持向量機的預測精度，同時也表明了支持向量機在非線性,、高維模式下的良好預測性能,。
參考文獻
[1] 閻平凡，張長水.人工神經網絡與模擬進化計算[M].北京：清華大學出版社,，2006.
[2] 韋康南,，姚立綱等.基于灰色理論的產品壽命預測研究[J].計算機集成制造系統，2005(10)：1491-1495.
[3] VAPNIK V N. The nature of statistic learning theory[M].New York： Springer,， 2005.
[4] VAPNIK V N. Estimation of dependencies based on empiric[M]. Berlin Springer-Verlag,， 2003.
[5] 鄧乃揚，田英杰. 數據挖掘中的新方法-支持向量機[M].北京：科學出版社,，2004.
[6] KENNEDY J,， EBERHART R. Particle swarm optimizat[A].Proc IEEE Int  Conf. on Neural[C]. Perth,， 1995. 1942-1948.
[7] CLERK， M. The swarm and the queen： Towards a deterministic and adaptive particle swarm optimization[A].1951-1957. 1990. Proc. CEC 1999.
[8] 林海明.對主成分分析法運用中的十個問題的解析[J].統計與決策(理論版),，2007(8)：16-18.
[9] http：//archive.ics.uci.edu/ml/index.html 1993.07.