摘 要： 提出一種新的復合型整流器拓撲結構" title="拓撲結構">拓撲結構，該整流器與傳統(tǒng)的多重化" title="多重化">多重化整流器相比,，其THD達到了電力系統(tǒng)小于5%的要求,，功率因數" title="功率因數">功率因數在0.95以上，且當其作為三電平逆變器的輸入級時,，能夠在整流側實現NPC功能,，減輕了逆變側的控制負擔，對改善三電平變頻器的性能起著重要的作用,。通過仿真驗證了拓撲結構的合理性和控制策略的正確性,。
關鍵詞： 多重化；復合型整流器,；中點箝位控制,；高功率" title="高功率">高功率因數；低諧波
?
隨著變頻技術的快速發(fā)展,，逆變技術,、PWM調制技術等相關領域都有了長足的發(fā)展,，但作為變頻器輸入級的高功率整流器等技術卻相對發(fā)展較慢[1]。目前,，多數變頻器廠商的產品中采用不控整流二重化技術，其特點是結構簡單,，成本低,，且相對于普通的不控整流結構，其交流側電流諧波有了明顯的改善[2],。但其缺點仍十分明顯,，如交流側THD仍較高、功率因數較低等,，這將直接導致電力系統(tǒng)中諧波與無功的增加[3-4],。圍繞抑制諧波電流、提高整流器的功率因數等方面,，本文提出了一種新型的復合型高功率因數整流器,，從拓撲結構、控制系統(tǒng)等幾個方面展開深入研究,，并用Matlab/Simulink進行仿真,，結果表明本文提出的新型復合型整流器拓撲結構及其控制策略能夠實現中高壓下的高功率因數和低輸入電流諧波的電能變換。
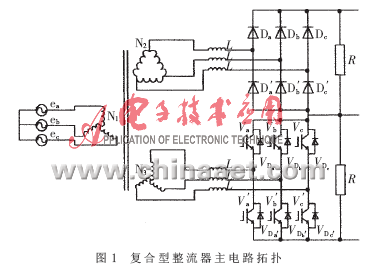
1 整流器主電路結構及工作原理
1.1 復合型整流器的拓撲結構
新的復合型高功率因數整流器由不控和可控兩部分組成,，其結構如圖1所示,。交流側接變壓器的原端A、B,、C三相,。整流變壓器為三繞組接法，原端為單繞組三相,，副端為雙繞組三相,，繞組中點有抽頭，可在應用于可控整流和不控整流中分別實現Y接法和△接法,。當二次側均為Y接法時,，可應用于復合型整流器中。繞組匝數比為
,，輸出電壓" title="輸出電壓">輸出電壓較高的繞組每相通過串聯感抗與后面的不控整流橋臂構成升壓型電路,，輸出電壓較低的繞組每相通過串聯感抗與后面的可控整流橋臂構成升壓型電路。這是由于不控整流相對于可控整流而言,，其直流電壓利用率低,，若要保證其輸出直流電壓在同一數量級，應保證不控整流有相對較高的三相交流輸入電壓,。不控整流單元采用功率二極管作為開關器件,，可控單元采用IGBT反并聯二極管作為其開關器件,。直流側，兩單元串聯后其連接點作為后續(xù)逆變電路的電位中點,，兩側直流電壓經吸收電容,、濾波電容后對負載供電。與傳統(tǒng)的相移式多重化整流拓撲一樣,，該復合型整流側拓撲中每個開關器件和功率二極管在關斷時承受的電壓都為整流輸出電壓的一半,。
?
?
1.2 復合型整流器的工作原理
復合型多重化整流器是從相移式多重化整流器發(fā)展而來的。相移多重化整流器主要通過變壓器移相實現,，變壓器輸出電壓的相移角度起到了關鍵的作用,，多重化整流器消諧性能的好壞也取決于變壓器相移角度的準確性。一旦出現偏差,，相應次數的諧波將不能完全消去,，嚴重影響相移多重化整流器的性能。特別是在采用18脈動以上的結構時,，普通變壓器很難實現分數角度的相移,，需采用變壓器的曲折接法，其實現難度更高,，精度更難于把握,。在復合型多重化整流器中，變壓器的這種作用被減弱了,，它不需要變壓器實現諧波的相移,，而是通過PWM調制技術，使得可控整流產生的諧波成分與不控整流產生的諧波成分幅值相等,，相位錯開180°,，從而達到兩單元諧波成分移相、相消的目的,。
復合型整流器的原理如圖2所示,。圖中Us表示交流電源電壓，is為電源電流,，iL1,、iL2分別為不控和可控兩個整流單元的負載電流，iC1,、iC2為不控和可控整流單元的交流側電流,。電源電流is為不控和可控整流單元的交流側電流之和再乘以變壓器變比k獲得，即is=k(iC1+iC2),。不控整流單元為非線性作為諧波源,，它產生諧波?？煽卣鲉卧饕蓛纱蟛糠纸M成,，即指令電流運算電路和補償電流發(fā)生電路(由電流跟蹤控制電路,、驅動電路和可控整流電路三部分構成)。系統(tǒng)基本工作原理是：檢測交流三相電源處的電流和電壓,，經指令電流運算電路計算得出補償電流的指令信號,，據此由補償電流發(fā)生電路產生補償電流，該補償電流與不控整流單元交流電流中要補償的諧波電流相抵消,，最終得到期望的電源電流,。
?
2 復合型整流器的控制方法
2.1 諧波的抑制
(1)諧波的檢測
目前復合型整流器主要采用的控制方法包括基于諧波檢測控制方法、基于直流側電容電壓的控制方法和單周控制方法,。本文設計的諧波檢測方法不同于上述幾種，其控制原理圖如圖3所示,。
?
在這種方法中只需要檢測網側電流,，檢測的物理量少，控制系統(tǒng)得到了簡化,。但為了保證控制的準確性,，需要利用瞬時無功理論計算其諧波含量。
設三相電路各相電壓和電流的瞬時值分別為ea,、eb,、ec和ia、ib,、ic,。由下面的變換可以得到α、β兩相瞬時電壓eα,、eβ和α,、β兩相瞬時電流iα、iβ,。
??? 
?
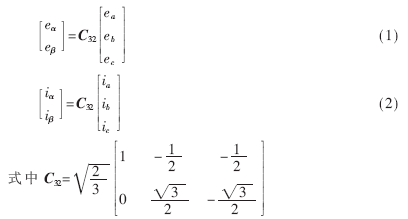矢量圖如圖4所示,，eα、eβ,、iα,、iβ分別為e、i在α,、β軸的投影,，瞬時有功電流ip和瞬時無功電流iq分別為電流矢量i在電壓矢量e及其法線上的投影，即：
??? 
?
??? 
????
????? 
?
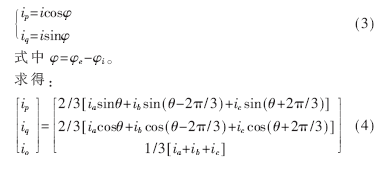其bode圖如圖5所示,。
?
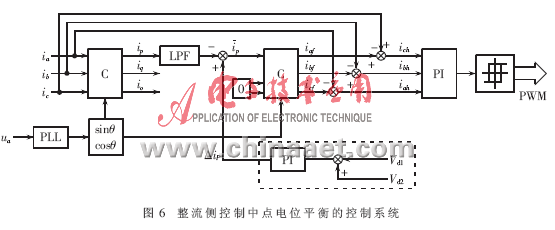
2.2 直流側中點電位控制方法
在變頻器的逆變側,，由于能量流動的不平衡性，作為逆變電路一部分的電位中點同樣受到能量流動的影響,，導致其電位不為零,。但電位中點同樣與整流側相連,，整流側的能量流動同樣會影響其電位的變化，只要這種變化趨勢能夠彌補逆變側帶來的影響,，就能保證中點電位不變或在零附近波動,。
根據復合型整流電路的特點，其不控單元整流部分的直流輸出電壓是不變且不可控的,，因此控制中點電位的唯一途徑是改變可控單元的直流輸出電壓,，使其跟蹤不控單元直流輸出電壓的變化，保持二者的相等關系,。
在整流側控制中點電位平衡的控制系統(tǒng)結構圖如圖6所示,。不控單元與可控單元的直流側電壓采樣信號經比較器比較后，經PI調節(jié)器反饋給電流內環(huán),。為保證諧波電流發(fā)生電路具有良好的補償電流跟隨性能,，必須將整流器直流側電容的電壓控制為一個適當的值。圖6指令電流運算電路中虛線框內的部分結合諧波電流發(fā)生電路實現對直流側電壓的控制,。圖中,，Vd1是可控單元直流輸出電壓的反饋量，Vd2是不控單元直流輸出電壓的反饋量,，兩者之差經 PI 調節(jié)器后得到調節(jié)信號△ip,，將它疊加到瞬時有功電流的直流分量ip上，這樣經運算在指令信號ich中就包含了一定的基波有功電流,。諧波電流發(fā)生電路根據ich產生補償電流iL注入電網,，使得可控整流單元的補償電流中包含一定的基波有功電流分量，從而使可控整流單元交流側電流補償不控整流單元交流側電流后,，仍然能夠有足夠的能量流動到直流側,，保持與不控整流單元直流電壓的平衡關系。
?
3 仿真及實驗結果
將復合型整流器與傳統(tǒng)的相移式多重化整流器的仿真結果作對比,，其交流側電流頻譜如圖7,、圖8所示。
?
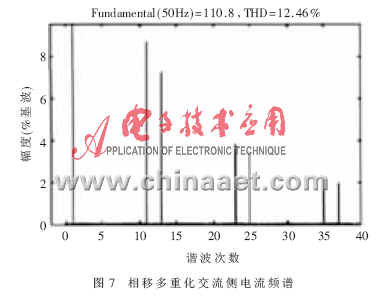
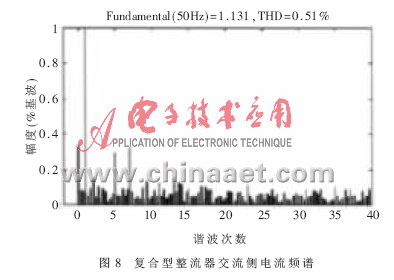
由圖可見,，普通的相移式多重化整流器中,，其交流側電流諧波含量仍然較高，為12.46%,，其諧波主要為6k±1(k=1,，2，3…)次,，且11,、13 次諧波含量較高，占基波成分的8%左右,。而新型復合型整流器的交流側諧波含量明顯降低,，為0.51%,，可以滿足電力系統(tǒng)對諧波小于5%的要求，且各次諧波含量都較小,，比例較大的5,、7 次諧波含量也僅為基波的0.3%左右。
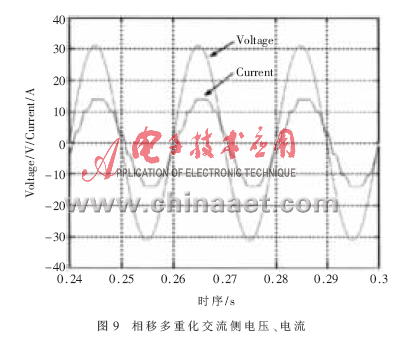
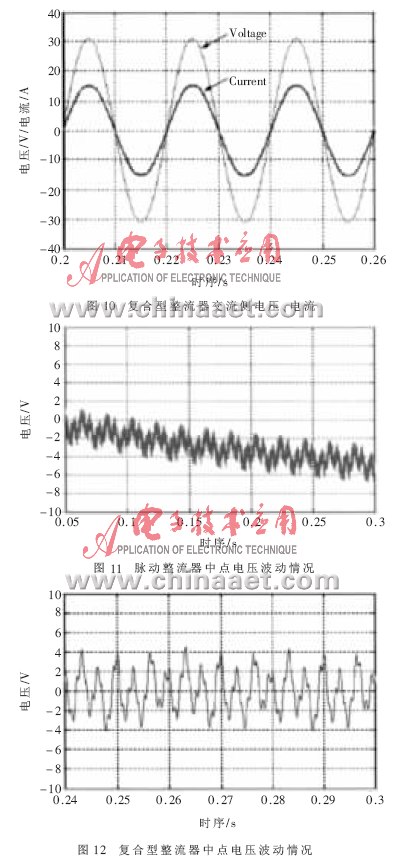
新型高功率復合型整流器與傳統(tǒng)的相移式多重化結構在功率因數方面的對比如圖9,、圖10所示,。
?
?
可見，普通相移式多重化整流器由于沒有進行閉環(huán)控制,，所以不可能工作在單位功率因數下,，且隨著負載及主電路參數的變化，其功率因數也會隨之改變,。而新型的復合型整流器功率因數接近1,，且當負載及主電路的參數改變后其功率因數仍然能保證為1。
在逆變側,，采用SVPWM控制方法,，但不對中點電位進行控制,，當采用相移二重化整流器供電時,，其中點電位波形如圖11所示。此時由于大小矢量對中點電位的作用效果不同,，中點電壓變化較大,，遠離零電平。
當采用復合型多重化整流器供電時,，其中點電位波形如圖12所示,。此時通過在整流側采用中點電位控制，中點電壓在零附近波動,，達到了控制中點電位平衡的要求,。
?
本文提出了一種復合型高功率因數整流器的拓撲結構，對該拓撲結構的工作原理進行了分析,，并給出了諧波抑制以及中點電位平衡等問題的控制策略,，仿真驗證了結論的正確性。
參考文獻
[1] 徐甫榮.中高壓變頻器主電路拓撲結構的分析比較.電氣傳動自動化,，2004,，25(4)：5-12.
[2] 翁利民，陳允平,，吳軼群.配電網的諧波源特性與高次諧波的抑制.電力電容器,，2001，(4)：10-14.
[3] 呂潤馀,，段曉波.多脈動整流電路諧波統(tǒng)一分析——12/18/24/30/36/48脈動整流系統(tǒng)諧波分析.河北電力技術,，2003,，22(7)：1-8.
[4] MINO K，GONG G,，KOLAR J W.Novel hybrid 12-pulse?line interphase transformer boost-type rectifier with?
controlled output voltage.in：Power Electronics and Motion?Control Conference,，IPEMC 2004.2004：924-931.
[5] SUJITJORN S，AREERAK K L,，KULWORAWANICHPONG?K.The DQ axis with Fourier(DQF) method for harmonic?
identification.IEEE Transactions on Power Delivery,，2007，22(1)：737-739.
[6] 趙小英.基于DSP芯片的有源電力濾波器數字控制系統(tǒng)研究.中國科學院碩士學位論文,，2005.
[7] 楊漢生,，李明，楊成梧.設計數字式巴特沃茲濾波器的新方法.電測與儀表,，2006,，43(484)：37-38.
[8] 陳立功.一種基于TMS320F2812的數字濾波器的快速設計方法.國外電子測量技術，2005,，8(126)：12-13.