0 引言
電力系統(tǒng)負(fù)荷預(yù)測(cè)是電網(wǎng)能量管理系統(tǒng)的重要內(nèi)容,通過精確的負(fù)荷預(yù)測(cè),可以經(jīng)濟(jì)合理地安排機(jī)組啟停,減少旋轉(zhuǎn)備用容量,合理安排檢修計(jì)劃,降低發(fā)電成本,提高經(jīng)濟(jì)效益。常用的方法有非線性回歸、神經(jīng)網(wǎng)絡(luò)法、時(shí)間序列法、模糊理論等。非線性回歸和時(shí)間序列法在電網(wǎng)情況正常、生產(chǎn)和氣象變化不大的時(shí)候預(yù)測(cè)效果良好,但不能考慮一些影響負(fù)荷的要素,如休息日、氣象等,當(dāng)這些因素發(fā)生突變時(shí)預(yù)測(cè)精度受到影響。神經(jīng)網(wǎng)絡(luò)和模糊理論考慮到了影響負(fù)荷的一些不確定因素,但沒有徹底解決網(wǎng)絡(luò)結(jié)構(gòu)設(shè)計(jì)的難題,且需要較長的訓(xùn)練時(shí)間。
SVM(支持向量機(jī)" title="支持向量機(jī)">支持向量機(jī))是由Vapnik[1]最早提出的一種統(tǒng)計(jì)學(xué)習(xí)方法,近年來已經(jīng)被成功地應(yīng)用于語音識(shí)別、文字識(shí)別、時(shí)序數(shù)列預(yù)測(cè)等領(lǐng)域。研究顯示,該統(tǒng)計(jì)學(xué)習(xí)方法具有學(xué)習(xí)速度快、全局最優(yōu)和推廣能力強(qiáng)的優(yōu)點(diǎn),其學(xué)習(xí)結(jié)果經(jīng)常明顯好于其它的模式識(shí)別和回歸預(yù)測(cè)方法。本文將SVM理論應(yīng)用于電力系統(tǒng)短期負(fù)荷預(yù)測(cè)" title="短期負(fù)荷預(yù)測(cè)">短期負(fù)荷預(yù)測(cè),既考慮了影響負(fù)荷的諸因素,又建立了完善的數(shù)學(xué)模型。
SVM算法對(duì)與預(yù)測(cè)負(fù)荷曲線較平滑的系統(tǒng),能夠取得較理想的效果。但是,對(duì)于慣性較小、隨機(jī)波動(dòng)性較強(qiáng)的中小型電網(wǎng),其效果相對(duì)較差。改進(jìn)的方法是,先采用Fourier算法將歷史負(fù)荷曲線分解為平滑曲線和隨機(jī)波動(dòng)曲線兩部分,只采用平滑部分作為SVM的歷史訓(xùn)練數(shù)據(jù),能夠取得更好的效果。
1 SVM線性回歸模型
假設(shè)有一組訓(xùn)練數(shù)據(jù),共有l(wèi)個(gè),其中第i個(gè)數(shù)據(jù)包含變量和與之相對(duì)應(yīng)的變量xi∈Rn和與之相對(duì)應(yīng)的變量yi∈R,SVM定義了一種機(jī)器(machine),用于確定x到y(tǒng)的映射關(guān)系x→f(X,a),a為可調(diào)參數(shù),通過對(duì)已知數(shù)據(jù)的學(xué)習(xí)來確定它。在線性回歸中,定義映射函數(shù)f(x)=
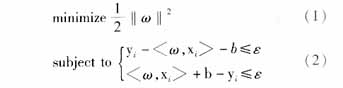
滿足(2)式有時(shí)候會(huì)使問題的求解變得非常困難,可以通過在目標(biāo)函數(shù)中增加損失函數(shù)" title="損失函數(shù)">損失函數(shù)來進(jìn)行處理,損失函數(shù)有多種形式,本文中只考慮ε-intensive損失函數(shù):

式中C為常數(shù),是回歸精度超過允許值的懲罰因子。(4)為有條件約束的優(yōu)化問題,根據(jù)非線性規(guī)劃對(duì)偶性理論,對(duì)其建立沒有約束條件的Lagrange方程,并將最小值問題它轉(zhuǎn)化為對(duì)偶的最大值問題:
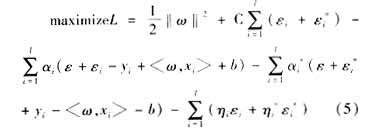
2 非線性回歸模型及其核函數(shù)" title="核函數(shù)">核函數(shù)
當(dāng)然,現(xiàn)實(shí)中的大部分問題并不是簡單的線性問題,對(duì)非線性問題進(jìn)行回歸,可以通過映射φ:X→τ把xi映射到特征空間τ,然后用核函數(shù)k(x,x′)=<φ(x),φ(x′)>來代替線性回歸中的
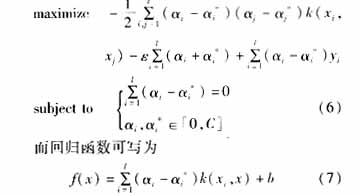
無論線性和非線性模型,都可采用內(nèi)點(diǎn)法求解。
3 短期負(fù)荷預(yù)測(cè)的SVM與Fourier方法
3.1 樣本及其輸入輸出量的選擇
本文采用SVM方法來解決短期負(fù)荷預(yù)測(cè)問題。對(duì)于訓(xùn)練樣本,首先通過聚類找出和預(yù)測(cè)點(diǎn)在星期屬性、節(jié)假日屬性、預(yù)測(cè)時(shí)段都相同的數(shù)據(jù)作為SVM中的y值,相應(yīng)的x值(即樣本輸入量)分為如下幾類:
1)A={a1,a2,...,an} ,預(yù)測(cè)日之前n日內(nèi)的在預(yù)測(cè)時(shí)段的負(fù)荷數(shù)據(jù)
2)B={b1,b2,...,bm},預(yù)測(cè)日前一日預(yù)測(cè)時(shí)段之前m個(gè)時(shí)段的負(fù)荷數(shù)據(jù)
3)C={c1,c2,...,cs},預(yù)測(cè)日的氣象預(yù)報(bào),共s個(gè)數(shù)據(jù),包含平均氣溫、最高氣溫、最低氣溫、風(fēng)力、濕度等
4)D={d1,d2,...,dn} ,預(yù)測(cè)日之前日內(nèi)的每日氣象數(shù)據(jù),其中任何一個(gè)元素di包含s個(gè)如上所述的氣象數(shù)據(jù)
5)E={e1,e2,...,e7} ,預(yù)測(cè)日的周屬性,代表周一到周日,每個(gè)變量用1或0來表示
6)F ,一些從已知變量中通過某種計(jì)算演化而來的、對(duì)負(fù)荷的結(jié)果可能影響較大的數(shù)據(jù)(例如前一日溫度與該日預(yù)測(cè)溫度的差值、前二日與前一日在預(yù)測(cè)時(shí)段的負(fù)荷差值、該日前一周每天在預(yù)測(cè)時(shí)段的負(fù)荷平均值等)。
3.2 負(fù)荷預(yù)測(cè)的支持向量機(jī)模型
為了選擇合適的核函數(shù),本文使用線性函數(shù)、多項(xiàng)式函數(shù)、徑向基函數(shù)、對(duì)數(shù)S型等多種核函數(shù)進(jìn)行測(cè)試,發(fā)現(xiàn)徑向基函數(shù)的模型對(duì)于負(fù)荷預(yù)測(cè)問題精度最高,因此本文選用徑向基函數(shù)作為核函數(shù)。
假設(shè)按照上述樣本及其輸入輸出量的選擇構(gòu)造的l個(gè)樣本集合為{(xi,yi),i=1,2,...,l},則負(fù)荷預(yù)測(cè)的支持向量機(jī)模型可寫為式(6)的形式,其中![]() 為徑向基函數(shù)。
為徑向基函數(shù)。
3.3 Fourier算法對(duì)歷史數(shù)據(jù)進(jìn)行平滑處理
經(jīng)數(shù)字實(shí)驗(yàn)證明,上述短期負(fù)荷預(yù)測(cè)的SVM方法對(duì)于負(fù)荷慣性較大的大型電網(wǎng)有較理想的效果,但是,如果將它應(yīng)用于具有較多沖擊性負(fù)荷(如軋鋼廠),其誤差較大。為了改進(jìn)算法的預(yù)測(cè)效果,本文提出用Fourier算法對(duì)每日歷史負(fù)荷曲線進(jìn)行Fourier變換,分解為平滑曲線和隨機(jī)波動(dòng)曲線兩部分,只采用平滑部分作為歷史訓(xùn)練數(shù)據(jù),方法如下。
1) 對(duì)欲進(jìn)行處理的一日負(fù)荷數(shù)據(jù),檢驗(yàn)其初始點(diǎn)負(fù)荷f(0)與終點(diǎn)負(fù)荷f(24)的差值是否小于給定的閾值δ。如果是, 說明該曲線基本滿足Fourier分解的基本條件f(0)=f(T);否則,進(jìn)行時(shí)間軸的旋轉(zhuǎn)變換,使得f(0)=f(T);
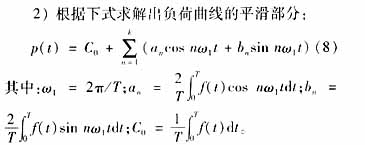
如果未經(jīng)坐標(biāo)軸變換,T取24(小時(shí));否則,取坐標(biāo)變換后的時(shí)間軸對(duì)應(yīng)初始負(fù)荷點(diǎn)與終點(diǎn)的坐標(biāo)差值。
k的取值視電網(wǎng)負(fù)荷曲線的波動(dòng)情況而定。取值應(yīng)越大,擬合效果越好,但是其濾波作用越差。經(jīng)過數(shù)字實(shí)驗(yàn)發(fā)現(xiàn),k取15對(duì)波動(dòng)性較大的地區(qū)性電網(wǎng)能有較理想的濾波效果且與原曲線擬合較好。
3) 如果經(jīng)過了坐標(biāo)軸變換,將數(shù)據(jù)再還原到原始時(shí)間坐標(biāo)軸。
4 計(jì)算結(jié)果與誤差
本文采用的算例是根據(jù)由常州電力公司提供的2003年3月1日至4月24日的每天氣溫?cái)?shù)據(jù)和每天288點(diǎn)的負(fù)荷數(shù)據(jù),預(yù)測(cè)4月25日全天96點(diǎn)的數(shù)據(jù)。為了考察本文所使用的方法的精度,還采用BP神經(jīng)網(wǎng)絡(luò)法和SVM算法(無Fourier分解)進(jìn)行了預(yù)測(cè)。圖1到圖3分別示出三種方法的該日的預(yù)測(cè)情況。
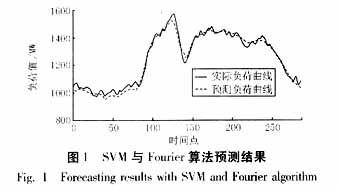
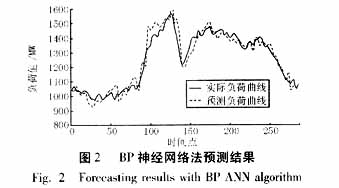

本文所提出的算法計(jì)算的該日的最大相對(duì)誤差(絕對(duì)值)為5.2%,平均誤差為2.4%。對(duì)比神經(jīng)網(wǎng)絡(luò)法(平均誤差4.1%,最大相對(duì)誤差11.9%)和單純SVM算法(平均誤差3.7%,最大誤差10.1%)的誤差結(jié)果,該法具有較高的精度。本文所提算法對(duì)每個(gè)點(diǎn)進(jìn)行預(yù)測(cè),訓(xùn)練程序運(yùn)行時(shí)間都在400毫秒到1500毫秒之間(含濾波時(shí)間),測(cè)試時(shí)間則小于20毫秒,具有較快的速度。
5 結(jié)論
本文介紹了SVM和Fourier算法及其在電力系統(tǒng)短期負(fù)荷預(yù)測(cè)中的應(yīng)用。算法考慮到影響負(fù)荷的要素,對(duì)歷史數(shù)據(jù)聚類,找出與預(yù)測(cè)點(diǎn)屬同一類的數(shù)據(jù)進(jìn)行訓(xùn)練。Fourier算法將負(fù)荷曲線平滑化,防止了隨機(jī)波動(dòng)對(duì)預(yù)測(cè)的干擾。算例證明,該方法結(jié)果合理,運(yùn)行速度快,精度很高,是一種很有應(yīng)用價(jià)值的新興算法。

